ПЛАН
Чтения лекции №7
по дисциплине Теория статистики
Тема: « Корреляционная связь и ее статистическое изучение »
(наименование темы)
Цельзанятия: ознакомить студентов сстатистическими методами выявления наличия корреляционной связи, показателями степени тесноты корреляционной связи.Дать п онятие о регрессионном анализе и его применении в практике.
Литература по теме:
1. а) основная __1. Елисеева И.И. Статистика. – М., 2010.
2. Ефимова М .Р. и др. Практикум по общей теории статистики: Учебное пособие / М.Р. Ефимова, О.И. Гончаренко, Е.В. Петрова – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А. Теория статистики. – М.: Финансы и статистика, 2009.
| №№ п.п. | Содержание занятия | Отводимое учебное время, мин. | Применяемые наглядные пособия и ТСО |
| Организационная часть - проверить наличие студентов* Вводная часть (вступительное слово) - кратко напомнить материал предыдущего занятия; - объявить тему лекции; - довести учебные вопросы; - определить место темы в учебном курсе, указать связь с предыдущими темами и междисциплинарные связи; - отметить актуальность темы и ее практическое значение; - довести цель занятия; - сообщить литературныеисточники по теме занятия. | |||
| Основная часть (учебные вопросы) Излагаются вопросы (проблемы), изучаемые на лекции: 1.Понятие корреляционной связи. 2.Методы установления факта наличия и направлениякорреляционной зависимости. 3.Методы оценки тесноты связи и её существенности. 4.Построение парной модели связи и оценка её качества. 5. Множественная корреляция, задачи ее изучения. Парные и частные коэффициенты корреляции, их значение. Отбор факторов для включения в уравнение регрессии. | PowerPoint | ||
| Заключительная часть - сделать выводы по теме лекции; - ответить на вопросы студентов; - дать задание на самостоятельную работу; - объявить тему следующего занятия. |
Преподаватель: профессор Новиков В.В. _______
(должность, подпись, инициалы, фамилия)
«30» августа 2012 г.
Кафедра таможенной статистики
УТВЕРЖДАЮ
Заведующая кафедрой
Н.В. Ширкунова
ЛЕКЦИЯ № 7
на тему: « Корреляционная связь и ее статистическое изучение »
Дисциплина: Теория статистики
Автор: к.т.н., с.н.с. Новиков В.В.
Москва
Лекция № 7
Корреляционная связь и ее статистическое изучение
Корреляционная связь — связь, проявляющаяся не в каждом отдельном случае, а в массе случаев в средних величинах в форме тенденции.
Статистическое исследование корреляционной связи ставит своей конечной целью получение модели зависимости для ее практического использования. Решение этой задачи осуществляется в следующей последовательности.
1. Логический анализ сущности изучаемого явления и причинно- следственных связей. В результате устанавливаются результативный показатель (y) и факторы его изменения, характеризуемые показателями (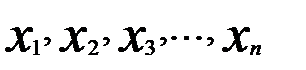 ). Связь двух признаков (у и х) называется парной корреляцией. Влияние нескольких факторов на результативный признак называется множественной корреляцией.
). Связь двух признаков (у и х) называется парной корреляцией. Влияние нескольких факторов на результативный признак называется множественной корреляцией.
По общему направлению связи могут быть прямые и обратные. При прямых связях с увеличением признака х увеличивается и признак у, при обратных — с увеличением признака х признак у уменьшается.
2. Сбор первичной информации и проверка ее на однородность и нормальность распределения. Важнейшими условиями правильного применения методов корреляционного анализа являются: достаточное число наблюдений, однородность тех единиц, которые подвергаются изучению, распределение исследуемых признаков факторов в соответствии с законом нормального распределения.
Для оценки однородности совокупности используется коэффициент вариации по факторным признакам:
 , (7.1)
, (7.1)
где  — среднее значение признака-фактора;
— среднее значение признака-фактора;
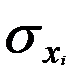 — среднее квадратическое отклонение признака-фактора.
— среднее квадратическое отклонение признака-фактора.
Для рассматриваемой задачи (см. табл. 5.2 л.5) 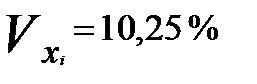 следовательно, совокупность считается является однородной, т.к. коэффициент её вариации не превышает 33%.
следовательно, совокупность считается является однородной, т.к. коэффициент её вариации не превышает 33%.
Проверка нормальности распределения исследуемых факторных признаков может выполняться двумя способами:
1) построить теоретическую кривую нормального распределения и проверить близость теоретического и эмпирического распределений с помощью критерия согласия;
2) использовать систему неравенств:
 , (7.2)
, (7.2)
где 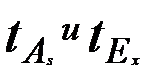 - относительные показатели асимметрии и эксцесса соответственно (см. л. 5), т.е. эмпирическое распределение не противоречит нормальному.
- относительные показатели асимметрии и эксцесса соответственно (см. л. 5), т.е. эмпирическое распределение не противоречит нормальному.
3. Исключение из массива первичной информации всех резко выделяющихся (аномальных) единиц по уровню признаков-факторов.
Если исходные данные являются эмпирическими, то их необходимо проверить на наличие аномальных наблюдений (резко выделяющихся единиц совокупности):
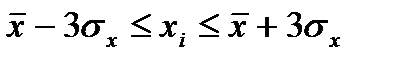 или
или  (7.3)
(7.3)
 , (7.4)
, (7.4)
Если условия (7.3) или (7.4) не выполняются, то соответствующие единицы совокупности исключаются из дальнейшего рассмотрения, а затем формируется новый массив для последующего анализа.
4. Установление факта наличия и направления корреляционной зависимости между результативным (у) и факторным (х) признаками. Для установления наличия корреляционной связи используется ряд специфических методов: параллельное сопоставление рядов результативного и факторного признака, графическое изображение фактических данных с помощью поля корреляции, построение корреляционной таблицы, построение групповой таблицы.
Сопоставление двух параллельных рядов — простейший метод обнаружения связи. Значения факторного признака располагают в возрастающем порядке в первом ряду; во втором ряду записывают соответствующие значения результативного признака (т.е. значения, относящиеся к той же единице); затем прослеживается направление изменения результативного признака (см. табл.5.2, л.5)
Корреляционное поле — точечный график, для построения которого по масштабной оси абсцисс откладываются значения факторного признака х, а по масштабной оси ординат — значения результативного признака у. Каждой единице изучаемой совокупности на графике соответствует одна точка, положение которой определяется величиной двух признаков, характеризующих эту единицу. По расположению точек судят о наличии связи или ее отсутствии. Если точки разбросаны по всему полю — связи нет.
На рис.7.1 приведено корреляционное поле, построенное по данным табл.5.2, которое свидетельствует о наличии прямой связи близкой к линейной.
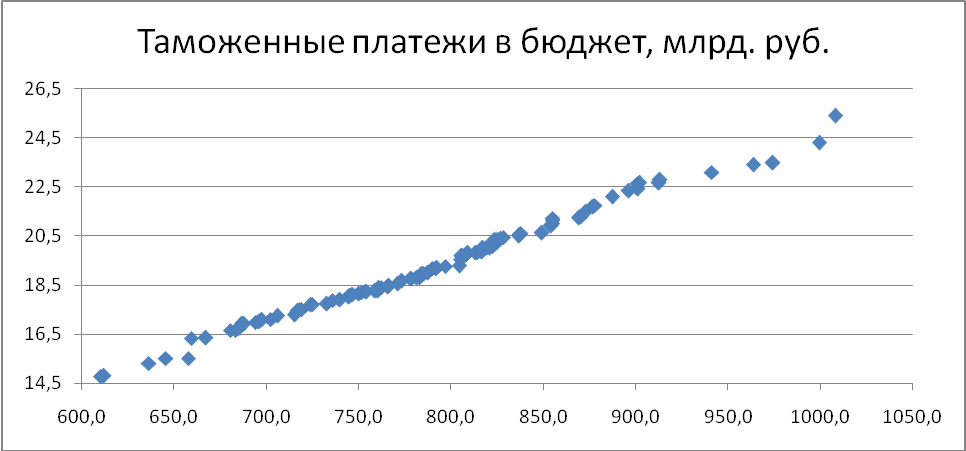
Рис.7.1 Таможенные платежи в бюджет в функции ВТО фирм
В тех случаях, когда количество единиц, входящих в изучаемую совокупность, относительно велико, возникает необходимость сведения данных в особую таблицу, которая называется корреляционной таблицей. Для построения корреляционной таблицы проводится группировка значений факторного и результативного признака при одинаковом числе групп. В таблице факторный признак x располагают в строках, а результативный признак у — в столбцах (графах) таблицы. В клетки, образованные пересечением строк и столбцов таблицы, записываются частоты повторения данного сочетания значений х и у. Если частоты расположены в клетках по диагонали из левого верхнего угла в правый нижний угол, то можно предполагать о наличии прямой корреляционной зависимости между признаками. Если частоты расположены в клетках по диагонали справа налево (из правого верхнего угла в левый нижний угол), то предполагают наличие обратной связи.
Основным методом выявления наличия корреляционной связи является метод аналитической группировки и определения групповых средних. Он заключается в том, что все единицы совокупности разбиваются на группы по величине признака-фактора и для каждой группы определяется средняя величина результативного признака (см. графы 2 и 13 табл. 5.2). На основе данных аналитической группировки строится график эмпирической линии связи (линии регрессии), вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о форме корреляционной связи. Если эмпирическая линия связи по своему виду приближается к прямой линии, то можно предположить наличие прямолинейной корреляционной связи; если эмпирическая линия приближается к какой-либо кривой, то это связано с наличием криволинейной связи.
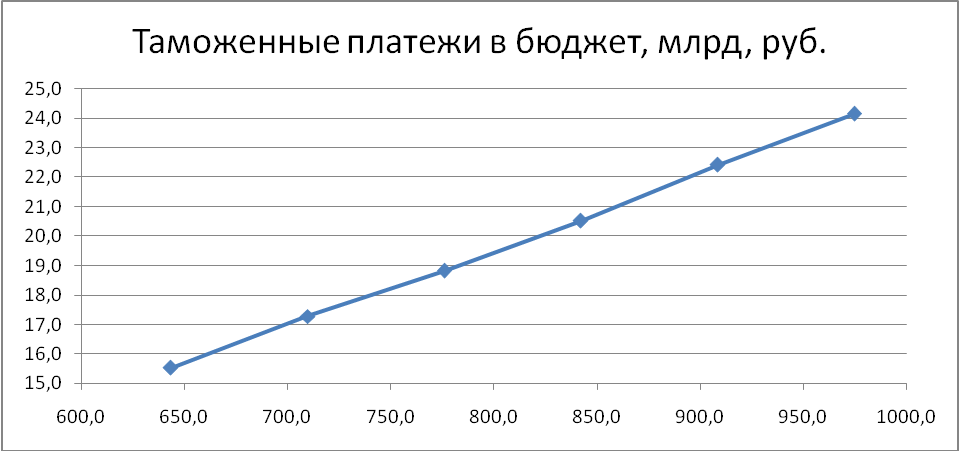
Рис.7.2 Зависимость величины средних таможенных платежей от средних значений ВТО в группах фирм
5. После установления факта наличия связи и ее формы измеряется степень тесноты связи и проводится оценка ее существенности. Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции ( ); при любой форме зависимости (линейной и криволинейной) — эмпирическое корреляционное отношение (
); при любой форме зависимости (линейной и криволинейной) — эмпирическое корреляционное отношение ( )).
)).
Для расчета линейного коэффициента корреляции можно использовать формулу:
 , (7.5)
, (7.5)
где  — среднее значение произведения факторного и результативного признаков;
— среднее значение произведения факторного и результативного признаков;
 - средние значения факторного и результативного признаков;
- средние значения факторного и результативного признаков;
n — число единиц в совокупности;
 — средние квадратические отклонения соответственно признака - фактора и результативного признака.
— средние квадратические отклонения соответственно признака - фактора и результативного признака.
Линейный коэффициент корреляции может принимать значения в пределах от —1 до +1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак при нем указывает направление связи: знак «+» соответствует прямой зависимости, знак «—» — обратной.
Если коэффициент корреляции равен нулю, то связи между признаками нет; если он равен единице (с любым знаком), то между признаками существует функциональная связь.
Оценка существенности линейного коэффициента корреляции при большом объеме выборки (свыше 500) проводится с использованием отношения коэффициента корреляции ( ) к его средней квадратической ошибке (
) к его средней квадратической ошибке ( ):
):
 , (7.6)
, (7.6)
где  . (7.7)
. (7.7)
Если это отношение окажется больше значения t -критерия Стьюдента, определяемого по приложению 6 при числе степеней свободы к = п — 2 и с вероятностью (1 —  ), то следует говорить о существенности коэффициента корреляции (
), то следует говорить о существенности коэффициента корреляции (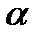 — уровень значимости 0,01 или 0,05).
— уровень значимости 0,01 или 0,05).
При недостаточно большом объеме выборки величину средней квадратической ошибки коэффициента корреляции определяют по формуле
 . (7.8)
. (7.8)
В этом случае 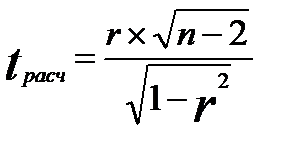 . (7.9)
. (7.9)
Полученная величина  сравнивается с табличным значением t -критерия Стьюдента.
сравнивается с табличным значением t -критерия Стьюдента.
В тех случаях, когда  получен по данным малой выборки и близок к единице (
получен по данным малой выборки и близок к единице ( > 0,8), для проверки его существенности целесообразно использовать метод преобразованной корреляции, предложенный Р. Фишером.
> 0,8), для проверки его существенности целесообразно использовать метод преобразованной корреляции, предложенный Р. Фишером.
Средняя квадратическая ошибка Z'-распределения зависит только от объема выборки и определяется по формуле
 . (7.10)
. (7.10)
По таблице соотношений между  и Z' (приложение 9) находят значение Z', соответствующее рассчитанному коэффициенту корреляции.
и Z' (приложение 9) находят значение Z', соответствующее рассчитанному коэффициенту корреляции.
Если соотношение Z' к средней квадратической ошибке (Z':  ) окажется больше табличного значения критерия Стьюдента при определенном уровне значимости, то можно говорить о наличии связи между признаками в генеральной совокупности.
) окажется больше табличного значения критерия Стьюдента при определенном уровне значимости, то можно говорить о наличии связи между признаками в генеральной совокупности.
Корреляционное отношение определяется по формулам:
 , (7.11)
, (7.11)
где 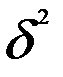 — межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора;
— межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора;
 - общая дисперсия результативного признака; т
- общая дисперсия результативного признака; т
 — средняя внутригрупповая дисперсия результативного признака.
— средняя внутригрупповая дисперсия результативного признака.
Вычисление корреляционного отношения требует достаточно большого объема информации, которая должна быть представлена в форме групповой таблицы или в форме корреляционной таблицы, т. е. обязательным условием является группировка данных по признаку-фактору. Изменяется корреляционное отношение от 0 до 1.
При недостаточном количестве данных в выделенных группах к рассчитанной величине корреляционного отношения вносится поправка:
 , (7.12)
, (7.12)
где m — число выделенных групп.
Корреляционное отношение в квадрате (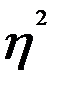 ) называют коэффициентом детерминации (причинности), он отражает долю факторной дисперсии в общей дисперсии.
) называют коэффициентом детерминации (причинности), он отражает долю факторной дисперсии в общей дисперсии.
В практике могут быть использованы и другие показатели для определения степени тесноты связи.
Элементарной характеристикой степени тесноты связи является коэффициент Фехнера:
 , (7.13)
, (7.13)
где  — количество совпадений знаков отклонений индивидуальных величин факторного признака х и результативного признака у от их средней арифметической величины (например, «плюс» и «плюс», «минус» и «минус», «отсутствие отклонения» и «отсутствие отклонения»);
— количество совпадений знаков отклонений индивидуальных величин факторного признака х и результативного признака у от их средней арифметической величины (например, «плюс» и «плюс», «минус» и «минус», «отсутствие отклонения» и «отсутствие отклонения»);
 — количество несовпадений знаков отклонений индивидуальных значений изучаемых признаков от значения их средней арифметической.
— количество несовпадений знаков отклонений индивидуальных значений изучаемых признаков от значения их средней арифметической.
Коэффициент Фехнера целесообразно использовать для установления факта наличия связи при небольшом объеме исходной информации. Он изменяется в пределах — 1,0 <Кф< + 1,0.
Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что значения этих признаков могут быть проранжированы по степени убывания или возрастания, используется коэффициент корреляции рангов Спирмена или коэффициент корреляции рангов Кендэла.
Коэффициент корреляции рангов Спирмена определяется по формуле
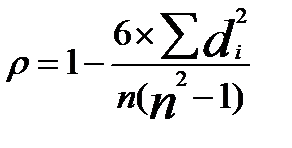 , (7.14)
, (7.14)
где  — разность между величинами рангов признака-фактора и результативного признака;
— разность между величинами рангов признака-фактора и результативного признака;
п — число показателей (рангов) изучаемого ряда (соответствует числу данных).
Он варьирует в пределах от -1,0 до +1,0.
Ранговый коэффициент обычно исчисляется на основе небольшого объема исходной информации, поэтому необходимо выполнить проверку его существенности. В приложении 7 приводится таблица предельных значений коэффициента корреляции рангов Спирмена при условии верности нулевой гипотезы об отсутствии корреляционной связи ппи заданном уровне значимости и определенном объеме выборочных данных.
Если полученное значение  превышает критическую величину при данном уровне значимости, то нулевая гипотеза может быть отвергнута, т. е. величина
превышает критическую величину при данном уровне значимости, то нулевая гипотеза может быть отвергнута, т. е. величина  не является результатом случайных совпадений рангов.
не является результатом случайных совпадений рангов.
Коэффициент корреляции рангов Кендэла определяется по формуле
 , (7.15)
, (7.15)
где  ;
;
Р — сумма чисел, вычисленных для каждого ранга признака y как число последующих рангов, больших по своей величине, чем взятый ранг;
Q — сумма чисел, вычисленных для каждого ранга признака у как число последующих рангов, меньших по своей величине, чем взятый ранг (эти числа берутся со знаком минус).
Этот коэффициент изменяется в интервале от —1,0 до +1,0.
Для вычисления  сначала ранжируют ряд значений признака х, располагая их в порядке возрастания, приведя его к ряду натуральных чисел. Затем рассматривают последовательность рангов переменной у; против ранга х записывают соответствующий ему ранг у. Результаты оформляют в табличной форме. Ниже приведен ее пример.
сначала ранжируют ряд значений признака х, располагая их в порядке возрастания, приведя его к ряду натуральных чисел. Затем рассматривают последовательность рангов переменной у; против ранга х записывают соответствующий ему ранг у. Результаты оформляют в табличной форме. Ниже приведен ее пример.
| Ранг признака фактора (x) | |||||||
| Ранг результативного признака (y) |
На основе приведенных данных рассчитывают коэффициент корреляции рангов.
P = 0 + 0+1+0 + 0 + 0 +1 (число рангов, превышающих ранг 7, равно 0, ранг 6 - равно 0, ранг 4 - 1 и т.д.).
Q = (-6) + (-5) + (-3) + (-3) + (-2) + (-1) = -20
S = Р + Q =1 + (-20) = -19;
 . (7.16)
. (7.16)
Полученный коэффициент означает высокую степень обратной связи.
Для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла или коэффициент контингенции К. Пирсона.
Расчетная таблица в этом случае состоит из четырех ячеек (таблица «четырех полей»), статистическое сказуемое которой схематически может быть представлено в следующем виде (табл. 7.2):
Таблица 7.2
| Признак | А (да) |  (нет) (нет)
| Итого |
| В (да) | a | b | a+b |
 (нет) (нет)
| c | d | c+d |
| Итого | a+c | b+d | n |
В расчетной таблице:
а, b,c,d — частоты взаимного сочетания (комбинации) двух альтернативных признаков — А —  и В —
и В —  ;
;
п — общая сумма частот.
Коэффициент ассоциации исчисляется по формуле
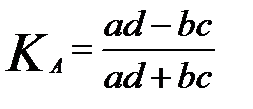 . (7.17)
. (7.17)
Коэффициент контингенции:
 , (7.18)
, (7.18)
где a, b,c,d — числа в четырехклеточной таблице.
Коэффициент контингенции также изменяется от —1 до +1, но всегда его величина для тех же данных меньше коэффициента ассоциации.
Для оценки тесноты связи между альтернативными признаками, принимающими любое число вариантов значений, применяется коэффициент взаимной сопряженности К. Пирсона и коэффицент взаимной сопряженности А. А. Чупрова.
Первичная статистическая информация для исследования этой связи располагается в форме таблицы (табл. 7.3).
Таблица 7.3
| Признак | A | B | C | Итого |
| D | 
| 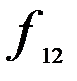
| 
| 
|
| E | 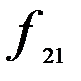
| 
| 
| 
|
| F | 
| 
| 
| 
|
| Итого | 
| 
| 
| n |
Здесь  - частоты взаимного сочетания двух атрибутивных признаков;
- частоты взаимного сочетания двух атрибутивных признаков;
п — число пар наблюдений.
Коэффициент взаимной сопряженности К. Пирсона определяется по формуле
 , (7.19)
, (7.19)
где  — показатель средней квадратической сопряженности.
— показатель средней квадратической сопряженности.
Показатель  определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки, уменьшенная на единицу:
определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки, уменьшенная на единицу:
 , (7.20)
, (7.20)
где  — частоты каждой клетки;
— частоты каждой клетки;
 — номер строки;
— номер строки;
 — итоговые частоты по строкам;
— итоговые частоты по строкам;
 — итоговые частоты по графам.
— итоговые частоты по графам.
Коэффициент взаимной сопряженности А. А. Чупрова исчисляется по формуле
 , (7.21)
, (7.21)
где  - имеет одинаковое значение с показателем
- имеет одинаковое значение с показателем 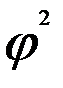 Пирсона и является показателем взаимной сопряженности;
Пирсона и является показателем взаимной сопряженности;
 — число групп по столбцам таблицы;
— число групп по столбцам таблицы;
 — число групп по строкам таблицы.
— число групп по строкам таблицы.
Коэффициент взаимной сопряженности Чупрова (К) является более гибким, поскольку он учитывает число образуемых по каждому признаку групп ( ) и
) и  ), поэтому результат является более точным по сравнению с коэффициентом взаимной сопряженности по формуле Пирсона.
), поэтому результат является более точным по сравнению с коэффициентом взаимной сопряженности по формуле Пирсона.
Коэффициент взаимной сопряженности изменяется от 0 до 1.
6. После установления достаточной степени тесноты связи выполняется построение модели связи (уравнения регрессии).
Тип модели выбирается на основе сочетания теоретического анализа и исследования эмпирических данных посредством построения эмпирической линии регрессии. Чаще всего используются следующие типы функций:
• линейная —  ;
;
• гиперболическая —  ;
;
• параболическая —  ;
;
• показательная —  .
.
Для проверки возможности использования линейной функции определяется разность ( ); если она менее 0,1, то считается возможным применение линейной функции. Для решения этой же задачи можно использовать величину
); если она менее 0,1, то считается возможным применение линейной функции. Для решения этой же задачи можно использовать величину  , определяемую по формуле
, определяемую по формуле
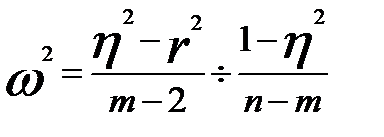 , (7.22)
, (7.22)
где m — число групп, на которое разделен диапазон значений факторного признака.
Если  окажется меньше табличного значения F -критерия, то нулевая гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается. Значение F -критерия определяется по таблице в зависимости от уровня значимости
окажется меньше табличного значения F -критерия, то нулевая гипотеза о возможности использования в качестве уравнения регрессии линейной функции не опровергается. Значение F -критерия определяется по таблице в зависимости от уровня значимости  = 0,05 (вероятность Р = 0,95) и числа степеней свободы числителя (
= 0,05 (вероятность Р = 0,95) и числа степеней свободы числителя ( ) и знаменателя (
) и знаменателя ( ) (см. приложение 5).
) (см. приложение 5).
Построение уравнения парной регрессии
При линейной связи параметры уравнения парной регрессии:
 (7.23) находятся из системы уравнений:
(7.23) находятся из системы уравнений:
 , (7.24)
, (7.24)
которая получается применением метода наименьших квадратов. Из первого уравнения системы (7,24) следует, что:
 . (7.25)
. (7.25)
Подставив полученное выражение во второе уравнение, получим:
 . (7.26)
. (7.26)
Коэффициент корреляции определяется по формуле:
 (7.27)
(7.27)
Учитывая (7,26) и (7,27) получим
 (7.28)
(7.28)
или  . (7.29)
. (7.29)
Зная значения r,  и
и 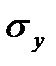 можно вычислить по выражениям (7.29) и (7.25) параметры
можно вычислить по выражениям (7.29) и (7.25) параметры  и
и  линейного уравнения регрессии, а также значение среднего коэффициента эластичности:
линейного уравнения регрессии, а также значение среднего коэффициента эластичности:
 (7.30)
(7.30)
Статистический анализ модели
Оценка параметров парной регрессии выполняется исходя из следующих предпосылок. Допустим, что в генеральной совокупности связь между x и y линейна. Наличие случайных отклонений, вызванных воздействием на переменную y множества других, неучтенных в уравнении факторов и ошибок измерения, приведет к тому, что связь наблюдаемых величин  и
и  приобретает вид:
приобретает вид:
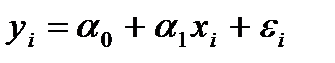 (7.31)
(7.31)
Здесь  - случайные ошибки (отклонения, возмущения). Если были бы известны точные значения отклонений
- случайные ошибки (отклонения, возмущения). Если были бы известны точные значения отклонений  , то можно было бы рассчитать значения параметров
, то можно было бы рассчитать значения параметров  и
и  . Так как они неизвестны, то по наблюдениям
. Так как они неизвестны, то по наблюдениям  и
и  можно получить только оценки параметров
можно получить только оценки параметров  и
и  , которые сами являются случайными величинами в связи с тем, что соответствуют случайной выборке. Пусть
, которые сами являются случайными величинами в связи с тем, что соответствуют случайной выборке. Пусть  - оценка параметра
- оценка параметра  ,
,  - оценка параметра
- оценка параметра  . Тогда оцененное уравнение регрессии будет иметь вид:
. Тогда оцененное уравнение регрессии будет иметь вид:
 (7.32)
(7.32)
Для того чтобы оценки  и
и  обладали адекватностью ряд остатков
обладали адекватностью ряд остатков
 (7.33)
(7.33)
должен удовлетворять следующим требованиям:
1. математическое ожидание  равно нулю (критерий нулевого среднего);
равно нулю (критерий нулевого среднего);
2. величина  является случайной переменной (критерий серий);
является случайной переменной (критерий серий);
3. значения  независимы между собой (критерий Дарбина-Уотсона);
независимы между собой (критерий Дарбина-Уотсона);
4. дисперсия  постоянна:
постоянна: 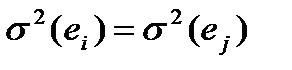 для всех i, j (тест Гольдфельда-Квандта);
для всех i, j (тест Гольдфельда-Квандта);
5. Остатки распределены по нормальному закону (свойство используется для проверки статистической значимости и построения доверительных интервалов при прогнозировании)
Известно, что если данные условия выполняются, то оценки, сделанные с помощью метода наименьших квадратов, обладают следующими свойствами:
- оценки являются несмещенными, т.е. математическое ожидание оценки каждого параметра равно его истинному значению:


Это вытекает из того, что 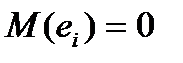 и свидетельствует об отсутствии систематической ошибки в определении положения линии регрессии;
и свидетельствует об отсутствии систематической ошибки в определении положения линии регрессии;
- оценки состоятельны, т.к. дисперсии оценок параметров при возрастании числа наблюдений стремятся к нулю: 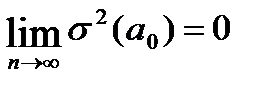 ;
;  т.е. надежность оценки при увеличении выборки растёт;
т.е. надежность оценки при увеличении выборки растёт;
- оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра.
Если предположения 3 и 4 нарушены, т.е. дисперсия возмущений непостоянна или значения  связаны друг с другом, то свойства несмещенности и состоятельности сохраняется, но свойства эффективности – нет.
связаны друг с другом, то свойства несмещенности и состоятельности сохраняется, но свойства эффективности – нет.
Отметим, что аппроксимировать уравнением парной регрессии у на х, имеет смысл только в том случае, если существует достаточно тесная статистическая зависимость между случайными величинами и линейный коэффициент корреляции является значимым, что и имеет место в рассматриваемом примере.
Оценка качества построенной модели
Формально качество модели определяется ее адекватностью и точностью. Эти свойства исследуются на основе анализа ряда остатков (отклонений расчетных значений от фактических):

При этом адекватность является более важной составляющей качества, но сначала рассмотрим характеристики точности и нормальности ряда остатков, так как некоторые из них используются при расчете различных критериев адекватности.
Характеристики точности
Под точностью понимается величина случайных ошибок. Сравнительный анализ точности имеет смысл только для адекватных моделей: среди них лучшей признается модель с меньшими значениями характеристик точности, к которым относятся:
- максимальная ошибка  соответствует максимальному отклонению расчетных значений от фактических;
соответствует максимальному отклонению расчетных значений от фактических;
- средняя абсолютная ошибка 

показывает, насколько в среднем отклоняются фактические значения от модели;
- остаточная дисперсия
 ;
;
- средняя квадратическая ошибка
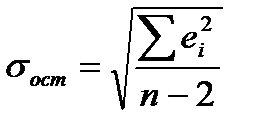 . (7.34)
. (7.34)
Средняя квадратическая ошибка является наиболее часто используемой характеристикой точности (что объясняется ее связью с остаточной дисперсией, которая играет центральную роль в регрессионном анализе). Значение средней квадратической ошибки всегда несколько больше значения средней абсолютной ошибки, но они имеют схожий смысл – характеризуют среднюю удаленность расчетных значений модели от фактических исходных данных. Обычно точность модели признается удовлетворительной если выполняется условие:
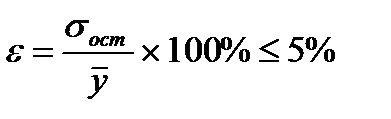 . (7.35)
. (7.35)
К характеристикам точности можно отнести также множественный коэффициент детерминации
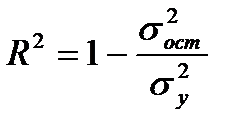 , (7.36)
, (7.36)
характеризующий долю дисперсии зависимой переменной, объясненной с помощью регрессии, и множественный коэффициент корреляции (индекс корреляции):
 . (7.37)
. (7.37)
В случае парной линейной регрессии значение множественного коэффициента корреляции совпадает с линейным коэффициентом корреляции.
Проверка нормальности ряда остатков может быть выполнена приближенно по условиям (7.2). В связи с тем, что каждый из относительных показателей формы распределения меньше 1,5 эмпирическое распределение ряда остатков не противоречит нормальному.
Проверка адекватности модели
Проверка адекватности модели заключается в определении ее значимости и наличии или отсутствии систематической ошибки.
Сначала проверяется значимость параметров уравнения. Если, например, параметр  является незначимым, то необходимо с помощью метода наименьших квадратов получить соответствующее уравнение из которого определяется значение параметра
является незначимым, то необходимо с помощью метода наименьших квадратов получить соответствующее уравнение из которого определяется значение параметра  .
.
Проверка значимости осуществляется на основе t – критерия Стьюдента, т.е. проверяется гипотеза о том, что параметр, измеряющий связь, равен нулю.
Средняя ошибка параметра  равна:
равна:
 , (7.38)
, (7.38)
а для параметра  :
:
 . (7.39)
. (7.39)
Расчетные значения t - критерия вычисляются по формуле:
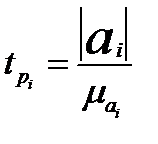 (7.40) Параметр считается значимым, если
(7.40) Параметр считается значимым, если 
Параметр  лежит в пределах
лежит в пределах  ,
,
а параметр  -
-  .
.
Значимость уравнения регрессии в целом определяется с помощью F – критерия Фишера:
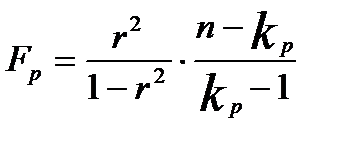 (7.41)
(7.41)
где  - число параметров в уравнении регрессии.
- число параметров в уравнении регрессии.
Расчетное значение F сопоставляется стабличным для числа степеней свободы 
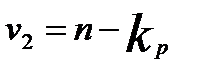 при заданном уровне значимости
при заданном уровне значимости  (например,
(например,  ).
).
Если  , уравнение считается значимым.
, уравнение считается значимым.
Проверка наличия или отсутствия систематической ошибки
1. Проверка свойства нулевого среднего.
Рассчитывается среднее значение ряда остатков  (7.42)
(7.42)
Если оно близко к нулю, то считается, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего, иначе – модель неадекватна по данному критерию. Если средняя ошибка не точно равна нулю, то для определения степени ее близости к нулю используется t – критерий Стьюдента. Расчётное значение критерия вычисляется по формуле
 (7.43)
(7.43)
и сравнивается с критическим  .Если выполняется неравенство
.Если выполняется неравенство  , то модель неадекватна по данному критери
, то модель неадекватна по данному критери