Первый и второй замечательные пределы.
Первый замечательный предел
Определение: Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Применение первого замечательного предела на практике
Пример: Задание. Найти предел 
Решение. Воспользуемся заменой и первым замечательным пределом.
Ответ: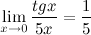 
Следствия из первого замечательного предела
1. 
2. 
3. 
4. 
Второй замечательный предел
Пример: Задание. Найти предел 
Решение. Подставим 
, получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.
Ответ: 
Следствия из второго замечательного предела
1. 
2. 
3. 
4. 
5. 
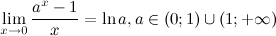
7. 
Задачи,приводящие к понятию производной.
Вводится понятие производной высшего порядка, определяются правила вычисления производных суммы и произведения функций. Даётся определение дифференциала высшего порядка и выводится его связь с производными.
а)о скорости движения материальной точки
б) об угле наклона касательной к графику функции
А.Пусть некоторая материальная точка совершает прямолинейное движение. В момент времени t1 точка находится в положении М1. В момент времени t2 в положении М2. Обозначим промежуток М1,М2 через S; t2-t1= t. Величина S/ t называется средней скоростью движения. Чтобы найти мгновенную скорость точки в положении М1 необходимо t устремить к нулю. Математически это значит, что
Таким образом, для нахождения мгновенной скорости материальной точки необходимо вычислить предел отношения приращения функции S к приращению аргумента t при условии,что t →0
Б. Пусть (t) есть количество вещества прореагировавшего за время t. Спустя 
время количество прореагировавшего вещества будет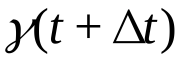 
, т.е. за время 
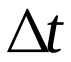количество прореагировавшего вещества 
. Поэтому средняя скорость химической реакции за интервал времени будет равна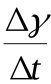 
. Чтобы найти мгновенную скорость химической реакции в момент времени надо устремить к нулю, то естьащению аргумента t при условии,что t →0
Таким образом, производная от количества прореагировавшего вещества определяет мгновенную скорость химической реакции.
Пусть функция 
определена на промежутке X, точка X, дадим ей приращение 
, величина называется приращением аргумента. В каждой из этих точек посчитаем значение функции и. Тогда можно говорить о приращении функции.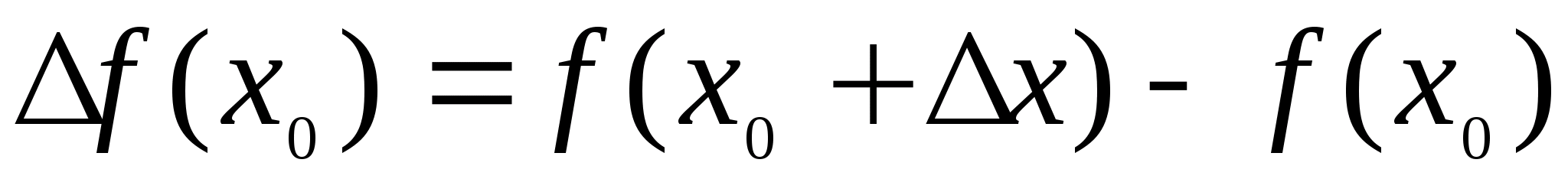 
Определение производной, ее механиеский и геометрический смысл.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Производная. Рассмотрим некоторую функцию y = f (x) в двух точках x0 и x0 +: f (x0) и f (x0 +). Здесь через обозначено некоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f (x0 + х) f (x0) называется приращением функции.Производной функции y = f (x) в точке x0 называется предел: 
Если этот предел существует, то функция f (x) называется дифференцируемой в точке x0. Производная функции f (x) обозначается так: 
Геометрический смысл производной. Рассмотрим график функции y = f (x):
Из рис.1 видно, что для любых двух точек A и B графика функции:
где альфа - угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.В этом и состоит геометрический смысл производной.
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x (t) времени t. В течение интервала времени от t0 до t0 + точка перемещается на расстояние: x (t0 +) x (t0) =, а её средняя скорость равна: va = . При 0 значение средней скорости стремится к определённой величине, которая называетсямгновенной скоростью v (t0) материальной точки в момент времени t0. Но по определению производной мы имеем:
отсюда, v (t0) = x’ (t0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ (t).