Подробный материал представлен в электронной версии
Определение.Два непустых конечных множества называют равночисленными, если между ними можно установить взаимнооднозначное соответствие.
Определение. Взаимнооднозначным (биекцией) между элементами множеств А и В, называют соответствие, обладающее свойствами: каждому элементу множеству А соответствует некоторый элемент множества В; разным элементам множества А соответствуют разные элементы множества В; каждому элементу множества В соответствует некоторый элемент множества А; разным элементам множества В соответствуют разные элементы множества А. Обозначают: А ~ В или А  В.
В.
Определение. Непустые множеств А и В называют равномощными, если существует биекция из множества А на множество В. Обозначают: |A| = |B|.
Определение.Пустые множества А и В равномощны.
Отношение «множество А равномощно множеству В » обладает свойствами рефлексивности, симметричности и транзитивности. Отношение «множество А равномощно множеству В » является отношением эквивалентности, потому можно говорить о разбиении совокупности всех конечных множеств на классы эквивалентных (равночисленных) друг другу множеств. Это разбиение (обозначают М/ ~) обладает следующими свойствами: каждое конечное множество попадает в один класс разбиения; в каждом классе разбиения содержится равночисленные множества (множества, содержащие одинаковое количество элементов).
При таком разбиении множество крыльев орла, множество диагоналей квадрата, множество действительных корней уравнения х2- 4=0, множество общих точек у окружности и секущей попадают в один класс с множеством А={а,в} и т.д.
Пусть А = {*}. Рассмотрим класс всех множеств, эквивалентных множеству А, т.е. множества: {+}, {!}, {— }, {a}, {b}, … Свойство, соответствующее этому классу, обозначим знаком 1.
Добавим к множеству А элемент, не содержащийся в нем, получим новое множество В = {*, o}. Очевидно, что А и В не эквивалентны. Рассмотрим класс всех множеств, эквивалентных множеству В: это множество крыльев орла, множество рук человека, множества диагоналей квадрата и т. д. обозначим общее свойство этого класса знаком 2. Добавим к множеству В элемент, не содержащийся в В, получим новое множество С = В  { ڤ } = {*, o, ڤ }. Общее свойство класса всех множеств, эквивалентных множеству С обозначим знаком 3.
{ ڤ } = {*, o, ڤ }. Общее свойство класса всех множеств, эквивалентных множеству С обозначим знаком 3.
Осуществляя этот процесс получим бесконечную последовательность неэквивалентных друг другу множеств: А, В, С, …, где А 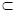 В
В  А
А 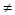 В, В
В, В 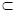 С
С  В
В 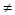 С и т. д. Из принципа построения последовательности очевидно, что
С и т. д. Из принципа построения последовательности очевидно, что
А 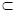 В
В 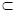 С
С 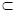 …
…
Рассмотрим последовательность множеств: 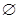 , А = {*}, B = {*, o}, C = {*, o, ڤ }, …
, А = {*}, B = {*, o}, C = {*, o, ڤ }, …
В этой последовательности каждое множество, кроме 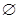 и А получено добавлением к любому конечному множеству элемента, не содержащегося в нем. Отметим, что в этой последовательности (назовем ее цепочкой
и А получено добавлением к любому конечному множеству элемента, не содержащегося в нем. Отметим, что в этой последовательности (назовем ее цепочкой  ) нет множества, на котором прерывается процесс построения множеств; для любых различных множеств X и Y этой последовательности, либо X
) нет множества, на котором прерывается процесс построения множеств; для любых различных множеств X и Y этой последовательности, либо X 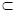 Y, либо Y
Y, либо Y 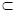 X; в этой последовательности (цепочке
X; в этой последовательности (цепочке  ) нет неравных равномощных множеств.
) нет неравных равномощных множеств.
Определение.Непустое множество называют конечным, если оно равномощно некоторому множеству цепочки  .
.
Определение.Множество называют бесконечным, если в этой последовательности (цепочке  ) нет равномощного ему множества.
) нет равномощного ему множества.
Пример: Множество сторон треугольника конечно, т. к. оно эквивалентно множеству С=В  { ڤ } = {*, o, ڤ }.
{ ڤ } = {*, o, ڤ }.
Определение. Общее свойство класса непустых, эквивалентных друг другу конечных множеств, называют натуральным числом. Если множество А принадлежит классу с общим свойством а, то говорят, что во множестве А содержится а элементов. Обозначают n(А) = а.
Число n(А) = а называют мощностью множества А или количеством элементов множества А.
Множество А называют представителем числа а. Число «нуль» является общим свойством класса, содержащего пустое множество, то есть 0 = n(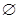 ).
).