Обощенные функции
Дельта-функция Дирака и функция Хэвисайда
Дельта-функцию Дирака вводим на основе преобразования Фурье (см., например, […])
,
.
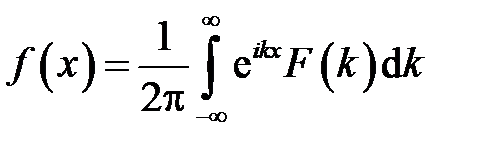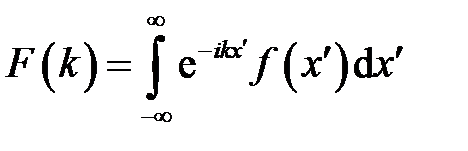Подставив выражение для коэффициента преобразования 
в разложение функции 
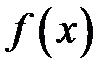, записываем
.
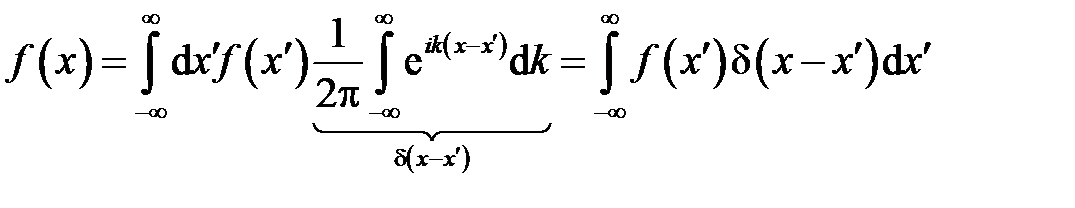В выражении введена обобщенная функция 
, называемая дельта-функцией Дирака. Из выражения следует формула для Фурье преобразования дельта-функции
.
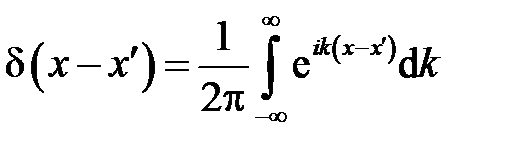Из формул и следуют основные свойства дельта-функции
.
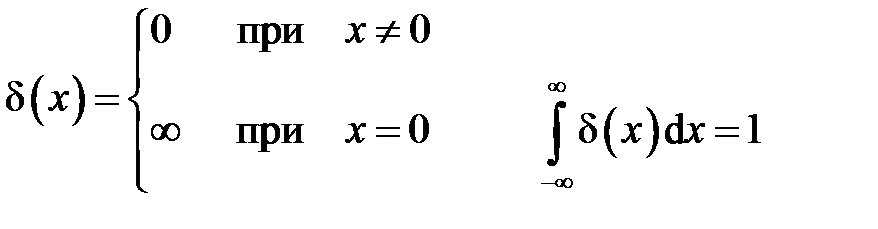Условие нормировки дельта-функции Дирака на единицу вытекает из формулы при условии, что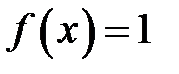 
. Дельта-функция относится к классу обобщенных функций. К подобным математическим объектам средства обычного математического анализа, как правило, неприменимы. Например, производную от дельта-функции 
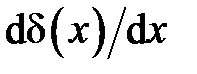невозможно вычислить как предельный переход в математическом анализе. Производную от дельта-функции необходимо определять в интегральном представлении следующим образом
.
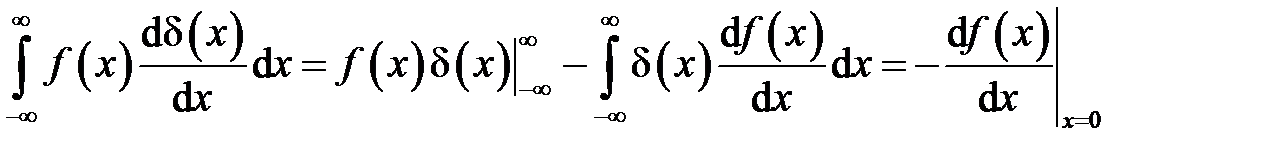При записи используются интегрирование по частям и формула.
Дельта-функция имеет первообразную функцию. Определим функцию скачка, функцию Хэвисайда
.
Из формулы видно, что производная от функции Хэвисайда равна нулю везде, кроме точки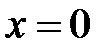 
, где производная обращается в бесконечность. Функция Хэвисайда также является обобщённой. Покажем, что производная от функции скачка Хэвисайда равна дельта-функции Дирака. Рассмотрим выражение
, 
.
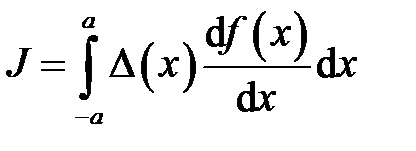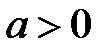С одной стороны, к выражению можно применить процедуру интегрирования по частям
.
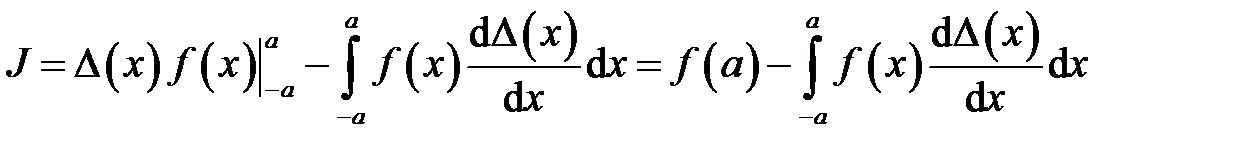С другой стороны, воспользовавшись определением функции Хэвисайда, из формулы получаем
.
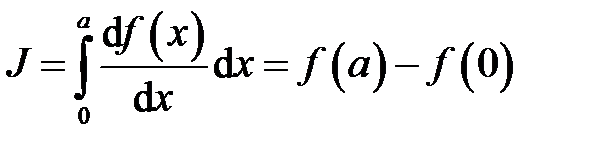Из формул и следует равенство
, 
.
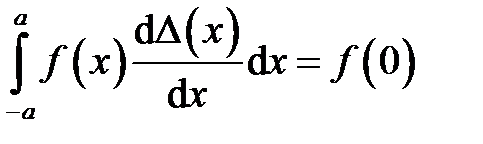Из последнего равенства в переделе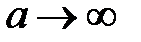 
вытекает
.
Таким образом, формально можно записать связь между обобщенными функциями Дирака и Хэвисайда
.
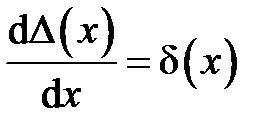Из разложения дельта-функции Дирака в интеграл Фурье получаем разложение в интеграл Фурье функции Хэвисайда
.
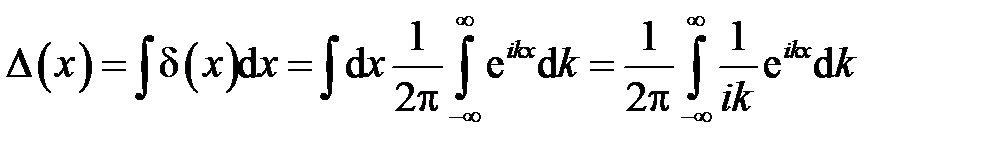Интеграл рассчитываем по теории вычетов (см., например, […]). Контур интегрирования для 
замыкаем в верхней полуплоскости, обходя полюс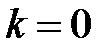 
снизу. По теореме о вычетах, получаем
.
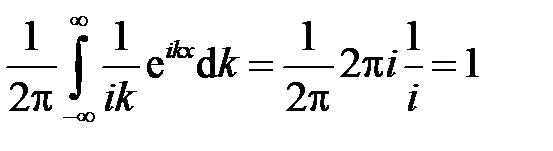Прямой расчет коэффициента разложения функции Хэвисайда в интеграл Фурье приводит к аналогичному результату
.
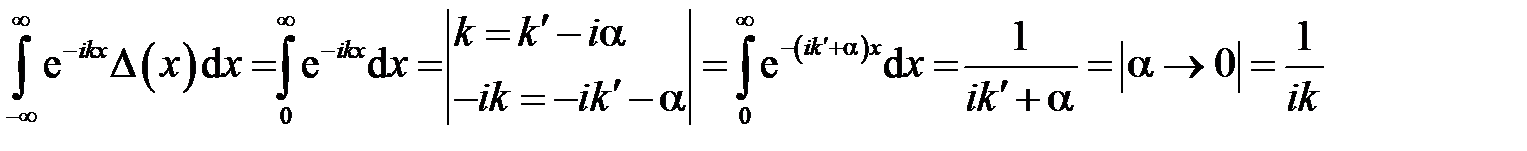Таким образом, обобщенную функцию Хэвисайда можно записать в виде формального разложения
.
Аппроксимации обобщенных функций
У обобщенных функций есть аппроксимации обычными функциями, к которым применимы средства классического математического анализа. Дельта-функцию Дирака можно рассматривать как предел функции Гаусса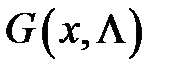 
при стремлении к нулю дисперсии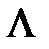 
, 
.
Функция Гаусса нормирована на единицу
.
Перепишем условие нормировки функции Гаусса в следующем виде
.
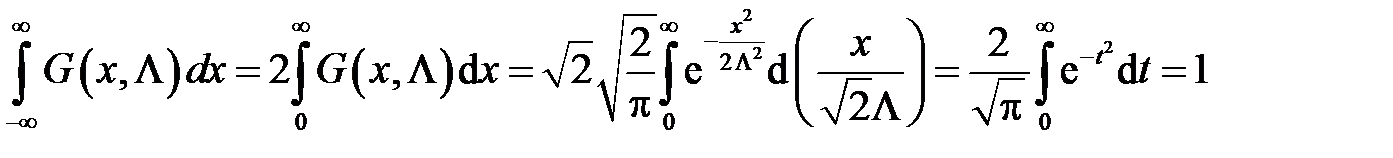Определяем функцию «ошибок»
.
Для функции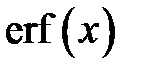 
выполняется предельный переход 
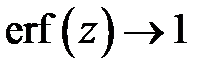, при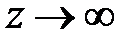 
.
Рис. 1. Аппроксимация функции Гаусса.
На рис. 1 представлен пример поведения функции Гаусса при уменьшении параметра 
.
Аппроксимацию функции Хэвисайда найдем, воспользовавшись тем, что дельта-функция Дирака является производной от функции Хэвисайда. Аппроксимация для функции скачка Хэвисайда получается путем интегрирования аппроксимации функции Гаусса
.
Замена переменных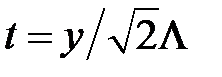 
приводит интеграл к виду
.
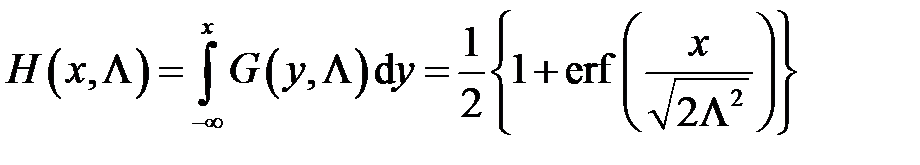При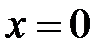 
правая часть этого выражения равна 
, что совпадает со значением функции Хэвисайда в нуле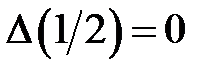 
.
Таким образом, аппроксимацией обобщенной функции Хэвисайда служит выражение
.
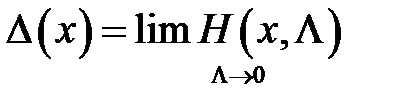Рис. 1. Аппроксимация функции Хэвисайда.
На рис. 2 показана аппроксимация функции Хэвисайда для различных значений параметра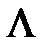 
. Видно, что по мере уменьшения значения параметра 
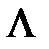аппроксимация стремится у функции скачка 
.