СВОЙСТВА ЖИДКОСТЕЙ. ГИДРОСТАТИКА
1.1. Предмет гидравлики
Гидравлика – прикладная наука, изучающая равновесие, движение и силовое взаимо-действие жидкостей с различными телами.
Предметом гидравлики являются способы приложения законов равновесия и движения жидкостей к решению инженерных задач.
В гидравлике рассматривают в основном потоки жидкости, ограниченные и направлен-ные твердыми стенками, т.е. течение в руслах и каналах.
Гидравлика дает методы расчета гидротехнических сооружений, гидромашин, гид-роприводов и устройств гидропневмоавтоматики.
В гидравлике жидкость представляют однородной непрерывной средой без пустот и проме-жутков, а бесконечно малые частицы жидкости представляют большим числом молекул (не одной молекулой).
Силы, действующие на жидкость. Давление в жидкости.
В гидравлике рассматривают реальную и идеальную жидкости.
Идеальная жидкость не обладает внутренним и внешним трением и является несжимаемой. Это понятие введено как модель для упрощения теоретических выводов и исследований.
Реальная жидкость обладает указанными свойствами.
Силы, действующие на жидкость непрерывно распределены по объему или поверхности жидкости. Они разделяются на массовые и поверхностные.
Массовые силы – это силы тяжести и инерции.
Сила тяжести действует на жидкость постоянно, а силы инерции – при ускоренном ее движении.
Поверхностные силы действуют на границах раздела соседних объемов жидкости, газа или твердых тел.
В соответствии с третьим законом Ньютона, с такими же силами жидкость действует на со-седние объемы или тела.
В гидравлике силы обычно представляют в относительных единицах.
Единичная массовая сила (отнесенная к массе) численно равна ускорению:
Н/кг = [(кг ·м)/с2] / кг = м/с2.
Единичная поверхностная сила (отнесенная к площади) называется напряжением и имеет две составляющие – нормальную и касательную.
Касательное напряжение – это относительная сила трения между слоями жидкости или между жидкостью и твердой стенкой (Н/м2).
Нормальное напряжение – это давление (Н/м2).
Если давление Р отсчитывают от абсолютного нуля, то его называют абсолютным дав-лением Р абс, если от относительного (атмосферного), то – избыточным Р изб (или манометри-ческим).
Атмосферное давление над уровнем моря (рис. 1.1) равно одной физической атмос-фере: Ра = 1 атм = 760 мм. рт ст. = 101325 Па.
Рис. 1.1.
Схема к определению давлений
Кроме физической, используют техническую атмосферу:
Р = 1 атм = 1 кгс/см2 = 98100 Па.
Абсолютное и избыточное давление связаны между собой соотношением:
Р абс = Ра + Р изб.
В Международной системе единиц (СИ) один Паскаль принят за единицу измерения давле-ния: 1 Па = 1 Н/м² = 10-3 кПа = 10-6 мПа.
В инженерном деле за единицу давления принимается одна техническая атмосфера (1 кгс/см2).
1.3. Свойства жидкостей
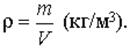
Плотность жидкости – это ее масса, отнесенная к объему:
Удельный вес – это вес жидкости, отнесенный к объему:
Для воды при 4 ºС плотность равна: ρ = 1000 кг/м3.
Удельный вес связан с плотностью: γ = ρg = 1000 кг/м3 · 9,81 м/с2 = 9,81· 103 Н/м3.
Сжимаемость – это свойство жидкости изменять объем под действием давления. Характери-зуется модулем упругости, который представляет собой относительное изменение давления, приходящееся на единицу объема: к = - V (dP / dV) (Н/м2),
где V – первоначальный объем жидкости, dV – изменение этого объема, при увеличении давления на величину dP.
Знак минус указывает на то, что положительному приращению давления, соответствует отрицательное приращение объема.
Для воды к = 2000 МПа, для минерального масла к = 1200 МПа. Если жидкость сжимается, то изменяется и ее плотность.
Сжимаемостью пренебрегают, если давление в жидкости менее 400 кгс/см2.
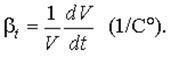Температурное расширение – это относительное изменение объема при увеличении температуры на 1 °С при постоянном давлении. Оно характеризуется коэффициентом температурного расширения:
Для жидкостей коэффициент температурного расширения ничтожно мал и при практических расчетах его не учитывают.
Поверхностное натяжение. Силы поверхностного натяжения возникают на границе раздела жидкости и газа. Они придают объему жидкости сферическую форму и вызывают в ней небольшое давление, определяемое по формуле:
Р = 2σ / r,
где σ – коэффициент поверхностного натяжения жидкости (Н/м), r – радиус сферы.
Например, для воды, при температуре 20 ºС, коэффициент поверхностного натяжения равен 73-3, для спирта – 22,5-3, для ртути – 460-3.
Вязкость жидкости – это свойство сопротивляться сдвигу ее слоев. Вязкость проявляется в возникновении внутренней силы трения между движущимися слоями, определяемой по формуле Ньютона:
где S – площадь слоев жидкости или твердой стенки, соприкасаю-щейся с жидкостью, μ – коэффициент динамической вязкости, dv – приращение скорости, соответствующее приращению координаты dy.
Коэффициент динамической вязкости равен:
где τ - касательное напряжение в жидкости (τ = T/S).
При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обус-ловленное вязкостью.
Скорость течения снижается по мере уменьше-ния расстояния y от стенки вплоть до v = 0 при y = 0, а между слоями происходит проскальзы-вание, сопровождающееся возникновением ка-сательных напряжений τ (силами трения), рис. 1.2.
Рис. 1.2.
Профиль скоростей при течении вязкой жидкос-ти вдоль твердой стенки
Внесистемная единица измерения динамичес-кой вязкости – Пуаз:
1 П = 0,1 Па·с = 0,0102 кгс·с/м2.
Отношение динамического коэффициента вяз-кости к плотности жидкости называется кинематическим коэффициентом вязкости:
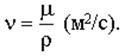
Величина ν, равная 1 см2/с называется стоксом (Ст).
В системе СИ кинематическая вязкость имеет размерность м2/с:
0,01 Ст = 1 сСт = 10-4 м2/с.
Вязкость жидкостей уменьшается при увеличении температуры в соответствии с формулой:
μ = μ 0е – β ΔТ
где μ 0 – динамическая вязкость в начальном состоянии, е – основание натурального лога-рифма (2,718), ΔТ – изменение температуры, β – коэффициент, зависящий от вида жидкости (0,02…0,03), (рис. 1.3).
В инженерном деле чаще пользуются кинематической вязкостью.
Рис. 1.3. Зависимость кинематической вязкости от температуры
Вязкость жидкостей зависит также и от дав-ления, но это существенно при больших давлениях (в несколько десятков МПа):
μ = μ 0е α ΔР ,
где α – коэффициент, зависящий от вида жидкости, ΔР – изменение давления.
Испаряемость жидкости – свойственна всем капельным жидкостям.
Интенсивность испарения зависит от температуры, площади испарения, давления и скорости движения воздуха над свободной поверхностью жидкости.
Чаще мы имеем дело с испарением жидкостей в замкнутых объемах. В этом случае характеристикой испаряемости является давление насыщенных паров Р н.п., выраженное в зависимости от температуры.
Из графиков видно, что с увеличением температуры, давление насыщенных паров возрастает у всех видов жидкости, но немного по-разному.
Рис. 1.4. Зависимость давления насыщенных паров жидкостей от температуры
Рис. 1.5.
Иллюстрация давления насыщенных паров
Давление Р н.п отсчитывается от абсолютного нуля, поэтому, чем оно больше, тем меньше уровень допустимого разряжения в трубопроводе, при котором жидкость будет оставаться однофазной средой.
Если т. А окажется в области разряжения, то в жидкости образуются пустоты (каверны), наполненные ее парами и растворенными газами: образуется двухфазная среда.
Растворимость газов –характеризуется количеством растворенного газа в единице объема жидкости.
При понижении давления (разряжении) растворенный газ выделяется, жидкость разрывает-ся и возникает кавитация. Точка А на рис. 5 поднимается выше.
ГИДРОСТАТИКА
– это раздел гидравлики, рассматривающий законы равновесия жидкости.
2.1. Гидростатическое давление
В неподвижной жидкости возможен только один вид на-пряжения – это напряжение сжатия или гидростати-ческое давление. Если бы возникали касательные нап-ряжения, то происходил бы относительный сдвиг слоев и возникало бы течение.
Рис. 2.1. К выводу основного закона гидростатики
На свободную поверхность жидкости действует давле-ние Р 0.
Определим давление в произвольной точке М, находящейся на глубине h.
Выделим около точки М элементарную горизонтальную площадку, построим на ней вертикальный цилиндр.
Рассмотрим равновесие цилиндра: Р d S – P 0 d S – ρg · h d S = 0,
где Р – давление в точке М, h d S – объем выделенного цилиндра, ρg – удельный вес жидкости (Н/м3), ρg · h d S – вес жидкости в указанном объеме (Н).
Разделим уравнение на d S и решим его относительно Р:
Р = P 0 + ρgh = P 0 + γh
Уравнение называется основным уравнением гидростатики. По нему можно расчитать давление в любой точке неподвижной жидкости.
Показать эпюру давления и центр давления.
Существует еще один закон, называемый законом Паскаля: давление, приложенное к внеш-ней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Математической формулировки этот закон не имеет.
Закон Паскаля лежат в основе работы различных гидростатических машин.
На рис. 2.2 показана схема гид-равлического пресса.
Рис. 2.2.
Принципиальная схема гидравлического пресса
Усилие F 1, действующее на ма-лый поршень площадью S 1, вы-зывает давление в каждой точке жидкости, равное: Р = F 1/ S 1.
В соответствии с законом Паскаля давление Р, передается под большой поршень и воздей-ствует на него с силой, равной:
F 2 = Р · S 2,
которая и воздействует на обрабатываемый объект.
В этом случае внешнее давление в любой точке жидкости намного больше, чем гидростати-ческое давление от веса самой жидкости и им можно пренебречь. Тогда:
Р = F 1 / S 1 = F 2 / S 2.
После преобразования получим силу на большом поршне:
F 2 = F 1 (S 2 / S 1) = F 1 (d 22 / d 21).
Так как диаметр d 2 намного больше диаметра d 1, то мыполучаем значительный выигрыш в силе.
2.2. Давление жидкости на наклонную стенку
Резервуар с наклонной стенкой заполнен жидкостью с удельным весом γ. Ширина стенки равна b, рис. 2.3. Стенка условно развернута относительно оси АВ.
Рис. 2.3. Схема к расчету силы давления на наклонную стенку
Давление изменяется по линей-ному закону:
P = ρgh = γh.
Для построения эпюры давления, найдем Р в точках А и B.
Избыточное давление в точке А будет равно: P A = γh = γ ·0 = 0.
Избыточное давление в точке В:
P B = γh = γH,
где H - глубина резервуара.
Среднее значение давления будет равно: (P A + P B)/2 = (γH)/2.
Площадь стенки S = bL.
Равнодействующая сил давления будет равна: F = [(γH)/2]· S = γ · S · h c,
где h c = Н /2 – глубина погружения центра тяжести наклонной поверхности.
Точка приложения равнодействующей силы давления F проходит через центр тяжести треу-гольника эпюры давления и находится в центре давления ц. д. на расстоянии l цд = 2/3 L, т. е. не совпадает с центром тяжести ц. т. поверхности.
2.4. Прямолинейное равноускоренное движение сосуда с жидкостью
Рассмотрим равновесие жидкости в сосуде при его равноускоренном прямолинейном движении.
Рис. 2.4. Силы, действующие на жидкость при движении цистерны
Кроме силы тяжести действует и сила инерции, вызванная постоянным ускорением а. Возникает новое равновесное состояние, называемое относительным покоем.
Свободная поверхность, где дейст-вует давление Р 0 и все параллель-ные ей –это поверхности уровня, на которых равнодействующая мас-совых сил перпендикулярна к ним.
Равнодействующая относительных массовых сил, рис. 2.4 (т. е. отнесенных к единице массы), определяется векторной суммой:
где – векторы относительных сил инерции и тяжести соответственно.
Давление в любой точке можно определить также, как было найдено давление в неподвижном сосуде.
Выделим около точки М элементарную площадку d S, параллельную свободной поверхности, и построим на ней цилиндр из жидкости, нормальный к ее свободной поверхности.
Условие равновесия выделенного объема будет иметь вид:
Р d S = Р 0 d S + ρ · j · l · d S, (кг/м3)·(м/с2)·м·м2) → кг·м/с2 = Н.
последний член равенства – это полная массовая сила, действующая на выделенный объем, l – расстояние от точки М до свободной поверхности (аналог глубины).
После сокращения на d S получим: Р = Р 0 + ρ · j · l.
В случае, когда а = 0, j = g и формула превращается в основное уравнение гидростатики.