Введение и постановка задачи
Традиционно, вводя определение степенного ряда, полагают, что функцию 
можно представить в форме
.
Далее находят коэффициенты 
. Ясно, что 
, а остальные коэффициенты находятся путем многократного дифференцирования (1):
.
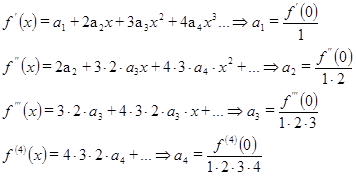Итак:
.
Выражения (1) и (3) описывают разложение функции в ряд Маклорена. Замена переменной x в (1) и (2)на 
дает разложение функции в ряд Тейлора [1] [2]
Все ясно, однако, что если равенство (1) было бы нам не известно? Откуда следует равенство (1)? Приведенный выше ход рассуждений, несмотря на свою простоту, может оставить ощущение непоследовательности у учащихся, которые впервые знакомятся с рядами (обычно начиная именно со степенного ряда). В связи с этим, при изложении учебного материала представляется полезным показать, как прийти к мысли о разложении функции в степенной ряд иначе, как замечая изложенные выше закономерности при дифференцировании многочленов и не привлекая общие теоремы о функциональных рядах.
Степенной ряд, как следствие из определения производной
Из общеизвестного определения производной
,
следует равенство
.
Полагая в выражении (5) 
, 
и упуская символы предела для сокращения записей, найдем приближенное значение функции в точке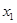 
, зная его в предыдущей точке:
.
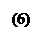
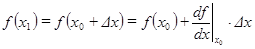Если мы хотим узнать значение функции в следующей точке, то ничего, кроме возрастающей погрешности, не мешает нам произвести действие (6) для точки 
(рис. 1):
.
|
Рисунок 1 - Аппроксимируемая функция ( ).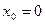
|
Далее, заменяя 
и 
согласно с (6) получаем:
.
Продолжая так для остальных точек, вплоть до точки 
, имеем
, где 
.
Рассмотрим выражение в скобках. Значение производной 
в точке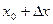 
найдем, воспользовавшись тем же приближением (6):
.
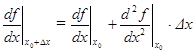Значение производной в следующей точке 
:
.
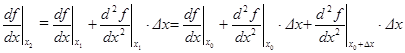Таким же образом для последнего слагаемого получаем выражение аналогичное (8):
.
Учет всех слагаемых в скобках выражения (8) удобно произвести «в столбик»:
Подставляя результат суммирования в (8), запишем
Ясно, что таким же способом можно просуммировать и скобки вновь полученного выражения, то есть:
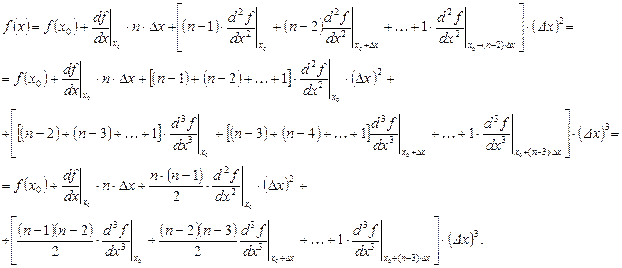
Однако провести суммирование в скобках в этот раз, значительно сложнее и, очевидно, с каждым последующим разом будет все сложнее. В связи с этим вспомним, что мы условились упускать символы предела, то есть, что во всех формулах 
и, следовательно 
(8). Теперь сумму, которая фигурирует в (10), 
, где 
– целое положительное число не больше 
, можно представить как интегральную сумму. Для упрощения изложения положим 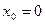(разложение в ряд Маклорена), тогда с учетом (8) имеем:
Обозначим 
переменную, по которой будем производить интегрирование. Она пробегает все значения от 0 до 
с шагом 
, тогда запишем
Теперь повторим преобразования (10) с учетом нашего результата:
Сумму 
, также вводя переменную , перепишем как интегральную сумму:
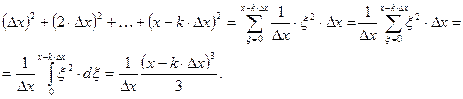
Тогда 
Из выше сказанного нетрудно заключить, что, повторяя изложенные преобразования и отбрасывая последнее слагаемое, как стремящееся к нулю при достаточном количестве суммирований (членов ряда), мы получим разложение функции в ряд Маклорена (1) с коэффициентами (3).
Выводы:
Предполагается, что приведенное изложение способствует более полному пониманию степенных рядов, их связи с базовыми понятиями математического анализа, одновременно являясь поводом для закрепления ранее изученного материала на практике.
Литература
1. Власова Е. А. Ряды. Учеб. для вузов / Е. А. Власова, А. П. Крищенко В. С. Зарубина; МГТУ им. Н.Э. Баумана. – М.:, 2006. – 616 с.
2. Кудрявцев Л. Д. Курс математического анализа. В 3 т. Т.1: Учебник – М.: Дрофа, 2003 – 703 с.