Симметрия уравнений Максвелла и магнитные монополи

Дифференциальная форма уравнений Максвелла

Название	СГС	СИ	Примерное словесное выражение
Закон Гаусса		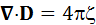	Электрический заряд является источником электрической индукции.
Закон Гаусса для магнитного поля			Не существует магнитных зарядов.
Закон индукции Фарадея			Изменение магнитной индукции порождает вихревое электрическое поле.
Теорема о циркуляции магнитного поля		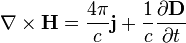	Электрический ток и изменение электрической индукции порождают вихревое магнитное поле

· z – плотность стороннего электрического заряда (в единицах СИ – Кл/м³); в интегральной форме был бы заряд q = zV.

· – плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае (для тока, порождаемого одним типом носителей заряда) выражается как j = u z₁, где — (средняя) скорость движения этих носителей в окрестности данной точки, z₁ — плотность заряда этого типа носителей (она в общем случае не совпадает с z); в общем случае это выражение надо усреднить по разным типам носителей;

· c — скорость света в вакууме (299 792 458 м/с);

· — напряжённость электрического поля (в единицах СИ — В/м);

· — напряжённость магнитного поля (в единицах СИ — А/м);

· — электрическая индукция (в единицах СИ — Кл/м²);

· — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с⁻²•А⁻¹);

Здесь дифференциальный оператор Гамильтона (набла) Ñ = e_x ¶/¶ x + e_y ¶/¶ y + e_z ¶/¶ z, оператор Пуассона ÑÑ = D, при этом:

означает ротор вектора, означает дивергенцию вектора, Ñ .

Приведённые выше уравнения Максвелла ещё не составляют полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины E, B, D, H, j и учитывающие индивидуальные свойства среды, называются материальными уравнениями: D = ε E, B = μ H, E = r j (или j = s E); соответственно ε, μ и r (или s = 1/r) иногда называют материальными параметрами среды.

Симметрия уравнений Максвелла и магнитные монополи

Сформулированные Максвеллом уравнения классической электродинамики связывают электрическое и магнитное поле с движением заряженных частиц. Эти уравнения почти симметричны относительно электричества и магнетизма. Они могут быть сделаны полностью симметричными, если в дополнение к электрическому заряду и току ввести некий магнитный заряд с объемной плотностью распределения z _m и магнитный ток с плотностью j _m:

Название	Без магнитных монополей	С магнитными монополями
Теорема Гаусса:	div D =
Магнитный закон Гаусса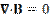
Закон индукции Фарадея:	rot E =
Закон Ампера (с током смещения):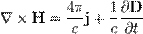

Уравнения из правой колонки переходят в классические уравнения при подстановке и , то есть если в рассматриваемой области пространства отсутствуют магнитные заряды.

Поль Дир а к создал квантовую теорию взаимодействия электрического заряда e с магнитным зарядом g [ q_m ], которая применима при условии:

, где n — целое число. Таким образом, магнитный заряд частицы должен быть кратен элементарному магнитному заряду , где e — элементарный электрический заряд. В используемой системе единиц e и g имеют одинаковую размерность, причём заряд e фиксирован соотношением

[или e ²/ ħc?]

– известная из атомной физики постоянная тонкой структуры.