Анализ динамики социально-экономических явлений
Общая характеристика рядов динамики
Ряды динамики – это статистические данные, характеризующие изменения явлений во времени. В зависимости от характера изучаемого явления различают три вида динамических рядов: моментные, интервальные и ряды средних.
Моментными рядами называются ряды статистических величин, показывающие изменения явления на определенную дату (момент времени). Примером могут служить данные счетов бухгалтерского учета, приведенные на 1-ое число каждого месяца. Данные моментных рядов суммированию не подлежат.
Интервальные ряды – это ряды статистических величин, показывающие изменения явления за определенные временные промежутки (периоды времени). Интервальные ряды можно суммировать. Например, производство продукции предприятием за 1 квартал характеризуется следующими данными: январь – 300 тыс. грн., февраль – 305 тыс. грн., март – 306 тыс. грн.
Ряды, характеризующие изменения средних уровней изучаемого явления во времени, называются рядами средних величин.
Динамические ряды характеризуются при помощи показателей, определяющих характер, интенсивность, направление.
Показатели динамики рядов
Средний уровень ряда определяется в зависимости от вида динамического ряда. Если ряд моментный с равными промежутками между датами, то используют формулу средней хронологической.
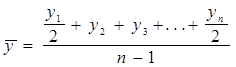, где
| y1, y2,...,yn | – фактические значения уровней моментного ряда, |
| n | – число уровней. |
Средний уровень интервального ряда с равными промежутками между датами определяют по средней арифметической простой:
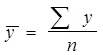, где
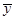
| – средний уровень, |
| y | – фактические значения уровней ряда, |
| n | – число уровней. |
Если промежутки между датами не равные, то средний уровень ряда вычисляют по средней арифметической взвешенной.
Цепные показатели получают, если каждый уровень последующий сравнивают с предыдущим.
Базисные показатели получают, если каждый уровень последующий сравнивают с первоначальным уровнем, принятый за базу сравнения.
Показатель, показывающий скорость роста – абсолютный прирост. Он определяется как разность между двумя сравниваемыми уровнями и показывает на сколько один уровень больше (меньше) по сравнению со сравниваемым уровнем.
– цепной, где
| – абсолютный прирост, |
| yi | – текущий уровень, |
| yi-1 | – предшествующий уровень ряда. |
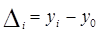– базисный,
где y0 – начальный уровень ряда.
Средний абсолютный прирост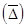 
рассчитывается по формуле:
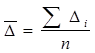, где
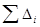
| – сумма цепных приростов, |
| n | – число приростов. |
Средний абсолютный прирост показывает на сколько в среднем увеличивается (уменьшается) изучаемое явление.
Коэффициент роста (КР) – определяется как отношение двух сравниваемых уровней и показывает, во сколько раз один уровень больше (меньше) по отношению со сравниваемым.
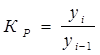– цепной, 
– базисный.
Если коэффициенты роста выражают в процентах, то они называются темпами роста (ТР):
.
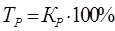Темп прироста показывает на сколько процентов увеличился (уменьшился) текущий уровень по сравнению с базисным, принятым за 100%.
Темп прироста можно рассчитать по данным о темпе роста. Для этого надо от темпа роста вычесть 100 или от коэффициента роста – единицу, тогда получим коэффициент прироста.
ТПР=ТР-100%.
Среднегодовой коэффициент роста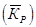 
определяется по средней геометрической:
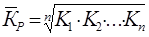, где
| K1K2...Kn | – произведение цепных коэффициентов роста, |
| n | – число коэффициентов роста. |
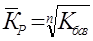, где
| Кбаз | – базисный коэффициент роста за весь период, |
| n | – число лет. |
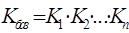или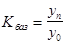 
, где yn и y0 – конечный и первоначальный уровни ряда.
Средний коэффициент роста показывает, во сколько раз в среднем за рассмотренный период изменились уровни динамического ряда.
Средний темп роста 
определяется по следующей формуле: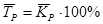 
.