1. ИСХОДНЫЕ ДАННЫЕ
Таблица А1
Исходные данные
| Переменная | Координаты | ||||
| первая | вторая | третья | четвертая | пятая | |
| |||||
| ? |
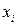
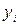
2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ
Для начала необходимо определить суммы значений 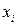и 
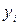(при этом пятую координату пока не учитываем), которые определяются как:
; 
.
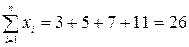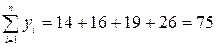Далее определим суммы значений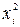 
и произведений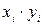 
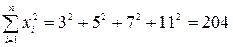
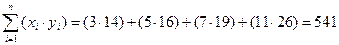
Вычислим коэффициенты линейной регрессии по формулам (3) и (4):
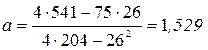
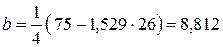
Составим искомое уравнение линейной регрессии вида (1):
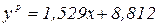
3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ДЕТЕРМИНАЦИИ
Перед тем как определить коэффициент детерминации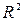 
произведем расчет 
.
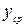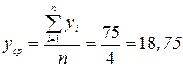
Далее определим значения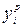 
; объясненную вариацию 
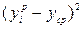и общую вариацию 
для первой координаты:
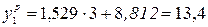
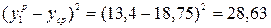
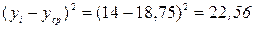
Аналогично произведем расчет и для остальных координат, результаты расчетов сведем в таблицу А2
Таблица А2
Результаты расчетов объясненной и общей вариаций
| Координата | Параметры | ||||
| 
|
| 
| 
| |
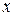
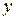
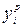
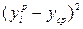
| Первая | 13,4 | 28,63 | 22,56 | ||
| Вторая | 16,46 | 5,26 | 7,56 | ||
| Третья | 19,52 | 0,56 | 0,06 | ||
| Четвертая | 25,63 | 47,35 | 52,56 |
Вычислим коэффициент детерминации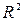 
по выражению (5):
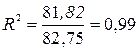или 99%
4. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ В ПРОГРАММЕ MS EXCEL
Проведем регрессионный анализ с использованием режима «Регрессия» в программе MS Excel. Подготовка расчета представлена на рисунке А1, а результаты расчетов в таблицах А3-А5.
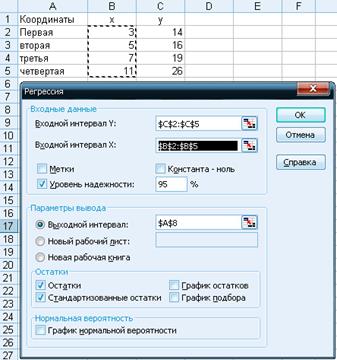
Рис. А1. Подготовка расчета в программе MS Excel
Таблица А3
Регрессионная статистика
| Множественный R | R-квадрат | Нормированный R-квадрат | Стандартная ошибка | Наблюдения |
| 0,99 | 0,98 | 0,98 | 0,7 | 4,000 |
Таблица А4
Параметры регрессии
| Параметры | Коэффициенты | Стандартная ошибка | t-статистика |
| Y-пересечение | 8,814286 | 0,841282 | 10,47721 |
| Переменная X 1 | 1,528571 | 0,117803 | 12,97566 |
Таблица А5
Вывод остатка
| Наблюдения | Предсказанное Y | Остатки | Стандартные остатки |
| 13,4 | 0,6 | 1,054402535 | |
| 16,45714286 | -0,457142857 | -0,803354312 | |
| 19,51428571 | -0,514285714 | -0,903773601 | |
| 25,62857143 | 0,371428571 | 0,652725379 |
Значения таблицы А4 показывают, что это уравнение, совпадает с уравнением, полученным при расчете по МНК вручную с точностью до ошибки округления.
В данном расчете коэффициент регрессии оказался положительным, следовательно, связь также является положительной.
Данные таблицы А5 показывают величину отклонения каждой точки от построенной линии регрессии. Наибольшее абсолютное значение остатка – 0,6, наименьшее - 0,37. Для наглядности построим график линейной регрессии, представленный на рисунке А2.
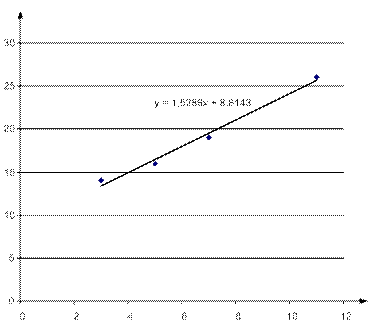
Рис. А1. График линейной регрессии для данного числового ряда
Поскольку коэффициент детерминации имеет достаточно высокое значение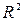 
>100% следовательно, полученное уравнение линейной регрессии, возможно использовать для прогнозирования.
Определим параметр 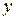для пятой координаты:
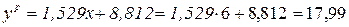
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ………………………………………………………………….. | |
| Общие методические указания по выполнению контрольной работы | |
| КОНТРОЛЬНАЯ РАБОТАСоздание уравнения регрессионной модели и проверка его адекватности…………………………………….. | |
| РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА………………………………………… | |
| ПРИЛОДЕНИЕ А……………………………………………………………… |