Построение векторных диаграмм токов и напряжений

Липецкий государственный технический университет

Кафедра Электрооборудования

 

 

ЛАБОРАТОРНАЯ РАБОТА №1

по ТОЭ

Исследование цепи простейших цепей переменного тока и явления резонанса

 

Студент ______________ Фролов С.Н

Группы ЭО-14-2

 

Руководитель Довженко С. В.

 

Липецк 2015 г.

Определение параметров элементов электрической цепи

 

В таблице 1 приведены показания приборов и результаты, полученные в результате вычислений в опыте №1. Исходные данные: Uвх=17В

Таблица 1. Результаты измерений

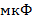
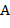
	0,32		17,7
				11,4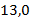
					34,8
		12,5

Таблица 2. Результаты расчетов

53,078	35,49	14,77	34,06	38,44	53,12	0,92	4,73	11,36
39,809	36,61	15,36	35,15	39,69	51,52	0,98	5,07	12,1
26,539	35,57	14,05	33,53	38,24		0,95	4,78	12,1
45,496	35,76	11,68		37,62	18,38	0,64	10,8	33,08
35,386	35,52	11,67		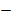36,39	13,88	0,84	14,3	43,5
31,847	34,87	12,0		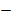36,88	13,6	0,88		43,6
28,952	35,46	11,77		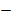37,36	14,47	0,81	13,83	41,67

Окончание таблицы 2.

24,498

35,46

12,5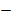

37,6

0,74

12,5

35,46

Расчетные формулы:

(1)

где – реактивное сопротивление конденсатора, Ом,

– частота переменного тока, Гц,

– емкость конденсатора, мкФ.

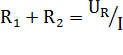(2)

где – первый и второй резисторы соответственно, Ом,

– напряжение на зажимах резистора, В,

– сила тока в цепи, А.

(3)

где – активное сопротивление катушки индуктивности, Ом,

– активная мощность, Вт,

– полное сопротивление катушки индкутивности, Ом,

- коэффициент мощьности.

(4)

где – полное сопротивление катушки индкутивности, Ом,

– напряжение на зажимах катушки индуктивности, В.

(5)

где – реактивное сопротивление катушки индуктивности, Ом. (6)

где – полное сопротивление, Ом,

– напряжение в цепи, В,

– сила тока в цепи, А.

(7)

где - коэффициент мощности.

(8)

где – величина вектора напряжения для резистора, В.

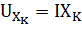(9)

где – величина вектора напряжения для катушки индуктивности, В.

Используя формулу (1) найдем реактивное сопротивление для каждого конденсатора:

=53,078 Ом

=39,809 Ом

=26,539 Ом

=45,496 Ом

=35,386 Ом

=31,847 Ом

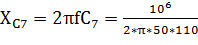=28,952 Ом

=24,498 Ом

 

 

По формуле (4) найдем полное сопротивление катушки индкутивности:

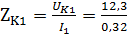=38,44 Ом

=39,69 Ом

=38,24 Ом

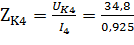=37,62 Ом

=37,39 Ом

=36,88 Ом

=37,36 Ом

=37,60 Ом

 

По формуле (7) вычислим коэффициент мощности:

=0,92

=0,98

=0,95

=0,64

=0,84

=0,88

=0,81

=0,74

 

Используя полученные значения по формулам (4) и (7), найдем с помощью формулы (3) активные сопротивления катушек индуктивности

=15,36 Ом

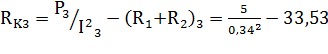=14,05 Ом

=11,68 Ом

=11,67 Ом

=12,0 Ом

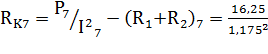=11,77 Ом

=12,50 Ом

Зная полное сопротивление катушки индкутивности и активное сопротивление катушки индуктивности , по формуле (5) найдем реактивные сопротивления катушек индуктивности:

=35,49 Ом

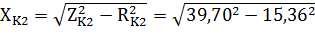=36,61 Ом

=35,57 Ом

=35,76 Ом

=35,52 Ом

=34,87 Ом

=35,46 Ом

=35,46 Ом

Полное сопротивление равно:

=53,12 Ом

=51,52 Ом

=50,0 Ом

=18,38 Ом

=13,88 Ом

=13,60 Ом

=14,47 Ом

=17,0 Ом

По формулам (8) и (9) найдем величина вектора напряжения для резистораи катушки индуктивности соответственно

=4,73 В

=5,07 В

=4,78 В

=10,8 В

=14,3 В

=15,0 В

=13,83 В

=12,5 В

 

=11,36 В

=12,1 В

=12,1 В

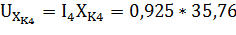=33,08 В

=43,5 В

=43,6 В

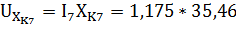=41,67 В

=35,46 В

 

 

Построение векторных диаграмм токов и напряжений

 

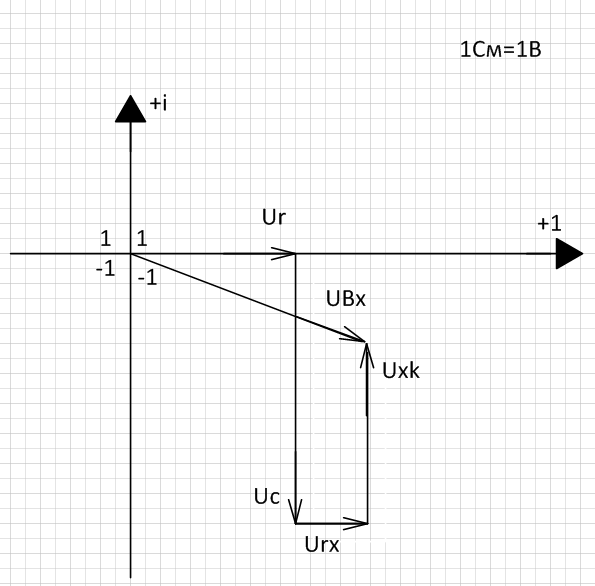
Рисунок 1 Векторная диаграмма напряжения для С=60мкФ

 

Рисунок 2 Векторная диаграмма напряжения для С=80мкФ

 

Рисунок 3 Векторная диаграмма напряжения для С=120мкФ

 

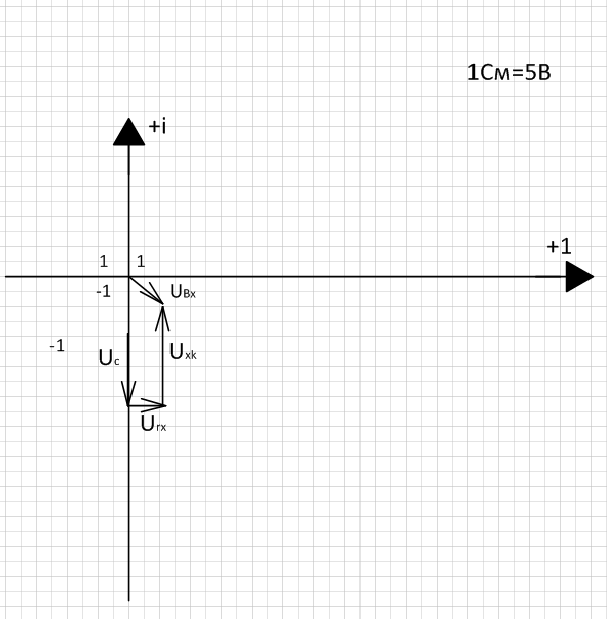
Рисунок 4 Векторная диаграмма напряжения для С=70мкФ

 

 

Рисунок 5 Векторная диаграмма напряжения для С=90мкФ

 

 

Рисунок 6 Векторная диаграмма напряжения для С=100мкФ

 

 

Рисунок 7 Векторная диаграмма напряжения для С=110мкФ

 

 

Рисунок 8 Векторная диаграмма напряжения для С=130мкФ

 

 

Таблица 3. Результаты измерений

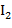
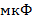
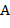
	2,5
	2,5
			0,4
				0,41

Таблица 4. Результаты расчетов

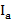
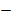
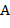
0,013		0,0065	0,0038	0,015	0,011	0,668	0,1514	0,160
0,009		0,009	0,022			0,919	0,14704	0,063
0,009		0,009	0,022			0,919	0,14704	0,063
0,01		0,008	0,022			0,865	0,14705	0,085
0,014		0,0075	0,022			0,767	0,17641	0,148

 

Расчетные формулы:

(1)

где – модуль проводимости катушки индуктивности, См

- ток в ветви с катушкой индуктивности и резистором, А

U - напряжение в цепи, В.

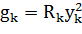(2)

где – активная составляющая катушки индуктивности, См

(3)

где – реактивная составляющая катушки индуктивности, См

(4)

где – реактивная составляющая конденсатора, См,

- реактивное сопротивление конденсатора, Ом

(5)

где 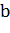– полная реактивная составляющая всей цепи, См

(6)

где 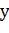– модуль полной проводимости цепи, См

(7)

где - коэффициент мощности.

(8)

(9)

Используя формулу (1) найдем модуль проводимости катушки индуктивности:

См.

По формуле (2) вычислим активную составляющую катушки индуктивности:

 

Используя полученные значения по формулам (1) и (2), найдем реактивную составляющую катушки индуктивности по формуле (3):

См.

См.

См.

См.

См.

Рассчитаем по формуле (4) реактивную составляющую конденсатора:

=0,015 См

=0,022 См

=0,025 См

=0,028 См

=0,031 См

 

 

Используя полученные значения,найденные по формулам (3) и (4), вычислим полную реактивную составляющую всей цепи по формуле (5):

=0,0112 См

=0 См

=0,003 См

=0,006 См

=0,009 См

 

По формуле (6) найдем модуль полной проводимости цепи:

=0,013 См

=0,009 См

=0,009 См

=0,01 См

=0,014 См

Используя формулу (7), найдем коэффициент мощности в данной цепи:

=0,668

=0,919

=0,919

=0,865

=0,767

Найдем значения

и :

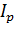=0,1514 А =0,160 А

=0,14704 А =0,063 А

=0,14704 А =0,063 А

=0,14705 А =0,085 А

=0,17641 А =0,148 А

 

 

 

Рисунок 9 Треугольник проводимости до резонанса токов (С = 50 мкФ)

 

Рисунок 10 Треугольник проводимости до резонанса токов (С = 70 мкФ)

 

Рисунок 11 Треугольник проводимости до резонанса токов (С = 80 мкФ)

 

Рисунок 12 Треугольник проводимости до резонанса токов (С = 90 мкФ)

 

 

Рисунок 13 Треугольник проводимости до резонанса токов (С = 100 мкФ)

 

 

Рисунок 14 Векторная диаграмма токов и напряжений для (С=74 мкФ)

 

Рисунок 15 Векторная диаграмма токов и напряжений для (С=64 мкФ)

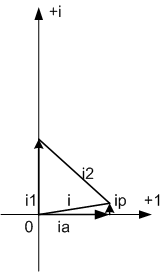
Рисунок 16 Векторная диаграмма токов и напряжений для (С=44 мкФ)