Комплексные числа
Рассмотрим следующие вопросы:
1) Понятие комплексного числа.
2) Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел.
3) Тригонометрическая и показательная форма комплексного числа.
4) Возведение комплексных чисел в степень.
5) Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Вспомним множество действительных чисел, обозначаются буквой 
(в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа находятся на числовой прямой:
Здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.
Понятие комплексного числа
Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве.
Если хотите, комплексное число – это двумерное число. Оно имеет вид 
, где 
и 
– действительные числа,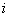 
– так называемая мнимая единица. Число называется действительной частью (
) комплексного числа 
, число называется мнимой частью(
) комплексного числа .
– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: 
или переставить мнимую единицу: 
– от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:
Геометрическая интерпретация. Комплексные числа изображаются на комплексной плоскости:
Как упоминалось выше, буквой принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой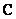 
. Поэтому на чертеже следует поставить букву 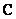, обозначая тот факт, что у нас комплексная плоскость.
Комплексная плоскость состоит из двух осей:
– действительная ось
– мнимая ось
Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат. По осям нужно задать масштаб, отмечаем:
ноль;
единицу по действительной оси;
мнимую единицу 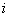по мнимой оси.
Построим на комплексной плоскости следующие комплексные числа:
, 
, 
, 
, 
, 
, 
, 
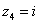Рассмотрим следующие комплексные числа: , , . Действительные числа – это частный случай комплексных чисел. Действительная ось обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел является подмножеством множества комплексных чисел .
Числа , , – это комплексные числа с нулевой мнимой частью.
Числа 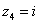, , – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .
В числах , , , и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому что они сливаются с осями.
Алгебраическая форма комплексного числа.
Сложение, вычитание, умножение и деление комплексных чисел
– это алгебраическая форма комплексного числа. Существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.
Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.