3.1. Опорные системы координат.
Формы и размеры Земли могут быть описаны двумя способами. Один способ - описание видимой физической поверхности, включая поверхности морей и океанов, равнины, склоны холмов и горы. Второй способ - это измерение силы тяжести. Эти два подхода объединяются, когда мы говорим, что высота Эвереста составляет 8848 метров над средним уровнем моря.
Геоид - это уровненная поверхность потенциала силы тяжести, совпадающая с точностью около 1 метра с уровнем Мирового океана в спокойном состоянии. Вертикальное положение объекта на земной поверхности можно определить, измерив значение силы тяжести в данной точке и сравнив его со значением силы тяжести на среднем уровне моря. К сожалению, геоид - это сложная поверхность, которая не может быть точно описана замкнутой математической формулой.
Рис 3.1.1. Геоид.
Математические модели могут быть близки к описываемой поверхности, но не являются её копиями. Если Земля была бы полностью жидкой, то при вращении она имела бы форму эллипсоида. Поэтому эллипсоид является хорошим математическим приближением к естественной форме геоида (см. рис. 3.1.1.).
Движение НИСЗ происходит по законам небесной механики под действием инерции и гравитационных полей небесных тел и различных возмущающих факторов (солнечный ветер, магнитные поля и другие). Для описания такого движения используется геоцентрическая система координат OXYZ, связанная с Землёй. Геоцентрическая система координат СРНС ГЛОНАСС - параметры Земли 1990 года - ПЗ-90, а СРНС GPS - всемирная геодезическая система 1984 года - WGS-84. Передаваемые каждым НИСЗ системы ГЛОНАСС в составе оперативной информации эфемериды описывают положение фазового центра передающей антенны данного НИСЗ в геоцентрической системе координат ПЗ-90, определяемой следующим образом:
|
|
НАЧАЛО КООРДИНАТ расположено в центре масс Земли;
ОСЬ Z направлена на Условный полюс Земли, как определено в рекомендации Международной службы вращения Земли (IERS);
ОСЬ X направлена в точку пересечения плоскости экватора и нулевого меридиана, определенного Международным бюро времени (BIH);
ОСЬ Y дополняет геоцентрическую прямоугольную систему координат до правой.
Интервал времени между двумя такими последовательными моментами соответствует одним звездным суткам.
Рис. 3.1.2. Геоцентрическая подвижная система координат.
В геоцентрической подвижной системе координат формируется информация о движении спутников, которая передается в навигационном сообщении потребителю. В этой же системе координат на этапе вторичной обработки информации в аппаратуре потребителя рассчитываются координаты самого потребителя.
Однако потребителя в большей степени интересуют такие координаты, как высота, широта и долгота, которые относятся к геодезической системе координат. Геодезические координаты точки связаны с математической моделью Земли в виде эллипсоида (рис. 3.1.3.) с большой полуосью а, лежащей в экваториальной плоскости, и малой полуосью b. Геодезическая широта В точки П определяется как угол между нормалью к поверхности эллипсоида и плоскостью экватора. Геодезическая долгота L точки П определяется как угол между плоскостью начального меридиана и плоскостью меридиана, проходящего через точку П (положительное направление счета долгот – от Гринвичского меридиана к востоку). Геодезическая высота Н определяется как расстояние по нормали от поверхности эллипсоида до точки П.
|
|
Найденные в ходе навигационных определений прямоугольные геоцентрические координаты { x, y, z } потребителя должны быть преобразованы в геодезические координаты { B, L, H }.
Рис. 3.1.3. Земной эллипсоид.
Указанные координаты связаны соотношениями:
х = (N + H) ∙ cosB ∙ cоsL;
у = (N + B) ∙ cosB ∙ sinL;
z = [(l -e2)∙N + H] ∙ sinВ.
где N = 
- эксцентриситет эллипсоида;
α = 1 - Ь/ α - параметр сжатия эллипсоида;
е =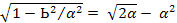 
- эксцентриситет эллипсоида.
Для определения координат потребителя необходимо знать координаты спутников (не менее 4) и дальность от потребителя до каждого видимого спутника. Для того чтобы потребитель мог определить координаты спутников, излучаемые ими навигационные сигналы моделируются сообщениями о параметрах их движения. В аппаратуре потребителя происходит выделение этих сообщений и определение координат спутников на нужный момент времени.
Координаты и составляющие вектора скорости меняются очень быстро, поэтому сообщения о параметрах движения спутников содержат сведения не об их координатах и составляющих вектора скорости, а информацию о параметрах некоторой модели, аппроксимирующей траекторию движения КА на достаточно большом интервале времени (около 30 минут). Параметры аппроксимирующей модели меняются достаточно медленно, и их можно считать постоянными на интервале аппроксимации.
Параметры аппроксимирующей модели входят в состав навигационных сообщений спутников. В системе GPS используется Кеплеровская модель движения с оскулирующими элементами. В этом случае траектория полёта КА разбивается на участки аппроксимации длительностью в один час. В центре каждого участка задается узловой момент времени, значение которого сообщается потребителю навигационной информации. Помимо этого, потребителю сообщают параметры модели оскулирующих элементов на узловой момент времени, а также параметры функций, аппроксимирующих изменения параметров модели оскулирующих элементов во времени как предшествующем узловому элементу, так и следующем за ним.
|
|
В аппаратуре потребителя выделяется интервал времени между моментом времени, на который нужно определить положение спутника, и узловым моментом. Затем с помощью аппроксимирующих функций и их параметров, выделенных из навигационного сообщения, вычисляются значения параметров модели оскулирующих элементов на нужный момент времени. На последнем этапе с помощью обычных формул Кеплеровской модели определяют координаты и составляющие вектора скорости спутника.
Широкое использование в приёмоиндикаторах GPS алгоритмов оптимальной фильтрации, а также новых технологий, что позволит существенно повысить их эффективность и улучшить тактико-технические характеристики, а также позволит решать принципиально новые задачи. Например, такие, как определение пространственной ориентации летательного аппарата, автоматический заход на посадку до касания, автоматизированную дозаправку топливом в полете, полеты в плотных боевых порядках и др.
3.2. Системы местоопределения, использующие специализированную спутниковую радионавигационную систему.
Как было сказано выше, для определения координат потребителя необходимо знать координаты спутников (не менее 4) и дальность от потребителя до каждого видимого спутника, которая определяется в навигационном приёмнике с точностью 1 м.
Рис. 3.2.4. Определение координат пользователя.
Каждый спутник можно представить в виде точечного излучателя. В этом случае фронт электромагнитной волны будет сферическим. Точкой пересечения двух сфер будет та, в которой находится потребитель.
Высота орбит спутников составляет порядок 20000 км. Следовательно, вторую точку пересечения окружностей можно отбросить из-за априорных сведений, так как она находится далеко в космосе.
Схема построения системы местоопределения с двумя геостационарными спутниками связи представлена на рис. 3.2.5. Примером таких систем могут служить системы EUTELTRACS (ЕСА) и GEOSTAR (США).
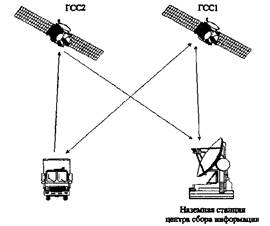
Рис. 3.2.5. Система местоопределения, использующая геостационарные спутники связи.
Спутники ГСС-1 и ГСС-2 не являются составной частью системы местоопределения, они выполняют роль ретрансляторов сигналов в линии радиосвязи между наземной станцией центра сбора и аппаратурой подвижного объекта.При этом ГСС-1 обеспечивает ретрансляцию сигналов от наземной станции к подвижному объекту и обратно, а ГСС-2 только от подвижного объекта к наземной станции.
Координаты подвижного объекта вычисляются на наземной станции по сигналам, полученным от подвижного объекта с двух направлений (от ГСС-1 и ГСС-2) система четырех объектов, в которой координаты трех объектов ГСС-1, ГСС-2 и наземной станции известны, позволяет по методу триангуляции рассчитать координаты четвертого объекта, если измерить дальности от подвижного объекта до ГСС-1 и ГСС-2. Приближенно это можно представить следующим образом. Если измерены дальности от ГСС-1 и ГСС-2 до объекта L1 и L2, то подвижный объект находится на линии пересечения двух сфер, описанных радиусом L1 с центром на ГСС-1 и радиусом L2 с центром на ГСС-2. Пересечение же этой линии с поверхностью Земли даст точку местоположения подвижного объекта.
В настоящее время разрабатываются и в ближайшие годы будут вводиться в эксплуатацию глобальные системы спутниковой связи, базирующиеся на группировке низкоорбитальных (высота около 1000 км) спутников. Принцип организации связи предполагает, что в зоне видимости объекта связи в каждый момент времени находится не менее 2-х спутников. Управление связью осуществляется через сеть базовых наземных станций, которые, обеспечивая условия вхождения объекта в связь через спутник, решают задачи синхронизации аппаратуры подвижного объекта по времени, фазе и частоте излучаемых ею сигналов. При этом информация, которой располагает наземная станция при решении задачи установления связи, содержит необходимый объем данных для определения координат объекта связи как побочный продукт для предоставления услуг по местоопределению объекта, будь он подвижный или неподвижный.
3.3. Краткий обзор существующих методов определения координат потребителя посредством СРНС ГЛОНАСС/GPS.
В зависимости от типа решаемой задачи, требований к точности определения координат, аппаратуры потребителя, а также применяемых математических алгоритмов и программного обеспечения на настоящий момент, существуют различные методы определения координат посредством СРНС ГЛОНАСС/Navstar GPS. Рассмотрим их.
Абсолютный метод.
По известным координатам минимум 4 НИСЗ и измеренным до них расстояниям потребитель вычисляет свои координаты (t, X, Y и Z) относительно центра эллипсоида ПЗ-90 или WGS-84 с точностью порядка 18 м в плане и 28 м по высоте (в 95% случаев по всему миру в любое время суток и независимо от метеоусловий).
Метод дифференциальной коррекции.
Метод дифференциальной коррекции предполагает наличия как минимум двух навигационно-геодезических приёмников (НГП) в двух точках пространства на удалении до 200 км. При реализации метода дифференциальной коррекции координаты потребителя и опорного НГП получают абсолютным методом. По измеренным псевдодальностям по коду до НИСЗ для одного и того же момента излучения радионавигационного сигнала потребитель определяет задержку получения радионавигационного сигнала относительно опорного НГП. Зная время распространения электромагнитного сигнала от НИСЗ между двумя приёмниками с ошибкой не более 10–7 с, потребитель определяет приращение координат между собственным и опорным НГП с ошибкой не более 1 м. В основе метода дифференциальной коррекции лежит относительное постоянство значительной части ошибок передаваемого сигнала от НИСЗ «Ураган» или «Navstar» во времени и пространстве за ионосферу, тропосферу и эфемеридную информацию, в случае близкого расположения двух и более НГП относительно друг друга. Так как сигналы от НИСЗ «Ураган» или «Navstar», которые удалены от потребителя на расстояние более 19 000 километров, достигают этих НГП по очень близким траекториям.
Метод дифференциальной коррекции подразделяется на:
– Дифференциальный режим с коррекцией координат. Его принцип основан на вычислении ошибки полученных мгновенных координат опорного НГП в общеземной системе координат относительно точных координат опорного навигационно-геодезического приёмника в общеземной системе координат. С учётом ошибки определения мгновенного местоположения опорного НГП вносится коррекция либо в координаты потребителя, либо в измеренные НГП потребителя псевдодальности.
– Дифференциальный режим с использованием относительных координат. Используется в случае затруднения в точной геодезической привязке опорного НГП. В качестве точных координат используются мгновенные координаты, осреднённые за определённый период времени.
– Дифференциальный режим с использованием псевдоспутника. В местах, где невозможно наблюдение потребителем более 3-х работоспособных НИСЗ синхронно с опорным НГП, устанавливают устройство, имитирующее сигнал НИСЗ. Данное устройство называют псевдоспутником. Дифференциальный режим определения местоположения по НИСЗ и псевдоспутнику назван дифференциальным режимом с использованием псевдоспутника.
– Относительные фазовые определения. Данный режим наиболее сложен в математической реализации. Точность и дальность действия в плане для неподвижного потребителя, при реализации метода относительных фазовых определений, составляет 3 мм + ошибка в 1 мм на каждый километр. Метод основан на оценке фазовой задержки радионавигационного сигнала во времени от одного и того же НИСЗ относительно нескольких НГП с учётом их пространственного положения.
Для реализации режима в качестве исходных данных используют, помимо измеренных псевдодальностей по кодовой последовательности до НИСЗ, измеренную дробную часть поступающей фазы радионавигационного сигнала с ошибкой не более 3 мм. Измеренные дробные части поступающей фазы позволяют определять время распространения электромагнитного сигнала между двумя приёмниками с ошибкой не более 10–9 с, что на два порядка точнее по сравнению с другими режимами метода дифференциальной коррекции.