Частные случаи матриц.
1. Если  , то матрица называется квадратной. Её диагональ
, то матрица называется квадратной. Её диагональ  называется главной диагональю, а
называется главной диагональю, а  – побочной диагональю.
– побочной диагональю.
2. Диагональная матрица – это матрица, у которой все ненулевые элементы находятся на главной диагонали, т.е.  .
.
3. Диагональная матрица вида  называется скалярной.
называется скалярной.
4. Скалярная матрица с единичными элементами на главной диагонали называется единичной. Обозначается  или
или  , где
, где  – ее порядок.
– ее порядок.
5. Матрица размера  , у которой все элементы равны нулю, называется нулевой и обозначается
, у которой все элементы равны нулю, называется нулевой и обозначается  .
.
6. Если  , то матрица называется строкой, или матрица-строка, или строка. Если
, то матрица называется строкой, или матрица-строка, или строка. Если 
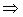 столбцовая = матрица-столбец = столбец.
столбцовая = матрица-столбец = столбец.
Определение 2. Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают.
2о. Операции над матрицами и их свойства.
Определение 3. Суммой матриц  и
и  (т.е. имеющих одинаковые порядки) называется матрица
(т.е. имеющих одинаковые порядки) называется матрица 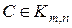 :
:  .
.
Обозначение:  .
.
Замечание. Сумма матриц – алгебраическая операция.
Пример.
 .
.
Свойства (сложения матриц).
1) Коммутативность сложения, т.е., 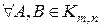 справедливо
справедливо  .
.
2) Ассоциативность сложения, т.е.,  справедливо
справедливо  .
.
3)  .
.
4)  . При этом, если
. При этом, если 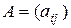 , то
, то  . Матрица
. Матрица  называется противоположной к
называется противоположной к  и обозначается
и обозначается  .
.
Доказательство свойств – самостоятельно прямыми вычислениями.
Теорема 1. Множество  относительно сложения образует абелеву группу.
относительно сложения образует абелеву группу.
Доказательство следует из свойств 1)–4).
Определение 4. Произведением элемента 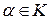 на матрицу
на матрицу  называется матрица
называется матрица 
Обозначение:  .
.
Операция, сопоставляющая  и
и  их произведение
их произведение  называется умножением элемента кольца на матрицу.
называется умножением элемента кольца на матрицу.
Свойства (умножения матрицы на элемент кольца).
 выполняется
выполняется
1)  .
.
2)  .
.
3)  .
.
4)  .
.
Доказательство свойств – самостоятельно прямыми вычислениями.
Замечание. Разность  двух прямоугольных матриц
двух прямоугольных матриц  и
и  определяется равенством
определяется равенством  .
.
Определение 5. Произведением матриц 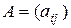 размера
размера  и
и 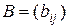 размера
размера  называется матрица
называется матрица  размеров
размеров  такая, что каждый элемент
такая, что каждый элемент  .
.
Обозначение:  .
.
Операция произведения  на
на  называется перемножением этих матриц.
называется перемножением этих матриц.
Из определения следует, что элемент матрицы  , стоящий в
, стоящий в  –ой строке и
–ой строке и  –ом столбце, равен сумме произведений элементов
–ом столбце, равен сумме произведений элементов  –ой строки матрицы
–ой строки матрицы  на
на  –ый столбец матрицы
–ый столбец матрицы  .
.
Примеры.
1)  ,
,
2)  .
.
Таким образом, две матрицы можно перемножать, если число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  . Тогда матрица
. Тогда матрица  называется согласованной с
называется согласованной с  . Из согласованности
. Из согласованности  с
с  не следует согласованность
не следует согласованность  с
с  . Если даже условие согласования выполняется, то в общем случае
. Если даже условие согласования выполняется, то в общем случае  .
.
Свойства (умножения матриц).
1) Ассоциативность умножения матриц, т.е., 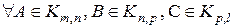 справедливо
справедливо  .
.
Доказательство. Из определения 5 следует, что элемент 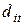 матрицы
матрицы  равен
равен  , а элемент
, а элемент  матрицы
матрицы  равен
равен  . Равенство
. Равенство 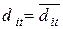 следует из возможности изменения порядка суммирования.
следует из возможности изменения порядка суммирования.
2) Дистрибутивность сложения относительно умножения, т.е.,
 ,
,  .
.
 ,
,  .
.
Доказательство следует из определения суммы и произведения матриц.
3)  .
.
Доказательство. Пусть  , и
, и  . Тогда
. Тогда 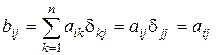 . Здесь
. Здесь  – символ Кронекера.
– символ Кронекера.
 .
.
4)  .
.
5) 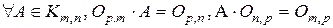 .
.
Доказательство свойств 4)-5) проводится аналогично свойству 3).
6)  .
.
Теорема 2. Множество  квадратных матриц порядка
квадратных матриц порядка  над кольцом
над кольцом  относительно операций сложения матриц и умножения матриц образует кольцо с единицей.
относительно операций сложения матриц и умножения матриц образует кольцо с единицей.
Доказательство. Из теоремы 1  – абелева группа. Так как любые матрицы из
– абелева группа. Так как любые матрицы из  согласованы
согласованы 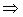 умножение определено. Дистрибутивность и ассоциативность умножения следует из свойств 2) и 1). Свойство 3) демонстрирует наличие единицы.■
умножение определено. Дистрибутивность и ассоциативность умножения следует из свойств 2) и 1). Свойство 3) демонстрирует наличие единицы.■
Замечание. В общем случае произведение матриц не коммутативно. Например,
 .
.
Но из свойств 4) и 5) 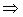 умножение квадратной матрицы на
умножение квадратной матрицы на  и
и  коммутирует. Также коммутирует умножение квадратной матрицы на скалярную.
коммутирует. Также коммутирует умножение квадратной матрицы на скалярную.
3о. Блочные матрицы.
Пусть матрица  при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых является матрицей меньших размеров и называется блоком исходной матрицы. В этом случае
при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых является матрицей меньших размеров и называется блоком исходной матрицы. В этом случае  рассматривается как некоторая новая, блочная матрица
рассматривается как некоторая новая, блочная матрица  , элементами которой являются блоки
, элементами которой являются блоки  указанной матрицы (
указанной матрицы ( – элементы матрицы, поэтому
– элементы матрицы, поэтому  заглавное). Здесь
заглавное). Здесь  – номер блочной строки,
– номер блочной строки,  – столбца.
– столбца.
Например, если
 , то
, то  ,
,
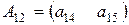 ,
,  ,
,  .
.
Замечательным является факт, что операции с блочными матрицами совершаются по тем же правилам, что и обычными, только в роли элементов выступают блоки. Действительно, если  , то
, то  , где
, где  вычисляется по обычному правилу умножения матрицы на число. Аналогично, если
вычисляется по обычному правилу умножения матрицы на число. Аналогично, если 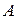 и
и  имеют одинаковые порядки и одинаковым образом разбиты на блоки, то сумме
имеют одинаковые порядки и одинаковым образом разбиты на блоки, то сумме  отвечает блочная матрица
отвечает блочная матрица  :
:  .
.
Для умножения  на
на  необходимо согласовать их разбиение на блоки, т.е. число столбцов каждого блока
необходимо согласовать их разбиение на блоки, т.е. число столбцов каждого блока  равно числу строк блока
равно числу строк блока 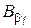 . Тогда
. Тогда  .
.
Для доказательства необходимо расписать правую и левую части в терминах обычных элементов матриц 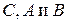 . Пусть
. Пусть  . Если
. Если  , то
, то  и
и 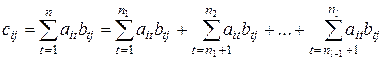 , откуда следует, что
, откуда следует, что
 , что и требовалось доказать.
, что и требовалось доказать.
Пример. Пусть 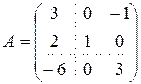 ,
,  , т.е.,
, т.е.,
 ,
,  ,
,
где
 ,
,
 .
.
Тогда 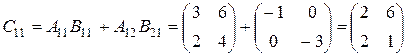 . Аналогично находятся остальные
. Аналогично находятся остальные  . В результате получаем
. В результате получаем
 .
.
В качестве применения блочных матриц рассмотрим
Определение 6. Прямой суммой квадратных матриц 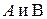 порядков
порядков  соответственно называется квадратная матрица
соответственно называется квадратная матрица  порядка
порядка  :
:  .
.
Обозначение:  .
.