Понятие индексов. Классификация индексов.
Индекс – относительный показатель, выражающий соотношение величин какого-либо явления во времени, пространстве или в сравнении с эталоном, планом. Индекс показывает во сколько раз уровень явления в одних условиях больше или меньше уровня такого же явления в других условиях.
Обозначения:
I – общий индекс;
i – индивидуальный индекс;
q – объем производства (продаж) в натуральных единицах;
p – цена единицы продукции;
pq – товарооборот (стоимость);
z – себестоимость единицы продукции;
zq – затраты;
w – выработка на единицу времени (1 работника);
t – трудоемкость;
T=tq – общие затраты труда.
Классификация индексов.
1. По характеру индексируемой величины:
- Качественные (индексируемая величина – показатель в расчете на единицу);
- Количественные (объемные).
2. По охвату единиц совокупности:
- индивидуальные – изучают 1 ед. (товар и т.д.);
- общие (сводные) – изучают группу товаров.
3. Общие индексы.
· По форме: агрегатные и средние.
· По составу явлений: переменного и фиксированного состава.
· По базе сравнения: динамические и территориальные.
· По виду весов: с постоянными и переменными весами.
Индивидуальные и общие индексы.
Индивидуальные индексы совпадают с относительными показателями динамики сравнения или плана.
; 
; 
; 
; 
.
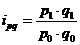Период, уровень которого сравнивается, называется отчетным, или текущим периодом и обозначается знаком «1», а период, с уровнем которого проводится сравнения, называется базисным и обозначается подстрочным знаком «0» или «пл», если сравнение производится с планом.
;(индекс цен) 
;(индекс себестоимости) 
(индекс трудоемкости)
; 
; 
.
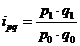Индекс выражается в виде коэффициента, когда база для сравнения принимается за единицу, и в процентах, когда база для сравнения принимается за 100. Если в результате вычислений полученный индекс больше 1 или 100%, то это указывает на рост явления, если же меньше 1 или 100% - на снижение уровня изучаемого явления.
Общие индексы.
Общие индексы применяются для изучения динамики различных показателей по группе товаров или для изучения динамики одного товара, реализуемого в различных местах. Так как складывать объемы продаж и цены различных товаров нельзя, то необходимо привести их к сопоставимому виду. Для этого умножают данный показатель на общий соизмеритель, этот соизмеритель называется весом индекса.
Общие индексы в статистике наиболее часто строятся в агрегатной форме.
Агрегатный индекс – это соотношение сумм произведений индексируемой величины на вес, взятых в соответствующих периодах.
Примеры агрегатных индексов:
1. Индекс цен
этот индекс показывает, как изменяется стоимость товарной группы под влиянием изменения цен каждого товара.
- на сколько процентов.
Разность числителя и знаменателя показывает абсолютное изменение стоимости или эффект (перерасход) покупателя от изменения цен.
2. Индекс физического объема.
показывает, как изменяется стоимость товарной группы под влиянием изменения объемов производства (объема продаж).
- на сколько процентов.
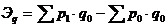- показывает абсолютный эффект изменения от изменения объема продаж.
3. Индекс товарооборота (стоимости).
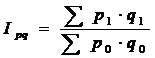
- на сколько процентов.
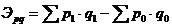- показывает, как изменяется стоимость товарной группы фактически в отчетном периоде по сравнению с базисным.
Взаимосвязь индексов имеет вид:
|
4. Индекс себестоимости.
показывает как изменяются затраты в зависимости от изменения себестоимости.
5. Индекс физического объема.
показывает как изменяются затраты под влиянием изменения объемов производства.
6. Индекс затрат.
показывает, как изменяются затраты фактически.
|
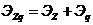
Правило построения агрегатного индекса:
Если индексируемая величина является качественной, то вес берется в отчетном периоде, если она является количественной, то вес берется в базисном периоде.
ПРИМЕР: Имеются данные по двум товарам:
| Вид товара | Цена 1 ед., руб. | V продаж, тыс. ед. | Стоимость, тыс. руб. | ||||
| Базисный, pо | Отчетный р1 | Базисный q0 | отчетный q1 | p0q0 | p1q1 | p0q1 | |
| А, шт. В, кг | |||||||
| ИТОГО | -- | -- | -- | -- |
Найти общие индексы – Ip; Iq; Ipq.
= +5,9%
=3368-3180=188 тыс. руб.
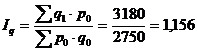
= +15,6%
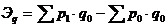=3180-2750=430 тыс. руб.
Ip*Iq=Ipq= 1,156*1,059=1,224
= +22,4%
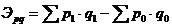=618 тыс. руб.
Вывод: В отчетном периоде по сравнению с базисным стоимость данной товарной группы фактически возросла на 22,4% или 618 тыс. руб. Под влиянием изменения цен каждого товара она увеличилась на 5,9% или на 188 тыс. руб., а под влиянием изменения объемов продаж она увеличилась на 15,6%, или 430 тыс. руб.
Средние индексы.
Во многих случаях из-за отсутствия исходных данных невозможно рассчитать индекс в агрегатной форме, в этом случае применяются средние индексы.
Средний индекс – это средневзвешенная величина из индивидуальных индексов каждого товара. При этом, если показатель качественный, то применяется средняя гармоническая, если количественный, то средняя арифметическая.
Средние индексы являются модификацией агрегатных.
, где
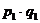- стоимость товара в отчетном периоде;
- индивидуальный индекс цен;
;
; 
; 
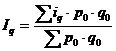Индексы средних величин и их субиндексы: постоянного состава и структурных сдвигов
Рассмотрим некоторые индексы качественных показателей:
1. Индекс выработки
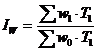- он показывает, как изменяется объем продукции в целом по предприятию под влиянием изменения выработки каждого вида продукции.
2. Индекс трудоемкости
- он показывает, как изменяются затраты труда в целом по предприятию под влиянием изменения трудоемкости каждого вида продукции.
Если какой-либо один вид продукции производится или реализуется в различных местах, то для изучения динамики среднего качественного показателя по этому виду продукции (p, w, t, z) применяются индексы:
· переменного состава;
· фиксированного состава;
· структурных сдвигов.
Динамика среднего качественного показателя складывается под влиянием:
1. Изменения этого показателя в каждом месте.
2. Доли каждого места в общем объеме производства или реализации. Эта доля называется структурой.
; 
;
1. Индекс переменного состава.
;
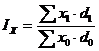2. Индекс фиксированного состава.
;
3. Индекс структуры.
;
|
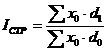1. Индекс переменного состава показывает, как изменяется в среднем индексируемая величина под влиянием изменения самой этой величины и структуры.
2. Индекс фиксированного состава показывает, как изменяется в среднем индексируемая величина под влиянием только одного фактора (самой индексируемой величины в каждом месте производства или реализации).
3. Индекс структурных сдвигов показывает, как изменяется в среднем индексируемая величина под влиянием структуры.