ЧОУ ВПО «Институт экономики, управления и права (г. Казань)»
Факультет менеджмента и инженерного бизнеса
Кафедра ПМ
Погодин Д.В.
ОСНОВЫЭЛЕКТРОТЕХНИКИ И ЭЛЕКТРОНИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И КОНТРОЛЬНЫЕ ЗАДАНИЯ ДЛЯ СТУДЕНТОВ
ЗАОЧНОЙ ФОРМЫОБУЧЕНИЯ
ОБУЧАЮЩИХСЯ ПО НАПРАВЛЕНИЮ
221400.62 – Управление качеством
Набережные Челны – 2014
Контрольная работа №1
Исследование электрической цепи постоянного тока
Цель работы: экспериментальная проверка основных законов для линейных электрических цепей постоянного тока.
Программа работы
1. Выполнить опытную проверку законов Кирхгофа для одной из схем, изображенных на рис 1. Значения параметров схемы указаны в таблице 1 (вариант схемы задается преподавателем). Для этого собрать схему из шести сопротивлений и двух источников ЭДС. В каждую ветвь включить амперметр и включить вольтметры для измерения напряжения каждой ветви.
 Примечание: элементы схемы выводящего на экран из окошка
Примечание: элементы схемы выводящего на экран из окошка  ; амперметры и вольтметры из окошка.
; амперметры и вольтметры из окошка.
При установке значений сопротивлений установить единицу измерения «Ом». Для этого дважды нажав на «мышку», изменить размерность с «КΩ» на «Ω».
2. Выполнить опытную проверку принципа наложения.
3. Выполнить опытную проверку принципа взаимности.
Пояснения к работе
1. Законы Кирхгофа являются основными соотношениями, на которых базируется расчет электрических цепей.
Первый закон Кирхгофа:
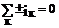 (1)
(1)
Алгебраическая сумма токов, сходящихся в теле цепи, равна нулю.
Правило знаков. При расчете токораспределения в электрической цепи произвольно выбираются условные положительные направления токов в ветвях. Эти направления указываются на схеме стрелками. Ток, вычисленный (или измеренный) в выбранном направлении, может быть либо положительным, либо отрицательным, т.е. 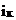 – алгебраические числа. Если при составлении уравнений по первому закону Кирхгофа токи, утекающие от узла считать положительными, то токи, подтекающие к узлу, должны браться с дополнительным знаком «минус».
– алгебраические числа. Если при составлении уравнений по первому закону Кирхгофа токи, утекающие от узла считать положительными, то токи, подтекающие к узлу, должны браться с дополнительным знаком «минус».
|
|
Второй закон Кирхгофа:
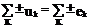 (2)
(2)
Алгебраическая сумма падений напряжений в любом замкнутом контуре равняется алгебраической сумме э.д.с. источников, входящих в тот же контур, или сумма напряжений вдоль замкнутого контура равна нулю.
U1+U2+U3+U4=0
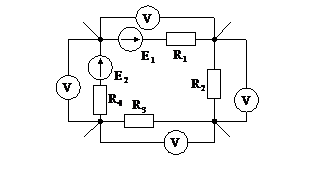
Рис.1. Схема включения приборов




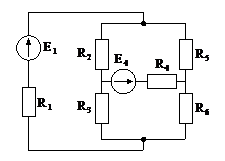
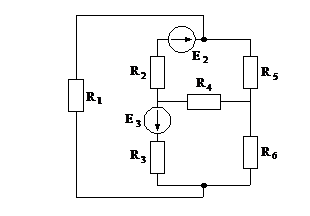
Рис. 2. Схемы электрические (1-6)
Правило знаков. При составлении уравнений по второму закону Кирхгофа выбирается направление обхода контура. Напряжение uk записывается в левую часть равенства, а э.д.с. ek – в правую. При этом uk и ek должны быть взяты с дополнительными знаками «плюс», если их стрелки совпадают с дополнительными знаками «минус», если стрелки противоположны направлению обхода.
Проверка законов Кирхгофа в данной работе заключается в следующем:
а) собирается конкретная цепь. Варианты схем приведены на рис. 2. Номер схемы и величины э.д.с. задаются преподавателем;
б) на электрической схеме цепи стрелками указываются выбранные направления вычисления токов;
в) с помощью амперметра и вольтметра производится измерение всех токов и напряжений (см. рис.3).
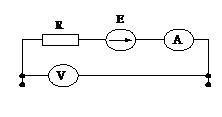
Рис. 3.
г) составляются уравнения для всех узлов и контуров цепи по законам Кирхгофа в буквенных обозначениях токов, напряжений и э.д.с. Затем подставляются измеренные значения этих величин и проверяется справедливость равенств (1) и (2);
|
|
2. Принцип наложения формулируется следующим образом: ток в К-ой ветви: равен алгебраической сумме токов, вызываемых в этой ветви каждой из э.д.с. схемы в отдельности.
Принцип наложения используется в методе расчета, получившем название метода наложения.
Опытная проверка принципа наложения производится в следующем порядке:
а) в цепи, собранной при выполнении пункта 1, отключается один из источников э.д.с., а по месту его действия ставится закоротка (внутреннее сопротивление источника считается равным нулю). Производится измерение токов 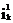 во всех ветвях;
во всех ветвях;
б) проделывается то же самое, что и в пункте 2а, при возвращенном на прежнее место первом источнике и отсоединенном (вместо второго источника ставится закоротка).
Записываются значения токов 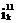 .
.
в) по измеренным 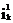 и
и 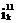 рассчитываются токи
рассчитываются токи 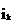 во всех ветвях при действии обоих источников. Согласно принципу наложения
во всех ветвях при действии обоих источников. Согласно принципу наложения 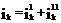
Полученные значения нужно сравнить с измеренными ранее в пункте 1 токами 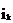 и убедиться в справедливости принципа наложения. Для того чтобы внутреннее сопротивление источников можно было считать равным нулю, необходимо при всех измерениях поддерживать на зажимах каждого источника, включенного в схему, неизменное напряжение.
и убедиться в справедливости принципа наложения. Для того чтобы внутреннее сопротивление источников можно было считать равным нулю, необходимо при всех измерениях поддерживать на зажимах каждого источника, включенного в схему, неизменное напряжение.
Токи 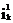 и
и 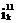 – алгебраические числа; определение их знаков производится в соответствии с правилами, описанными в пункте 1.
– алгебраические числа; определение их знаков производится в соответствии с правилами, описанными в пункте 1.
3. Принцип взаимности формулируется следующим образом; для любой линейной цепи ток, в К-й ветви ikm, вызванный эдс em, находящейся в m – ой ветви, равен току в m – ой ветви imk вызванному эдс ek (численно равной эдс em), находящейся в К-ой ветви.
|
|
ikm= imk
Таблица измерений и вычислений
| №№ ветвей | Примечание | |||||||
| e | В | |||||||
| U | В | |||||||
| i | А | |||||||
| i1 | А | |||||||
| i11 | А | |||||||
| i1+i11 | А | |||||||
| em | В | |||||||
| ikm | А | |||||||
| ek | В | |||||||
| imk | А |
Контрольные вопросы
1. Как формулируются законы Кирхгофа?
2. Что означают стрелки тока, напряжения, ЭДС?
3. Как формулируются правила знаков при составлении уравнений Кирхгофа?
4. Как с помощью вольтметра магнитоэлектрической системы определить величину и знак потенциала любой точки цепи по отношению к точке, потенциал которой принят за нулевой?
5. Как формулируется принцип взаимности?
6. В чем состоит опытная проверка принципа взаимности?
7. Как формулируется принцип наложения?
8. В чем состоит опытная проверка принципа наложения?
9. Можно ли определить мощность, выделяемую в сопротивлении, пользуясь принципом наложения?
10. Как экспериментально определить параметры схемы эквивалентного генератора?
11. В чем заключается метод контурных токов?
12. Как определяется собственные и взаимные сопротивления?
Таблица 1
| Варианты | Ei | Ej | R1 | R2 | R3 | R4 | R5 | R6 |
| В | В | Ом | Ом | Ом | Ом | Ом | Ом | |
Контрольная работа №2
Исследование фазового резонанса в цепи с последовательным соединением активного, индуктивного и емкостного сопротивлений.
Цель работы: уяснить условия получения резонанса напряжений, экспериментально исследовать явление резонанса напряжений в зависимости от изменения либо реактивного сопротивления, либо частоты исследуемой цепи.
Основные теоретические положения.
Резонанс напряжений называется такой пассивной электрической цепи переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений, при котором входное реактивное сопротивление равно нулю. При резонансе напряжений напряжение на входе цепи совпадает по фазе с током, т.е.
j = yu - yi =0
Условие фазового резонанса через параметры последовательного контура записывается в виде:
хL=xC или 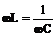 (1)
(1)
Из условия (1) следует, что резонанса можно достичь, изменяя индуктивность, емкость и частоту входного сигнала ¦.
Значения параметров определяются по формулам:
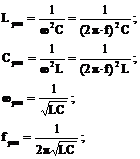
Явление резонанса напряжений характеризуется следующим рядом соотношений.
1.Полное сопротивление цепи 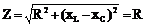 , т.к. х=0; комплекс полного сопротивления
, т.к. х=0; комплекс полного сопротивления
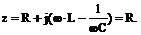
2. Сопротивление цепи минимально, ток в момент резонанса максимален, что следует из закона Ома
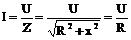
3. Сопротивление каждого из реактивных элементов при резонансе хL=xC не зависит от частоты, называется характеристическим сопротивлением цепи (волновое сопротивление)
xCрез = хLрез; 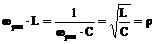
4. Величины напряжений на активном, индуктивном, емкостном сопротивлениях могут быть определены Ua=I×R; UL=I×xL; Uc=I×xC, т.к. хL=xC, то UL=Uc=rI.
Векторная диаграмма тока и напряжений приведена на рис.2.
5. Отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи, при резонансе называют добротностью контура или коэффициентом резонанса.

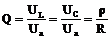
Коэффициент резонанса показывает во сколько раз напряжение на индуктивности или емкости при резонансе больше, чем напряжение приложенное к цепи.
Величина, обратная добротности, называется затуханием цепи
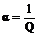
6. Отношение активной мощности к полной, равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности:
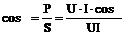
Коэффициент мощности при резонансе напряжений равен 1.
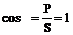
Активная мощность равна полной мощности:
P=S.
На рисунке 1 приведены графики мгновенных значений тока и напряжений.
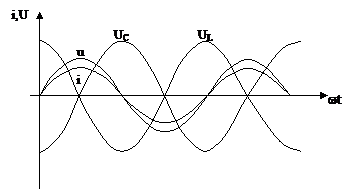
Рис. 1. Графики мгновенных значений тока и напряжений

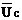
Рис. 2. Векторная диаграмма тока и напряжений в момент резонанса
В рассматриваемой лабораторной работе явление резонанса напряжений получают изменением индуктивности, емкости, частоты входного сигнала.
Программа работы
1. Собрать схему, изображенную на рис.3.

Рис. 3. Схема лабораторной работы
Примечание: элементы схемы выводятся на экран из «окошка»  ; амперметр и вольтметры из окошка
; амперметр и вольтметры из окошка  .
.
Измерительные приборы перевести из режима «ДС» в режим «АС», дважды нажав на мышку.
При установке значений сопротивлений установить единицу измерения «Ом».
Установить значения ЭДС и сопротивлений согласно варианта (таблица 1).
I вариант
Таблица 1
| Вариант | ||||||||||
| E, B | ||||||||||
| R, Ом | ||||||||||
| С, мкФ |
2. Рассчитать значение индуктивности, при которой в цепи будет наблюдаться резонанс напряжений.
3. Изменяя индуктивность катушки индуктивности, провести 7 опытов при различном состоянии цепи, включая и резонансный режим. Опыты следует проводить при неизменном входном напряжении. Результаты занести в таблицу 2.
Таблица 2
| № опы - та | L | Измерено | Вычислено | |||||||||||
| U | I | UR | UC | UL | Z | xL | xC | x | cosj | P | Q | S | ||
| мГн | В | А | В | В | В | Ом | Ом | Ом | Ом | Вт | ВАр | ВА | ||
| … | ||||||||||||||
| … | ||||||||||||||
Расчетные формулы:
Полное сопротивление цепи:
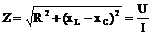
Реактивные сопротивления:
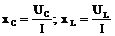
Активная мощность цепи:
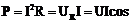
Реактивная мощность цепи:
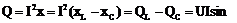
QL - реактивная мощность индуктивности
QC - реактивная мощность емкости
Полная мощность цепи:
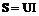
Коэффициент мощности:
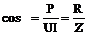
4. По данным опыта и вычисленным параметрам построить кривые зависимостей: UC=f(xL), UL=f(xL); z=f(xL); I=f(xL).
5. Построить векторные диаграммы тока и напряжений для случаев: xL>xC; xL=xC; xL<xC. Все графики и векторные диаграммы выполняются в масштабе.
II вариант
1. Собрать схему, изображенную на рис. 3. Установить значение ЭДС и сопротивлений согласно варианта (таблица 3).
Таблица 3
| Вариант | ||||||||||
| E, B | ||||||||||
| R, Ом | ||||||||||
| L, мГн | 0,1 | 0,15 | 0,1 | 0,2 | 0,15 | 0,1 | 0,3 | 0,2 | 0,18 | 0,12 |
2. Рассчитать значение емкости, при которой в электрической цепи будет наблюдаться резонанс напряжений.
3. Изменяя емкость батареи конденсаторов, провести 6-7 опытов при различном состоянии цепи, включая и резонансный режим. Опыты произвести при неизменном входном напряжении. Результаты занести в таблицу 4.
Таблица 4
| № опы - та | С | Измерено | Вычислено | |||||||||||
| U | I | UR | UC | UL | Z | xL | xC | x | P | Q | S | cosj | ||
| мкФ | В | А | В | В | В | Ом | Ом | Ом | Ом | Вт | ВАр | ВА | ||
| … | ||||||||||||||
| … | ||||||||||||||
4. По данным опыта и вычисленным параметрам построить кривые зависимостей: UC=f(xС), UL=f(xС); z=f(xС); I=f(xС).
5. Построить векторные диаграммы тока и напряжений для случаев: xL>xC; xL=xC; xL<xC.
III вариант
1. Собрать схему, изображенную на рис. 3. Установить значения ЭДС и сопротивлений согласно варианта (таблица 5).
Таблица 5
| Вариант | ||||||||||
| E, B | ||||||||||
| R, Ом | ||||||||||
| L, мГн | 0,1 | 0,12 | 0,18 | 0,2 | 0,16 | 0,2 | 0,3 | 0,25 | 0,15 | 0,22 |
| С, мкФ | 0,22 |
2. Рассчитать значение частоты, при которой в цепи будет наблюдаться резонанс.
3. Изменяя значение частоты, провести 7 опытов при различном состоянии цепи, включая и резонансный режим. Опыты следует проводить при неизменном входном напряжении. Результаты занести в таблицу 6.
Таблица 6
| № опыта | f | Измерено | Вычислено | |||||||||||
| U | I | UR | UC | UL | Z | xL | xC | x | P | Q | S | cosj | ||
| Гц | В | А | В | В | В | Ом | Ом | Ом | Ом | Вт | ВАр | ВА | ||
| … | ||||||||||||||
| … | ||||||||||||||
4. По данным опыта и вычисленным параметрам построить кривые зависимостей: UC=f(w), UL=f(w); z=f(w); I=f(w).
5. Построить векторные диаграммы тока и напряжений для случаев: xL>xC; xL=xC; xL<xC.
Контрольные вопросы:
1. В какой цепи может возникнуть резонанс напряжений? Какое условие необходимо для этого?
2. Какими способами возможно получение в колебательном контуре резонанса напряжений?
3. Что такое добротность контура, как она определяется?
4. При каких условиях напряжения на реактивных элементах цепи могут превышать входное напряжение?
5. Чему равняется коэффициент мощности при резонансе?
6. Какой вид имеют резонансные кривые при изменении частоты?
7. Чему равнялось бы при резонансе полное сопротивление цепи, если бы активное сопротивление R было равно нулю?
8. Как изменится полное сопротивление цепи в момент резонанса напряжений при изменении частоты?
9. Как изменится полная мощность цепи при резонансе напряжений?
10. Как строятся треугольники напряжений, сопротивлений, мощностей?
11. Почему при резонансе при резонансе напряжений ток в цепи максимален?
12. Как определить угол сдвига фаз между напряжением, приложенным к цепи и током, протекающим по ней?
Контрольная работа№3
«Исследование трехфазной электрической цепи