Взаимное расположение прямой и плоскости. Первая главная позиционная задача

ЛЕКЦИЯ 3

Способы задания плоскостей общего положения, проецирующего положения и уровня на эпюре Монжа

Положение плоскости в пространстве и на чертеже можно определить (рисунок 30):

1) тремя точками, не лежащими на одной прямой;

2) прямой и точкой вне ее;

3) двумя пересекающимися прямыми;

4) двумя параллельными прямыми;

5) любой плоской фигурой;

6) следами плоскости.

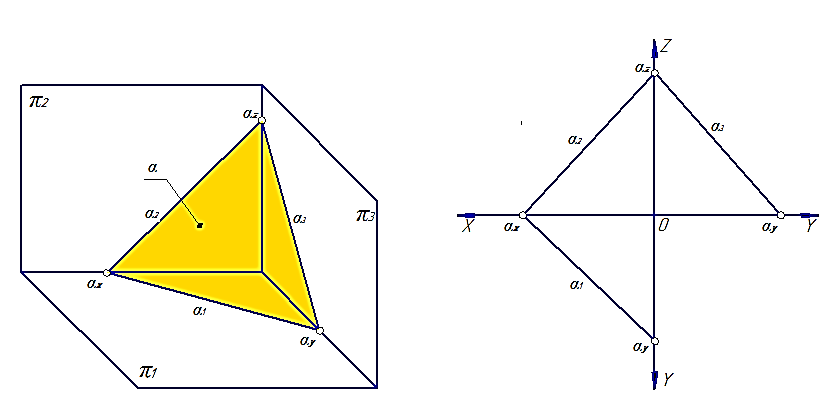
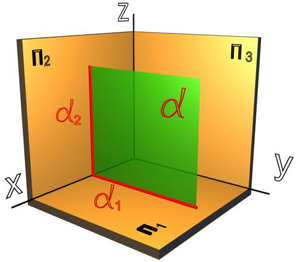
Плоскость, которая занимает общее (произвольное) положение по отношению к плоскостям проекций, называется плоскостью общего положения. Углы наклона этой плоскости к плоскостям проекций произвольные – отличные от 0 и 90°.

 

6)

Рисунок 30. Способы задания плоскости

Линия пересечения плоскости, a с плоскостью проекций называется следом данной плоскости. На рис.30 (6) обозначено:

– a∩π₁ = a₁ – горизонтальный след плоскости a, a₁Ì π₁;

– a∩π₂= a₂ – фронтальный след плоскости a, a₂Ì π₂;

– aÌπ₃= a₃ – профильный след плоскости a, a₃Ì π₃.

Точки пересечения плоскости a с осями проекций называются точками схода следов: a∩0 Х =a _х, a∩0 Y =a _y, a∩0 Z =a _z.

Следует помнить, что при решении задач по начертательной геометрии можно переходить от одного способа задания плоскости к другому т.к. они взаимозаменяемы.

Плоскость частного положения - это плоскость, которая занимает по отношению к плоскостям проекций следующие частные положения: перпендикулярное к одной плоскости проекции и перпендикулярное к двум плоскостям проекций.

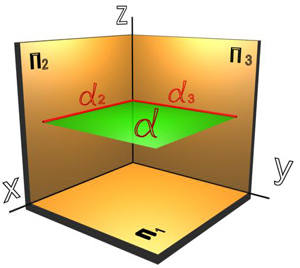
Плоскости, перпендикулярные к двум плоскостям проекции, называются плоскостями уровня (рисунки 31, 32, 33).

 

 

|| П₁ => ₂ || x _1,2

 

 

Рисунок 31. Горизонтальная плоскость уровня

 

 

Все плоскости уровня проецируются в натуральную величину на ту плоскость проекций, которой они параллельны.

 

 

 

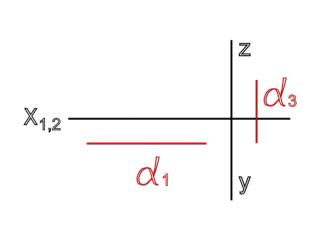
| П₂ => ₁ || x _1,2

 

Рисунок 32. Фронтальная плоскость уровня

 

 

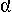|| П₃ => ₁, ₂ _|_ x _1,2

 

Рисунок 33. Профильная плоскость уровня

 

Плоскости, перпендикулярные к одной плоскости проекции, называются проецирующими.

Горизонтально-проецирующая плоскость _|_ П₁ и вырождается в виде прямой на горизонтальной проекции (рисунок 34). Угол 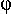– угол наклона плоскости к плоскости проекций П₂.

 

 

 

 

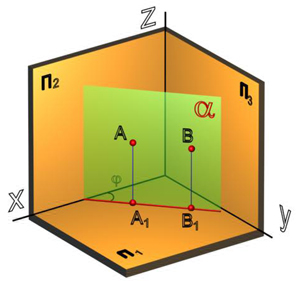
Рисунок 34. Горизонтально-проецирующая плоскость

 

 

Фронтально - проецирующая плоскость 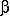_|_ П₂ и вырождается на фронтальной проекции в виде прямой (рисунок 35). Угол 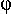– угол наклона плоскости 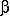к плоскости проекций П₁.

 

 

 

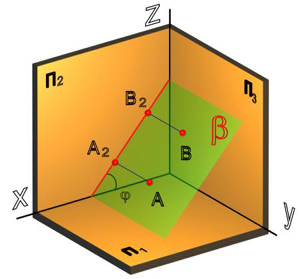
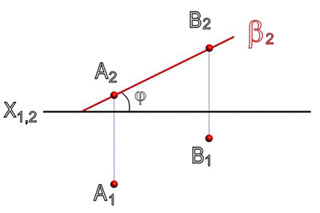
Рисунок 35. Фронтально-проецирующая плоскость

 

 

Профильно - проецирующая плоскость 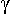_|_ П₃ и вырождается на профильной проекции в виде прямой (рисунок 36). Угол 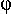– угол наклона плоскости 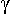к плоскости проекций П₂.

 

 

 

 

Рисунок 36. Профильно-проецирующая плоскость

 

Взаимное расположение прямой и плоскости. Первая главная позиционная задача

Возможны следующие три случая относительного расположения прямой и плоскости:

- прямая принадлежит плоскости;

- прямая параллельна плоскости;

- прямая пересекает плоскость;

- прямая перпендикулярна плоскости.

На основании свойства плоскости: если прямая линия соединяет две точки данной плоскости, то такая прямая всеми своими точками лежит в этой плоскости. Рассмотрим принадлежность прямой плоскости на примере построения главных линий плоскости.

Главные линии плоскости полностью определяют положение плоскости в пространстве и их часто используют для решения задач в начертательной геометрии. К главным линиям плоскости относятся прямые, лежащие в данной плоскости и параллельные одной из плоскостей проекций. Иначе такие прямые называют линиями уровня плоскости.

Горизонтальной линией уровня плоскости — горизонталью плоскости — называется прямая, лежащая в данной плоскости и параллельная плоскости проекций П₁ (рисунок 37).

Фронтальная проекция любой горизонтали перпендикулярна линиям связи (h₂ _|_ A₂A₁ ), поэтому построение горизонтали плоскости (АВС) начинается с ее фронтальной проекции: h₂ _|_ A₂A₁; h₂ A₂B₂ = D₂; h₂ B₂C₂ = E₂

D₂D₁ A₁B₁ = D₁; E₂E₁ B₁C₁ = E₁; h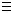₁ D₁E₁.

Все горизонтали данной плоскости параллельны друг другу, так как каждая из них может быть получена как линия пересечения данной плоскости с плоскостью, параллельной П₁.

Фронтальной линией уровня плоскости — фронталью плоскости — называется прямая, лежащая в данной плоскости и параллельная плоскости проекций П₂ (рисунок 38).

 

 

Рисунок37. Построение горизонтали плоскости

Рисунок 38. Построение фронтали плоскости

 

Горизонтальная проекция любой фронтали перпендикулярна линиям связи (f₁ _|_ A₁A₂), поэтому построение фронтали плоскости (a || b) начинается с ее горизонтальной проекции: f₁ _|_ A₁A₂; f₁ a₁ = A₁; f₁ b₁ = B₁;

A₁A₂ a₂ = A₂; B₁B₂ b₂ = B₂; f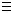₂ A₂B₂.

Все фронтали данной плоскости параллельны друг другу, так как каждая из них может быть получена как линия пересечения данной плоскости с плоскостью, параллельной П₂.

Из стереометрии известно: если прямая параллельна плоскости, то она параллельна одной из прямых, лежащих в этой плоскости.

На эпюре (рисунок 39) параллельность прямой m и плоскости ABC доказывается тем, что m'' // a'', m' // a'; прямая a принадлежит плоскости ABC.

 

 

Рисунок 39. Построение прямой m // плоскости ABC

Если прямая пересекает плоскость, то решается задача по нахождению точки встречи прямой с плоскостью. Определение точки встречи прямой с плоскостью – первая главная позиционная задача - относится к элементарной задаче, но ее значение для решения самых различных, более сложных задач, трудно переоценить. Первая ГПЗ входит как составная часть (фрагмент) в алгоритм решения широкого круга как позиционных, так и метрических задач. Решение этой задачи легко сводится к простейшей задаче по определению линии пересечения двух плоскостей, из которых одна — проецирующая, с последующим определением второй проекции точки, принадлежащей плоскости, если известна одна из ее проекций. Для этого, достаточно прямую заключить во вспомогательную проецирующую плоскость.

Пример. Определить точку К пересечения данной прямой а с плоскостью . Определить видимость прямой. Решение задачи выполняется в три этапа. Алгоритм решения представлен на рисунке 40.

 

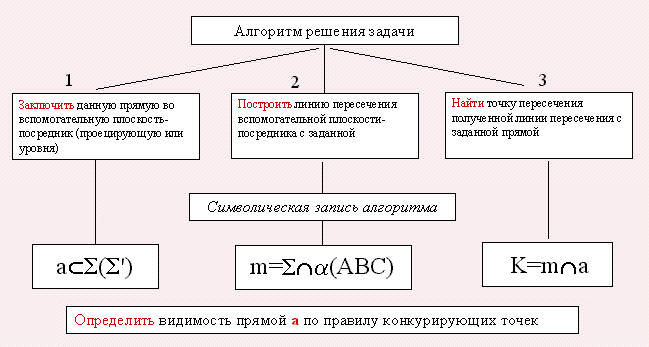
Рисунок 40. Алгоритм решения 1-ой ГПЗ

 

Рассмотрим применение данного алгоритма при решении задачи на построение точки К пересечения прямой а с плоскостью . Возможны три варианта условия данной задачи:

- прямая а - общего положения, плоскость - проецирующая (или уровня);

- прямая а - проецирующая, плоскость - общего положения;

- прямая а - общего положения, плоскость - общего положения.

Решение первых двух задач можно выполнить, не применяя алгоритма, так как один из заданных образов частного положения.

В первом случае (рисунок 41) плоскость (АВС) – горизонтально - проецирующая.

Поэтому горизонтальная проекция К ' искомой точки К определяется как точка пересечения линейной проекции А'В'С' плоскости с горизонтальной проекцией а ' данной прямой а.

Фронтальная проекция К " точки К строится из условия принадлежности точки К прямой а.

Во втором случае прямая а - фронтально-проецирующая (рисунок 42).

Поэтому фронтальные проекции любой ее точки, а также и искомой К пересечения а с плоскостью (АВС), совпадает с ее вырожденной проекцией (a " совпадает с К "). Построение горизонтальной проекции К ' точки К выполняется из условия принадлежности точки К плоскости : точка К принадлежит плоскости , так как она принадлежит ее прямой A₁ (К ' находится как точка пересечения прямой A ' 1 ' с прямой а ').

Видимость прямой а в этих задачах решается просто - с помощью реконструкции данных образов (по наглядности).

 

Рисунок 41. Решение задачи на пересечение проецирующей плоскости с прямой общего положения

Рисунок 42.Решение задачи на пересечение проецирующей прямой с плоскостью общего положения

В третьем, общем, случае построение искомой точки К пересечения прямой а с плоскостью (c // d) выполнено по описанному алгоритму (рисунок 43).

1) прямую а заключают во вспомогательную горизонтально – проецирующую плоскость - посредник S (S ^/);

2) строят прямую m пересечения плоскостей (c // d) и S (S ^/). Фронтальную проекцию m '' строят из условия ее принадлежности данной плоскости (m и a имеют общие точки 1 и 2);

3) находят точку K '', как результат пересечения a '' с m '', а K ' строят по принадлежности прямой m '. Точка K (K '', K ') - искомая точка пересечения прямой a с плоскостью (c // d).

 

S /

 

а) б)

 

Рисунок 43. а) исходное условие задачи; б) решение задачи.

Задачу заканчивают определением видимости прямой по правилу конкурирующих точек. Так, на плоскости П₁ видимость определена с помощью горизонтально конкурирующих точек 1 и 3 (1 ^/ 3 ^/), где точка 1 принадлежит плоскости , а точка 3 - прямой a. Точка 3 расположена над точкой 1, поэтому точка 3 и прямая a в этом участке на плоскости П₁ будет видима.

На фронтальной плоскости видимость может быть определена или с помощью пары фронтально-конкурирующих точек, или по реконструкции данных образов (при восходящей плоскости видимость одинаковая на плоскостях П₁ И П₂)

Если прямая линия пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня плоскости.

Пример. На плоскость, заданную треугольником ABC, необходимо опустить перпендикуляр из точки К. Построение выполняют следующим образом (рисунок 44). На плоскости проводят горизонталь h (h'', h') и фронталь f (f ', f''). Затем из заданных проекций K' и K'' точки К опускают перпендикуляры соответственно на h' и f ''. Прямая, проведенная таким образом из точки К, будет перпендикулярна плоскости треугольника ABC (так как прямая, перпендикулярная плоскости должна быть перпендикулярна двум прямым, лежащим в этой плоскости).

 

Рисунок 44. Построение перпендикуляра к плоскости

2. Взаимное расположение двух плоскостей. Вторая главная позиционная задача, решение и определение видимости.

 

Две плоскости в пространстве могут быть либо взаимно параллельными, пересекающимися (рисунок 45) либо перпендикулярными.

Параллельные плоскости. Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Искомая плоскость , параллельная заданной плоскости , определена прямыми a ₁ и b ₁ соответственно параллельными a и b заданной плоскости и проходящими через произвольную точку пространства A.

 

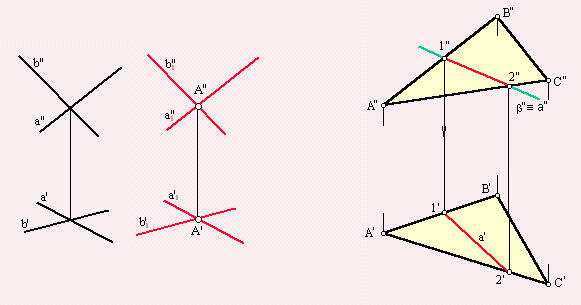
Рисунок 45. Взаимное положение плоскостей

 

Пересекающиеся плоскости. Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две точки, общие обеим плоскостям. Если одна из пересекающихся плоскостей занимает частное положение, то ее вырожденная проекция b '' включает в себя и проекцию a '' линии a пересечения плоскостей. Горизонтальную проекцию a' прямой a строят по двум общим с плоскостью точкам 1 и 2.

Для определения точек линии пересечения обе заданные плоскости и пересекают двумя вспомогательными (параллельными между собой) плоскостями-посредниками. Некоторое упрощение можно достичь, если вспомогательные плоскости проводить через прямые, задающие плоскость.

Пример. На рисунке 46 мы видим аксонометрическое изображение решения задачи на определение линии MN пересечения двух плоскостей ABC и DEK.

Плоскость задана (ABC), плоскость задана (DEK). Точки M и N, определяющие искомую линию пересечения двух данных плоскостей найдем как точки пересечения каких-либо двух сторон (рассматриваем их как две прямые) треугольника ABC с плоскостью другого треугольника DEK, т.е. дважды решим позиционную задачу на определение точки пересечения прямой с плоскостью по рассмотренному выше алгоритму. Выбор сторон треугольников произволен, так как только построением можно точно определить, какая действительно сторона и какого треугольника пересечет плоскость другого. Выбор плоскости-посредника также произволен, так как прямую общего положения, какими являются все стороны треугольников ABC и DEK, можно заключить в горизонтально - проецирующую или во фронтально - проецирующую плоскости.

 

 

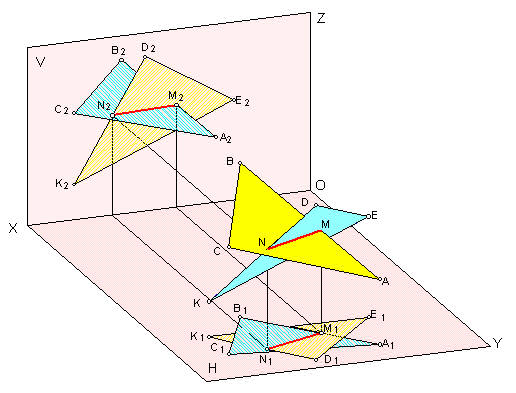
Рисунок 46. Аксонометрическое изображение решения задачи на пересечение плоскостей

Рассмотрим решение этой задачи на плоском чертеже (рисунок 47). Пересекающиеся плоскости заданы многоугольниками - ABC и DEFK. Вспомогательные проецирующие плоскости проводим через какие-либо две из сторон многоугольников.

1) Для построения точки M использована фронтально - проецирующая плоскость - посредник Γ (Γ₂), в которую заключена сторона A₂B₂ треугольника A₂B₂C₂.

2) Строим линию пересечения (на чертеже она задана точками 1₂ и 2₂ плоскости-посредника Γ (Γ₂) и плоскости DEFK.

3) Находим точку M пересечения прямой 1₁ – 2₁ с прямой A₁ B₁.

Найдена одна точка M искомой линии пересечения.

Для построения точки N использована фронтально - проецирующая плоскость Γ (Γ₂^/), в которую заключена сторона A₂C₂ треугольника A₂B₂C₂.

Построения аналогичны предыдущим.

Видимость проекций многоугольников АВС и DEFK на П2 определена с помощью фронтально конкурирующих точек 2 и 7, на П - с помощью горизонтально конкурирующих точек 5 и 6.

 

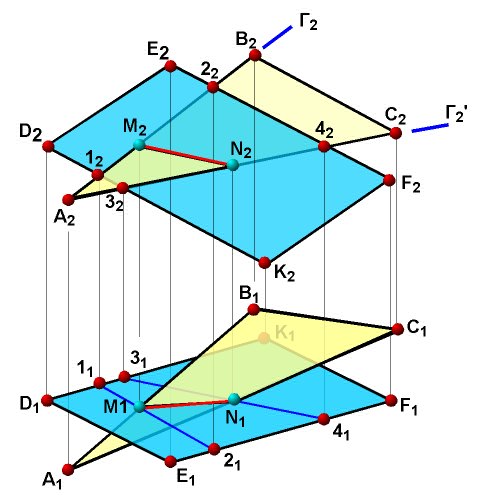
Рисунок 47. Построение линии пересечения плоскостей

Взаимно перпендикулярные плоскости

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Для построения плоскости перпендикулярной к данной достаточно определить прямую линию ей перпендикулярную. Через перпендикуляр к плоскости можно провести множество плоскостей, перпендикулярных данной (рис. 4.20а).

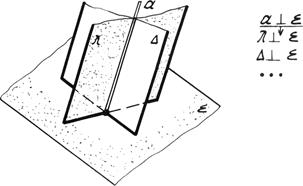
Рис. 4.20а. Взаимно перпендикулярные плоскости

Рассмотрим построение одной из плоскостей, перпендикулярной данной плоскости (c Ç d) (рис. 4.20б).

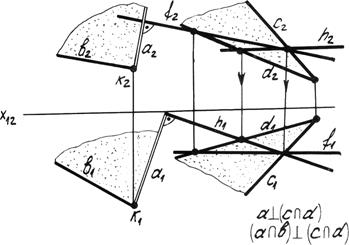
рис. 4.20б. Взаимно перпендикулярные плоскости

Определим горизонталь h и фронталь f¦ данной плоскости. Из произвольной точки K восставим перпендикуляр a на горизонтальной проекции a ₁ ⊥ h ₁, а на фронтальной проекции a ₂ ⊥ f_2. Дополним прямую a до плоскости пересекающейся с ней произвольной прямой b. Плоскость (a Ç b) перпендикулярна плоскости (c Ç d). Запишем правило перпендикуляра:

P₁ ⊥ h₁

P₂ ⊥ f₂

P₃ ⊥ c₃

где: P – обозначение перпендикуляра; h₁ – горизонталь; f - фронталь; с –профильная.