| №
| Вид интеграла
| Способ вычисления
|
| I.
| Табличный интеграл

| Вычисляется с использованием таблицы основных интегралов
= F(x) +С
|
«Почти» табличный интеграл

| Вычисляется с использованием таблицы основных интегралов
= F(x+а) +С
|
«Почти» табличный интеграл
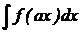
| Вычисляется с использованием таблицы основных интегралов, коэффициент а ставится в знаменатель.
= 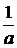 F(аx) +С F(аx) +С
|
| Иногда, при вычислении необходимо преобразовать подынтегральную функцию, раскрыв скобки, разделив почленно, применив тригонометрические формулы.
|
| II.
| Интеграл, содержащий функцию и ее производную

| Вычисляется методом замены переменной
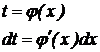 сводится к типу I.
сводится к типу I.
|
| III.
| Произведение многочлена 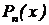 на показательную или тригонометрическую функцию на показательную или тригонометрическую функцию

| Вычисляется методом интегрирования по частям: разбиваем интеграл на части  и и 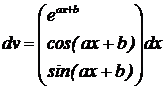 .
Для u вычисляем дифференциал du, для dv первообразную v, применяем формулу .
Для u вычисляем дифференциал du, для dv первообразную v, применяем формулу  .
Второй интеграл .
Второй интеграл 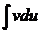 сводится к I, II или XIV. сводится к I, II или XIV.
|
| IV.
| Произведение многочлена 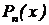 на логарифмическую или обратную тригонометрическую функцию на логарифмическую или обратную тригонометрическую функцию

| Вычисляется методом интегрирования по частям: разбиваем интеграл на части  и и  .
Для u вычисляем дифференциал du, для dv первообразную v, применяем формулу .
Для u вычисляем дифференциал du, для dv первообразную v, применяем формулу  .
Второй интеграл .
Второй интеграл 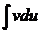 сводится к I, II или XIV. сводится к I, II или XIV.
|
| V.
| Интеграл от рациональной функции, аргументами которой являются 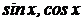
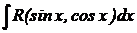
| Применяется универсальная тригонометрическая подстановка
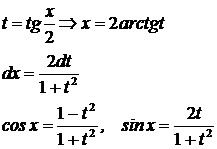 Далее интеграл сводится в виду I, II, XIV, IX.
Далее интеграл сводится в виду I, II, XIV, IX.
|
| VI.
| Интеграл от рациональной функции, являющейся четной относительно 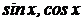
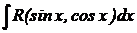 Интеграл от рациональной функции, аргументами которой является
Интеграл от рациональной функции, аргументами которой является 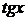
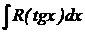
| Применяется подстановка:
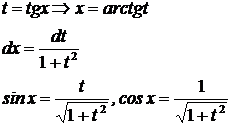 Далее интеграл сводится в виду I, II, XIV, IX.
Далее интеграл сводится в виду I, II, XIV, IX.
|
| VII.
| 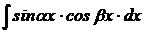
| Применяется формула
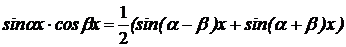
|
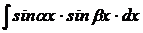
| Применяется формула
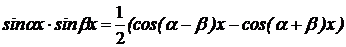
|

| Применяется формула
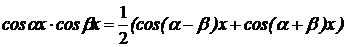
|
| VIII
| 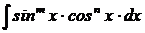
| если m – целое, нечетное, положительное число, делаем подстановку 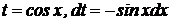 тогда тогда 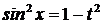 . Получаем интеграл вида I. . Получаем интеграл вида I.
|
если n – целое, нечетное, положительное число, делаем подстановку 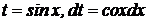 тогда тогда 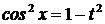 . Получаем интеграл вида I. . Получаем интеграл вида I.
|
если m и n – целые, четные положительные, то применяем формулы
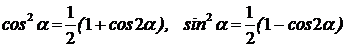 Получаем интеграл вида I. Получаем интеграл вида I.
|
если m+n – целое четное отрицательное число, делаем подстановку 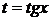 . Получаем интеграл вида I. . Получаем интеграл вида I.
|
| IX.
| 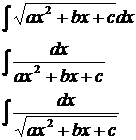

| Выделяем полный квадрат
 ,
делаем замену ,
делаем замену  Получаем интегралы вида I, II.
Получаем интегралы вида I, II.
|
| X.
| 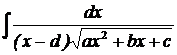
| Делаем подстановку 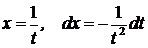 . Получаем интеграл вида IX. . Получаем интеграл вида IX.
|
| XI
| 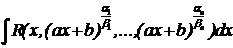
| Делаем замену
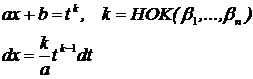 Получаем интегралы вида I, II, XIV.
Получаем интегралы вида I, II, XIV.
|
| XII
| 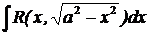
| Делаем тригонометрическую подстановку
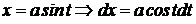 .
Получаем интеграл вида VIII. .
Получаем интеграл вида VIII.
|
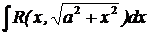
| Делаем тригонометрическую подстановку
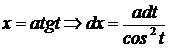 .
Получаем интеграл вида VIII. .
Получаем интеграл вида VIII.
|
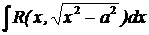
| Делаем тригонометрическую подстановку
 .
Получаем интеграл вида VIII. .
Получаем интеграл вида VIII.
|
| XIII
| Интеграл от дифференциального бинома
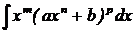
| если р – целое число, делаем замену
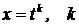 = НОК (знаменателей m и n).
Получаем интегралы вида I, II, XIV. = НОК (знаменателей m и n).
Получаем интегралы вида I, II, XIV.
|
если 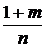 – целое число, делаем замену – целое число, делаем замену
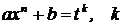 = знаменателю р, = знаменателю р,
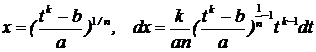 Получаем интегралы вида I, II, XIV.
Получаем интегралы вида I, II, XIV.
|
если 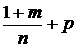 – целое число, делаем замену – целое число, делаем замену
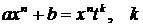 = знаменателю р,
Получаем интегралы вида I, II, XIV. = знаменателю р,
Получаем интегралы вида I, II, XIV.
|
| XIV
| Интеграл от рациональной дроби
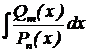
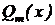 – многочлен степени m, – многочлен степени m, 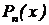 – многочлен степени n. – многочлен степени n.
| Для вычисления интеграла необходимо:
– если дробь неправильная 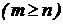 , нужно выделить целую часть, разделив числитель дроби на знаменатель, т.е. представить дробь в виде суммы многочлена и правильной дроби;
– разложить знаменатель дроби на множители;
– разложить правильную дробь на сумму простейших дробей в соответствии с полученными в знаменателе множителями:
множителю , нужно выделить целую часть, разделив числитель дроби на знаменатель, т.е. представить дробь в виде суммы многочлена и правильной дроби;
– разложить знаменатель дроби на множители;
– разложить правильную дробь на сумму простейших дробей в соответствии с полученными в знаменателе множителями:
множителю  соответствует k дробей соответствует k дробей 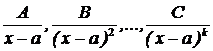 множителю
множителю  соответствует s дробей соответствует s дробей 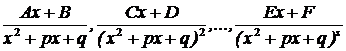 – сумму дробей привести к общему знаменателю;
– приравнять числители дробей;
– приравнять коэффициенты перед одинаковыми степенями х;
– найти неизвестные коэффициенты А, В, С…;
– проинтегрировать получившуюся сумму (получатся интегралы вида I, II, IX). – сумму дробей привести к общему знаменателю;
– приравнять числители дробей;
– приравнять коэффициенты перед одинаковыми степенями х;
– найти неизвестные коэффициенты А, В, С…;
– проинтегрировать получившуюся сумму (получатся интегралы вида I, II, IX).
|
| | | | |


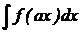
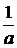 F(аx) +С
F(аx) +С

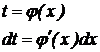 сводится к типу I.
сводится к типу I.
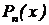 на показательную или тригонометрическую функцию
на показательную или тригонометрическую функцию

 и
и 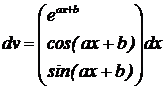 .
Для u вычисляем дифференциал du, для dv первообразную v, применяем формулу
.
Для u вычисляем дифференциал du, для dv первообразную v, применяем формулу  .
Второй интеграл
.
Второй интеграл 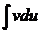 сводится к I, II или XIV.
сводится к I, II или XIV.
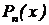 на логарифмическую или обратную тригонометрическую функцию
на логарифмическую или обратную тригонометрическую функцию

 и
и  .
Для u вычисляем дифференциал du, для dv первообразную v, применяем формулу
.
Для u вычисляем дифференциал du, для dv первообразную v, применяем формулу  .
Второй интеграл
.
Второй интеграл 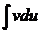 сводится к I, II или XIV.
сводится к I, II или XIV.
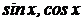
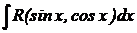
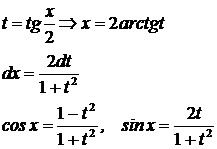 Далее интеграл сводится в виду I, II, XIV, IX.
Далее интеграл сводится в виду I, II, XIV, IX.
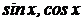
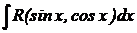 Интеграл от рациональной функции, аргументами которой является
Интеграл от рациональной функции, аргументами которой является 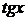
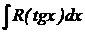
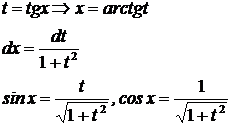 Далее интеграл сводится в виду I, II, XIV, IX.
Далее интеграл сводится в виду I, II, XIV, IX.
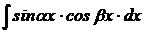
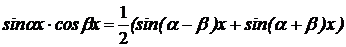
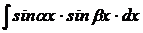
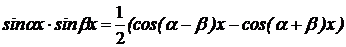

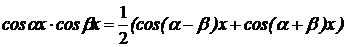
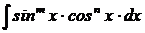
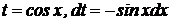 тогда
тогда 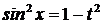 . Получаем интеграл вида I.
. Получаем интеграл вида I.
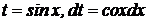 тогда
тогда 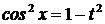 . Получаем интеграл вида I.
. Получаем интеграл вида I.
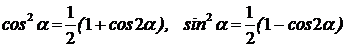 Получаем интеграл вида I.
Получаем интеграл вида I.
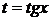 . Получаем интеграл вида I.
. Получаем интеграл вида I.
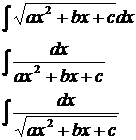

 ,
делаем замену
,
делаем замену  Получаем интегралы вида I, II.
Получаем интегралы вида I, II.
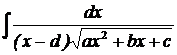
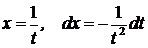 . Получаем интеграл вида IX.
. Получаем интеграл вида IX.
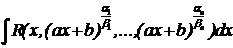
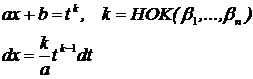 Получаем интегралы вида I, II, XIV.
Получаем интегралы вида I, II, XIV.
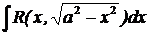
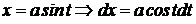 .
Получаем интеграл вида VIII.
.
Получаем интеграл вида VIII.
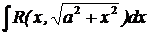
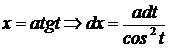 .
Получаем интеграл вида VIII.
.
Получаем интеграл вида VIII.
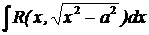
 .
Получаем интеграл вида VIII.
.
Получаем интеграл вида VIII.
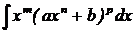
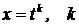 = НОК (знаменателей m и n).
Получаем интегралы вида I, II, XIV.
= НОК (знаменателей m и n).
Получаем интегралы вида I, II, XIV.
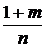 – целое число, делаем замену
– целое число, делаем замену
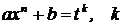 = знаменателю р,
= знаменателю р,
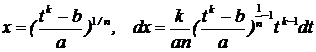 Получаем интегралы вида I, II, XIV.
Получаем интегралы вида I, II, XIV.
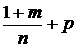 – целое число, делаем замену
– целое число, делаем замену
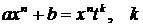 = знаменателю р,
Получаем интегралы вида I, II, XIV.
= знаменателю р,
Получаем интегралы вида I, II, XIV.
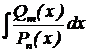
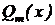 – многочлен степени m,
– многочлен степени m, 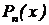 – многочлен степени n.
– многочлен степени n.
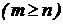 , нужно выделить целую часть, разделив числитель дроби на знаменатель, т.е. представить дробь в виде суммы многочлена и правильной дроби;
– разложить знаменатель дроби на множители;
– разложить правильную дробь на сумму простейших дробей в соответствии с полученными в знаменателе множителями:
множителю
, нужно выделить целую часть, разделив числитель дроби на знаменатель, т.е. представить дробь в виде суммы многочлена и правильной дроби;
– разложить знаменатель дроби на множители;
– разложить правильную дробь на сумму простейших дробей в соответствии с полученными в знаменателе множителями:
множителю  соответствует k дробей
соответствует k дробей 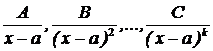 множителю
множителю  соответствует s дробей
соответствует s дробей 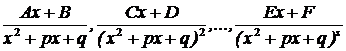 – сумму дробей привести к общему знаменателю;
– приравнять числители дробей;
– приравнять коэффициенты перед одинаковыми степенями х;
– найти неизвестные коэффициенты А, В, С…;
– проинтегрировать получившуюся сумму (получатся интегралы вида I, II, IX).
– сумму дробей привести к общему знаменателю;
– приравнять числители дробей;
– приравнять коэффициенты перед одинаковыми степенями х;
– найти неизвестные коэффициенты А, В, С…;
– проинтегрировать получившуюся сумму (получатся интегралы вида I, II, IX).