Общие сведения
Суждение нередко считают важнейшей формой мышления, поскольку при помощи суждений человек утверждает свое положение в мире. Суждения констатируют существующее положение дел или указывают вектор изменения этого положения.
Суждения представляют собой смысл более сложного знака, чем имя. Иногда слова «суждение» и «высказывание» считают синонимами, однако правильно рассматривать «суждение», как смысл высказывания, как логическую схему повествовательного предложения.
Суждение – это форма мышления, в которой утверждается или отрицается наличие каких-либо ситуаций или связей между ситуациями
Например, все розы имеют шипы. Ни один министр Временного Правительства не был взяточником. Среди студентов нашей группы немало находчивых людей.
Суждения характеризуются логическим значением. Суждение может быть либо истинным, либо ложным. Следует помнить, что понятия не могут быть не истинными, ни ложными, - они могут быть только пустыми. Понятие можно рассматривать как материал для создания суждений.
Аристотель определил истину, как соответствие описания предмета самому предмету. Поэтому истинное суждение устанавливает тождественность мысли и некоторого фрагмента действительности: истинное суждение утверждает некоторую онтологическую связь или отрицает связь несоответствующую действительности (Например, Аристотель - создатель логики. Ни одна лилия не имеет шипов)
Соответственно ложное суждение или утверждает связь, несоответствующую действительности (Гренам – столица Германии) или отрицает некоторую связь, отвечающую состоянию мира (Ни одна рыба не дышит жабрами)
Аристотелевскую логику называют бинарной: в этой логике бытие описывается с помощью сплошных «да» или «нет». Таких значений как «не совсем истинно» эта логика не признает. Чтобы оправдать возможность такого описания действительности необходимо усложнить анализ и ввести понятие «модальность».
|
|
Модальность – это характеристика высказывания по онтологическому статусу и по силе высказываемой мысли.
По онтологическому статусу суждения делятся на атлетические (доступные непосредственной проверке на истину) и деистические, выражающие обязанность, разрешение или запрет (в логике их также называют нормами). Среди атлетических суждений выделяют 2 модальности: модальность возможности (проблематические суждения ◊p) и модальность необходимости (аподиктические суждения □р). Строго говоря, аподиктические суждения имеют место только в математике. В физическом мире господствует модальность возможности. Однако деистические суждения, формирующие право, также носят аподиктический характер (Никого нельзя держать в неволе) Поэтому право называют «математикой свободы». Соотношение между модальностями фиксируются формулами: 
– отрицание р.
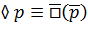
Деистическая модальность содержит сильные характеристики, обязанности (О) и запрет (З) и слабую характеристику – разрешение (Р). Пусть Д - некоторое действие, тогда 
- это действие, исключающее Д.
О (Д) ≡ З 
О (Д) ≡ 
З (Д) ≡ (Д)
З (Д) ≡ О
Р (Д) ≡ 
Р (Д) 
Побудительные предложения сами по себе не относятся к высказываниям, выражающим суждение. Однако их можно преобразовать в суждение деистической модальности ("Стой!" - это побуждение равносильно суждению: "Здесь следует остановиться")
|
|
Вопросительные предложения выражают особую форму мышления - вопрос. Вопрос направлен на уменьшение или устранение познавательной неопределенности. Вопрос предшествует суждению и зачастую ее порождает. Эта связь порой затрудняет оценку истинности суждения: суждение, несвязанное исходным вопросом, субъективно воспринимается как ложное. Исходное знание, содержащееся в вопросе, называют предпосылкой вопроса. Если предпосылка вопроса ложное суждение, то вопрос называют провокационным. В логике неопределенным вопросом называют вопрос, использующий многозначное или неясное понятие. (Справедливо ли передача земли народу?) Тавтологическим вопросом называется вопрос сам в себе содержащий ответ (Между какими странами проходили греко-персидские войны?)
Среди ответов принято выделять сильные и слабые. В первом случае устраняется познавательная неопределенность, а во втором - уменьшается. Тавтологический ответ познавательной неопределенности не уменьшает (Вопрос: с какой скоростью следовало бы ехать, чтобы избежать нарушения? Ответ: со скоростью, обеспечивающую безопасность движения) Нерелевантный ответ - это ответ не на тот вопрос, который задавался. Искусство давать нерелевантные ответы необходимо политикам, а также для сохранения свободы ведущего диалога.
Простые суждения
Простыми суждениями называют суждения, не содержащие более одного утверждения или отрицания. Сложные суждения образуются из простых с помощью логических союзов.
|
|
Принято выделять 3 класса простых суждений:
1) суждения существования (экзистенциальные суждения) - в них констатируется, что нечто имеет место или же нечто подобное отрицается. Например, существует снежный человек (реальность содержит этот объект); в деле отсутствует состав преступления, светает, людей много. Со времен Канта в логике установилось ясное понимание того, что существование не является признаком, а имеет особый статус.
2) суждение с отношениями (реляционные) xRy - запись указывает на то, что смысл лежит в отношении между подлежащим дополнением. Они симметричны, и, поменяв их местами, мы сохраним смысл при верном указании отношения (Псков находится севернее Смоленска, Смоленск располагается южнее Пскова. Сократ - учитель Платона, Платон - ученик Сократа)
3) атрибутивные суждения - суждения этого класса устанавливают связь между объектом и признаком (Все белые медведи - хищники. Некоторые студенты не умеют плавать) Атрибутивные суждения можно рассматривать как включение некоторого множества в другое множество (и тогда суждение будет утвердительным), или же как исключение одного множества из другого (и тогда суждение будет отрицательным)
Для анализа структуры суждения необходимо привести соответствующее высказывание к каноническому виду: следует заменить глагол указанием на некоторое множество объектов и соединить два множества какой-либо связкой (Волга является рекой, впадающей в Каспийской Море) В структуре атрибутивного суждения принято выделять 4 компонента. Первые 2 называют терминами - понятия, входящие в структуру суждения. Логическое подлежащее или понятие о предмете суждения называют субъектом суждения (S). Логическое сказуемое или понятие о признаке, которое приписывается суждению, называют предикатом суждения (Р). Таким образом, смысл высказывания - это его субъектно-предикатная структура (то, о чем говорит, и то, что говорит) Основную смысловую нагрузку суждения несет предикат (Все рыбы (S) дышат жабрами (Р))
В третьем Риме является связка, присутствующая или умалчиваемая глагольная форма, определяющая модальность суждения (атлетическая или деистическая); логический смысл связки - это принадлежность к множеству. В утвердительных суждениях связка приписывает предикат субъекту, а в отрицательных отделяет субъект от предиката (Этот студент не относится к числу отличников). Символическая запись подчеркивает важную роль связки:
S є P (Это утверждение S принадлежит множеству Р) Например, все розы, как некое множество, принадлежат к другому множеству, множеству растений с шипами.
S 
P (Это отрицательное суждение, S не принадлежит Р)
Четвертым элементом выступает количественная характеристика - квантор. Она указывает на степень соотнесенности множества охваченного субъекта с другим множеством, обозначенным предикатом. Если множество S взято в полном объеме, то суждение называют общим. В символической записи:
Если множество S входит во множество носителей P лишь частью объема, то суждение называют частным. В этом случае используют квантор, который читается как "некоторые". Предполагается, что существует хотя бы один элемент S для которого суждение истинно. Суждение будет истинным тогда, когда эти "некоторые" окажутся всем множеством.
В случае регистрирующих понятий любая % доля образует частное суждение. Единичные суждения логика относит не к частным суждениям, а к общим, как их вырожденный случай. (" Сократ смертен", - единичное суждение, которое рассматривается по типу общих; "4 студента не получили зачет по логике",- это единичное суждение, группа из 4-х человек) Атрибутивное суждение с четко обозначенным квантором называют категорическим суждением. Отсутствие квантора в высказывании какого-либо языка порождает двусмысленность, затрудняет понимание ("Все люди агрессивны". Квантор "все" исключения не допускает, также как и квантор "ни один") Говоря о подавляющем большинстве, следует помнить, что речь идет о частном суждении.
Термин "распределенность" в логике имеет специфический смысл. Термин будет распределенным, если он взят в полном объеме (
). Если границы множества остаются вне поля интересов, то термин называют нераспределенным (
, 
)
Объединенная качественно - количественная классификация категорических суждений использует обозначение, взятое из латинских слов, - a ff i rmo n e g o:
1) суждение класса А - общие утвердительные суждения
Например, все люди смертны.
Суждения этого класса можно рассматривать как раскрытие неявных признаков понятия (тот, кто является человеком, тот смертен)
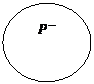
2) суждение класса I - частные утвердительные суждения
Например, некоторые спортсмены - политики.
Единичные понятия не входят в отношение пересечения, поэтому единичные суждения к частным не относятся.
3) суждения класса Е - общие отрицательные суждения
Например, ни один медведь не умеет летать
Суждения подобного позволяют конструировать пустые понятия (Лилия, имеющая шипы; закон, имеющий обратную силу)
4) суждения класса О - частные отрицательные суждения
Например, некоторые студенты не умеют играть на контрабасе
Для любого частного суждения субъектом выступает исходное неразделенное множество.
В итоге возникает сходная таблица распределенности:
| A | I | E | O |
| S | + | - | + | - |
| P | - | - | + | + |
Таблица имеет 2 исключения:
1) суждения класса А, связывающие равнозначные понятия
Все отважные люди - это доблестные люди.
В этом случае предикат суждения А распределен.
2) Среди суждений класса I присутствует суждение с распределенным предикатом. Это выделяющие суждения, в которых признак, обозначенный предикатом, может относиться только к данному субъекту I и не принадлежит никакому другому.
Некоторые люди умеют читать.
 |  | ||||
 | |||||
Сложные суждения
Сложные суждения определяются характером логического союза, который связывает входящие в него компоненты. В логике принято рассматривать 4 основных класса сложных суждений. Для каждого из них характерна своя неповторимая таблица истинности (сочетание логических значений компонентов)
1) соединительные суждения (конъюнкция) - образуются логическим союзом "и" и записывается p^q
Грамматических союзов больше, чем логических. И сложное предложение: "светит солнце, но дует сильный ветер" (на союз "но" логика не обращает внимание)
| p | q | p^q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Конъюнкцию также называют логическим умножением. Она будет истинной при условии истинности всех входящих в нее суждений. Простое суждение со сложным признаком можно рассматривать как конъюнкцию. Это значит, что отрицательное понятие, отрицающее сложный признак, несет сильный компонент неопределенности. Если хороший человек - это добрый и честный человек, то нехороший человек подразумевает 2 возможных варианта.
2) разделительные суждения (дизъюнкция) - образуется логическим союзом "или" («۷»)
Например, подсудимый лжет или недоговаривает.
| p | q | p۷q |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Дизъюнкция будет истинной при наличии хотя бы одного истинного компонента (поэтому ее называют логическим сложением)
Конъюнкция и дизъюнкция связаны между собой законами де Моргана:
В качестве особого подвида дизъюнкции выделяют строгую дизъюнкцию, которая образуется союзом "либо..., либо...". Она обозначается: 
Например, посвящение будет либо 15, либо 16 октября.
3) условное суждение (импликация) - часто называется тяжелой артиллерией логического мышления. Это суждение образуется логическим союзом "если...,то...", и обозначается: p 
q
В логике "р" называют основание, антецедентом, "q" называют следствием, консеквентном.
В структуре юридической нормы антецеденту соответствует гипотеза и диспозиция, а консеквентну - санкция (Если перейдешь дорогу в неположенном месте, то будешь оштрафован)
| p | q | p  q
|
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
Отрицание импликации определяется следующей формулой:
Например, бригадир говорит рабочему: "если будешь продолжать пить, то будешь уволен", бригадир отвечает: "нет, ни за что".
4) эквивалентные суждения - образуются логическим союзом "тогда и только тогда". Их можно рассматривать как симметричную двустороннюю импликацию. Однако принята запись: 
(Обвиняемый подлежит наказанию тогда и только тогда, когда его вина доказана судом)
| p | q | p q
|
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
Очевидно, что различия этого суждения и импликации можно обнаружить в третьей строке. (Сделка действительна при нотариальном оформлении договора. Если возможна импликация, когда договор не оформлен, но сделка действительна, то перед нами импликация. Если это невозможно, то перед нами эквивалент)
Отношение между суждениями
|
|
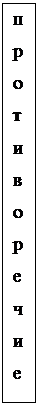Суждения называют сравнимыми, если у них совпадают входящие в них термины. Поэтому суждения "некоторые розы красные" и "некоторые розы темно-красные" не являются сравнимыми, поскольку у них разный предикат. Представления между сравнениями суждений выступает квадрат Пселла, или логический квадрат. Вершины квадрата представляют сравнимые суждения классов А,Е,I,O; а линии в квадрате (стороны и диагонали) представляют отношения между суждениями.
|
|
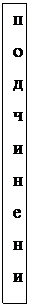
противоположность
| |||
 | |||
 | |||
|
|
|
Схема позволяет выявить 4 вида отношений между суждениями:
1) отношение подчинения
На схеме это отношение выражено боковыми сторонами квадрата. Данное отношение обладает характерной ассиметрией. Из истинности общих суждений следует истинность частных суждений. Однако обратный ход мыслей не верен (как показывает пример)
Ложность частного суждения свидетельствует о ложности общего суждения (Из ложности суждения "некоторые розы фиолетовые" следует ложность суждения "все розы фиолетовые")
Ложность общего суждения оставляет неопределенность в отношении частного суждения. Оно может быть как истинным, так и ложным.
2) отношение противоположности - связывает 2 общих суждения А и Е. Это отношение характеризуется сложной дизъюнкцией.
Это означает несовместимость этих суждений по истинности: если одно из суждений истинно, то второе непременно ложное. Однако ложность одного из суждений не сообщает знания о логическом значении второго суждения. Это отношение можно представить в виде импликации.
3) отношение частичной совместимости (субконтрральность) исключает ситуацию, когда оба суждения ложны (они перекрывают все пространство ложных понятий) Здесь имеет место дизъюнкция по истинности, из которых следуют импликации: 
|
|
 |
4) отношение противоречия изображается обеими диагоналями квадрата, это отношение играет важную роль в логической теории, поскольку однозначно определяет логическое значение второго элемента пары. Эти значения не совместны ни по истинности, ни по ложности.
Отношение противоречия играет важную роль при определении операции отрицания суждения. В ходе этой операции осуществляется переход к суждению, имеющее другое качество и другой квантор (получается суждение, противоречащее исходному)
Здесь возможны 2 ошибки:
1)отрицание сводится к изменению квантора (не все розы прекрасны)
2)отрицание сводится исключительно к изменению качества (суждение "все преступники аморальны" отрицается заведомо ложным суждением "ни один преступник не является аморальным")
Поэтому, квадрат в целом представляет собой верный диагональный ход мыслей. Общее утвердительное суждение отрицается не общим отрицанием, а частным, т.е. указывается хотя бы один объект (Суждение "все албанцы террористы", опровергается суждением класса "О" - "некоторые албанцы не являются террористами" (мать Тереза))
Отношения между простыми суждениями моделируют отношения между сложными. Среди них также можно выделить отношение противоположности и частичной совместимости. В первом случае возможно, что оба суждения ложны, но исключается их обоюдная истинность.
Например:
1) Убийство осуществлено подсудимым и совершилось ночью
2) Убийство было совершено подсудимым и было совершено в светлое время суток
p˄q
p˄
Отношение частичной совместимости напротив исключает ситуацию ложности обоих суждений. Здесь возможна совместимость по истинности.
Например, показания 2-х свидетелей:
1) на подозреваемой была то ли черная юбка, то ли черная кофта
2) исключено, что подозреваемая была вся в черном
p˅q
Отношение противоречия задается правилами отрицания суждения в этом случае (частности и законы Д. Моргана):