Подготовка к сдаче экзамена по математике, 2 семестр (август, комиссия)
Структура билета
1. Теоретический вопрос по теме № 1.
2. Теоретический вопрос по теме № 2.
3. Практика по теме «Функции одной переменной: пределы, непрерывность»
4. Практика по теме «Дифференцирование функции одной переменной»
5. Практика по теме «Функции многих переменных»
Список теоретических вопросов по теме № 1
- Понятие функции, основные характеристики функции (область определения, область значений, график функции, четность, монотонность, периодичность, ограниченность). Способы задания функции.
- Основные элементарные функции. Обзор функций


 .
. - Основные элементарные функции. Обзор функций


 ,
,  .
. - Основные элементарные функции. Обзор функций
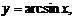
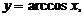
 ,
,  .
. - Предел числовой последовательности. Примеры сходящихся и расходящихся последовательностей. Свойства предела числовой последовательности.
- Бесконечно малые и бесконечно большие числовые последовательности и их свойства. Примеры.
- Предел функции в точке. Свойства предела функции. Примеры.
- Непрерывность функции в точке. Классификация точек разрыва. Примеры.
- Понятие производной функции, её геометрический смысл. Примеры. Таблица производных основных элементарных функций.
- Понятие производной функции, её геометрический смысл. Примеры. Правила дифференцирования.
- Дифференциал функции, его геометрический смысл. Примеры. Применение дифференциала в приближенных вычислениях.
- Правила Лопиталя. Различные виды неопределенностей при вычислении пределов. Примеры.
- Точки экстремума функции одной переменной. Необходимые и достаточные условия существования точек экстремума. Примеры.
- Возрастание и убывание функции
 на интервале. Необходимое и достаточное условия возрастания (убывания) функции на интервале. Примеры.
на интервале. Необходимое и достаточное условия возрастания (убывания) функции на интервале. Примеры. - Выпуклость графика функции
 на интервале. Точки перегиба. Необходимое и достаточное условие выпуклости вверх (вниз) функции на интервале, существования точек перегиба. Примеры.
на интервале. Точки перегиба. Необходимое и достаточное условие выпуклости вверх (вниз) функции на интервале, существования точек перегиба. Примеры. - Асимптоты графика функции
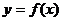 . Вертикальные и наклонные асимптоты и способы их нахождения. Примеры.
. Вертикальные и наклонные асимптоты и способы их нахождения. Примеры.
Список теоретических вопросов по теме № 2
- Понятие функции многих переменных. Примеры. График функции 2-х переменных. Линии уровня (кривые безразличия). Предел функции 2-х переменных в точке. Непрерывность функции 2-х переменных в точке.
- Частные и полные приращения функции
 в точке. Частные производные функции
в точке. Частные производные функции  в точке, их геометрический смысл. Примеры.
в точке, их геометрический смысл. Примеры. - Дифференцируемость функции
 в точке и ее связь с непрерывностью. Примеры.
в точке и ее связь с непрерывностью. Примеры. - Полное приращение и полный дифференциал функции
 в точке, их геометрические смыслы. Применение полного дифференциала в приближенных вычислениях. Примеры.
в точке, их геометрические смыслы. Применение полного дифференциала в приближенных вычислениях. Примеры. - Касательная плоскость и нормаль к поверхности, заданной как явно, так и неявно. Примеры.
- Частные производные высших порядков функции
 . Теорема о смешанных производных одного порядка. Примеры.
. Теорема о смешанных производных одного порядка. Примеры. - Градиент функции многих переменных. Свойства градиента. Примеры.
- Производная по направлению. Способы её вычисления. Связь производной по направлению с градиентом. Примеры.
- Экстремумы функции
 . Необходимые условия существования экстремума дифференцируемой функции. Примеры.
. Необходимые условия существования экстремума дифференцируемой функции. Примеры. - Экстремумы функции
 . Достаточные условия существования экстремума дифференцируемой функции. Примеры.
. Достаточные условия существования экстремума дифференцируемой функции. Примеры.
Практика по теме «Функции одной переменной: пределы, непрерывность» (примерные задачи):
- Исследовать функцию на непрерывность. Указать точки разрыва и их род, если они имеются:
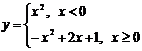 .
. - Исследовать функцию на непрерывность. Указать точки разрыва и их род, если они имеются:
 .
. - Используя только график функции указать её точки разрыва и определить их род
 .
. - Вычислить предел
 .
. - Вычислить предел
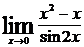 .
. - Вычислить предел
 .
. - Найти вертикальные асимптоты графика функции
 .
. - Найти наклонные асимптоты графика функции
 .
. - Найти односторонние пределы функции
 в точке
в точке  и выяснить характер разрыва в этой точке.
и выяснить характер разрыва в этой точке. - Найти односторонние пределы функции
 в точке
в точке  и выяснить характер разрыва в этой точке.
и выяснить характер разрыва в этой точке.
Практика по теме «Дифференцирование функции одной переменной» (примерные задачи):
- Найти дифференциал функции
 в точке
в точке 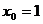 , если
, если  .
. - Найти уравнение касательной к графику функции
 в точке
в точке  .
. - Составить уравнение нормали к графику функции
 в точке
в точке  .
. - Найти точки экстремума функции
 .
. - Найти точки перегиба графика функции
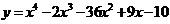 .
. - Найти
 , если функция
, если функция  задана параметрически
задана параметрически  .
. - Вычислить приближенно значение числового выражения
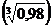 .
. - Построить схематично график функции
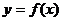 в окрестности точки М(1;-2), если известно что
в окрестности точки М(1;-2), если известно что  ,
,  .
. - Найти наибольшее и наименьшее значение функции
 на отрезке [-1;1].
на отрезке [-1;1]. - Какой эскиз соответствует поведению функции y(x) в окрестности точки М, y’(M)=0, y’’(M)>0?
1)  2)
2)  3)
3)  4)
4) 
5)  6)
6)  7)
7)  8)
8) 
Практика по теме «Функции многих переменных» (примерные задачи):
- Найти и построить семейство линий уровня функции
 .
. - Найти производную функции
 в точке
в точке  в направлении наибыстрейшего роста функции.
в направлении наибыстрейшего роста функции. - Найти производную функции
 в точке
в точке  в направлении вектора
в направлении вектора  .
. - Найти производную функции
 в точке
в точке  в направлении, составляющим с осью Ох угол в
в направлении, составляющим с осью Ох угол в  .
. - Составить уравнение касательной плоскости к поверхности, заданной уравнением
 в точке М(1;1;3).
в точке М(1;1;3). - Найти точки экстремума функции
 .
. - Найти
 в точке
в точке  , если
, если  ,
,  ,
,  .
. - Найти
 в точке
в точке  , если
, если  ,
,  ,
, 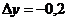 .
. - Найти
 , если
, если  ,
,  .
. - Составить уравнение нормали к поверхности, заданной уравнением
 в точке
в точке  .
. - Найти
 , если
, если  ,
,  .
. - Найти
 , если
, если  ,
,  ,
,  ,
, 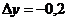 .
.