Балтийский Государственный Технический Университет «Военмех» им. Д.Ф.Устинова
Кафедра Н1
Домашняя работа по дисциплине:
«Применение мехатронных систем» на тему:
«Управление объектом с упругими свойствами»
| Выполнил: студент гр. Н192 Купцов А.А. Принял: Юсупов А.Н. |
Санкт-Петербург
Описание системы управления
Объект управления
В данной работе приведено исследование системы управления автоматических одностворчатых раздвижных дверей. Схема системы представлена на рисунке 1.
На схеме также обозначены:
x – координата (положение) створки,
m – масса створки
FT – тяга привода.
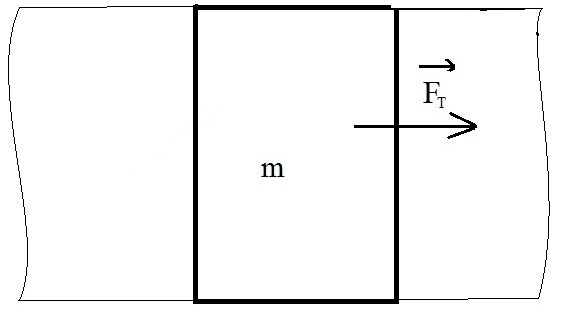
Рисунок 1. Автоматические одностворчатые раздвижные двери
Параметры системы:
1) Масса створки двери m=50 кг.
2) Максимальная поступательная скорость створки v=2,5 м/с.
3) Коэффициент сухого трения: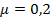 
.
4) Время квантования системы: Т=0,01 с
Функциональная схема системы управления.
Функциональная схема исследуемой системы управления показана на рисунке 2. Задающий сигнал положения xg, и сигналы с измерительного устройства ИУ (текущее положение створки двери x и скорость створки двери dx/dt) поступают на регулятор положения Р, который на основании этих сигналов выдает управляющий сигнал u. Управляющий сигнал поступает на привод П, который прикладывает заданное усилие FT на объект управления О.
| x |
| FT |
| u |
| Р |
| П |
| О |
| ИУ |
| xg |
| dt |
| dx |
| x, |
| Рисунок 2. Функциональная схема |
Математическая модель объекта управления.
При разработке упрощенной математической модели были приняты следующие особенности работы привода:
– привод автоматических является идеальным и максимально быстро отрабатывает заданную скорость, что позволяет пренебречь переходными процессами в приводе;
– привод является реверсивным и независимо от скорости перемещения автоматических дверей может обеспечить заданную скорость движения двери в заданных пределах.
– движение происходит в горизонтальной плоскости;
– динамика автоматических дверей рассматривается как движение материальной точки.
Математическая модель объекта:
Заданный объект управления описывается следующим уравнением второго порядка
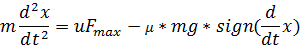
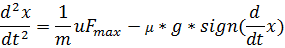
m-масса створок дверей.
u-сигнал управления
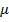- коэффициент сухого трения.
Fmax – максимальная тяга привода.
sign – функция получения знака от его аргумента, в данном случае от скорости объекта.
Схема реального объекта управления:
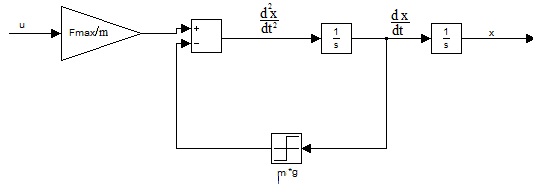
Рисунок 3. Схема реального объекта управления.
Рассчитываем идеальный объект управления:
К0=Fmax – Коэффициент идеального источника.
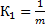- Коэффициент идеального накопителя
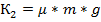- Коэффициент потерь
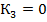-Коэффициент реакции внешней среды
Схема обобщенного объекта управления:
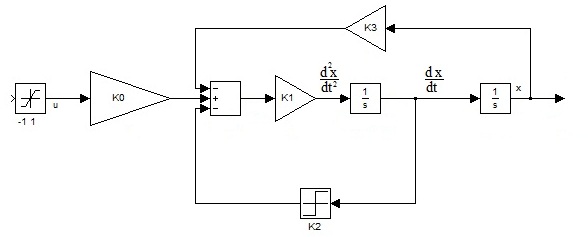
Рисунок 4. Схема обобщенного объекта управления
Схема идеального объекта управления(без учета реакции внешней среды и потерь на трение):
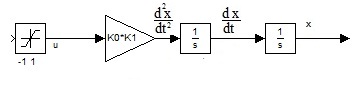
Рисунок 5. Схема идеального объекта управления.
Разработка дискретной системы управления идеальным объектом
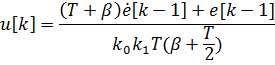
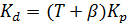
Параметры регулятора считаются с помощью скрипта, текст которого приведен в приложении 1. Коэффициент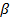 
определяет быстродействие системы. В данном случае он был подобран как β=T*23 исходя из требования обеспечения максимального быстродействия без перерегулирования. Параметры регулятора: Kd=17,0213;Kp=70,922;