Содержание
Содержание……………………………………………………………..………..……..……..2
Цель работы……………………………………………………………............……….……..3
Задания на расчетно-графическую работу 2.1.1 – 2.1.10..………….………….……….3-16
Вывод…………………………………………………………………………….………..…17
Список использованной литературы……………...………………………….……………18
Цель работы
Изучение расширенных возможностей табличного процессора MS Excel и их использование при решении вычислительных задач. Научиться решать финансовые, экономические, математические и статические задачи. С помощью электронной таблицы решать задачи, таких как обработка заказов и планирование производства, расчет налогов и заработной платы, учет кадров и издержек, управление сбытом, составление прайс-листов и др. Правильно использовать функции из категории инженерные, математические, ссылки, массивы и др. Научиться строить графики, выполнять по различным критериям автофильтрацию, определить некоторые основные характеристики потоков различных жидкостей, решать систему уравнении методом Крамера и методом обратной матрицы.
Задания на расчетно-графическую работу
2.1.1. Используя методику перевода чисел (таблица В.1), а также ресурсы MS Excel:
- создать таблицу перевода заданного числа (таблица Б.1) из десятичной системы счисления в предлагаемую систему счисления (двоичную, восьмеричную, шестнадцатеричную);
- создать таблицу обратного перевода полученного результата в десятичную систему. Выполнить те же действия, используя встроенную функцию из категории Инженерные (подключить Пакет анализов). Объяснить возможные ошибки;
- с помощью специальной функции из категории Математические перевести заданное число (таблица Б.1) из десятичной системы счисления в римскую систему счисления и получить тот же результат.
Пояснение: было задано число в десятичной системе, мне нужно было перевести это число в восьмеричную систему, для этого я сначала делил заданное число в десятичной системе на основание системы, до тех пор пока не получил число меньше основания системы, при этом сразу использовал функцию ЦЕЛОЕ, после этого с помощью функции ОСТАТ я получил остатки деления, затем с помощью функции СЦЕПИТЬ объединил результат.
| Перевести из десятичной системы в шестнадцатеричную систему счисления | |
| Число в десятичной системе | |
| Основание системы |
| перевод из десятичной в восьмеричную | |
| число в десятичной системе | |
| число в восьмеричной системе |
| Частное | Остаток | Целое |
| Число в шестнадцатеричной системе |
| перевод из восьмеричной в десятичную | |
| число в восьмеричной системе | |
| число в десятичной системе |
Пояснение: с помощью функции ВОС.В.ДЕС я перевёл число из восьмеричной системы обратно в десятичную систему.
Пояснение: заданное число в десятичной системе я переёл в римскую систему исчисления, с помощью функции РИМСКОЕ, и сделал обратное действие, перевёл из римской системы счисления в десятичную.
| Перевести из десятичной в римскую систему счисления | |
| Число | |
| Результат | MMDCLXXXIX |
| Обратный перевод из римской системы счисления в десятичную | |
| M | |
| M | |
| D | |
| C | |
| L | |
| X | |
| X | |
| X | |
| I | -1 |
| X | |
| I |
Пояснение: над заданными числами a и b я совершил заданную мне арифметическую операцию, число а умножил на число b.
| Арифметическая операция над заданными числами | |
| a | |
| b | |
| а*b |
2.1.2. Используя функцию преобразования из категории Инженерные, составить таблицу перевода данных из одних единиц измерения (таблица Б.1) в другие.
| Исходные данные | |
| H | |
| Единица результата | |
| Дина |
Пояснение: для того чтобы перевести Градус Цельсия в Кельвин я использовал функцию ПРЕОБР (число – заданное число, исходная единица измерения – “С”, конечная единица измерения – “K”).
2.1.3. Построить график функции (таблица Б.3).
Пояснение: для того чтобы построить график функции сначала я построил таблицу, значение t я взял произвольное (30), затем значения t перевел в радианы r. Затем полученные значения r подставил в заданные функции, получил значения х и y (пример: =10*(COS(C9)^3)), после всего этого я построил диаграмму, подставив в диапазон данных столбцы со значениями x и y, для построения графика выбрал тип диаграммы Точечная.
| Построить график функции | t начальное | шаг | ||
| Функция | a=(1+cos(v))\r | b=(1+sin(v))\r |
| v | r | a | b |
| 0,436332 | 4,563500691 | 1,988503313 | |
| 0,523599 | 2,204457886 | 0,022857914 | |
| 0,610865 | 0,157658005 | 0,936077705 | |
| 0,698132 | 0,477076085 | 2,499690472 | |
| 0,785398 | 1,942100275 | 2,356643561 | |
| 0,872665 | 2,251685206 | 0,845256155 | |
| 0,959931 | 1,064791805 | 0,000255046 | |
| 1,047198 | 0,045442256 | 0,663856956 | |
| 1,134464 | 0,385685349 | 1,610301127 | |
| 1,22173 | 1,336889956 | 1,451949277 | |
| 1,308997 | 1,468109827 | 0,467700379 | |
| 1,396263 | 0,637138204 | 0,004376929 | |
| 1,48353 | 0,010531205 | 0,555381054 | |
| 1,570796 | 0,351367249 | 1,205755725 | |
| 1,658063 | 1,043490978 | 1,015197811 | |
| 1,745329 | 1,067030115 | 0,282831654 | |
| 1,832596 | 0,414188981 | 0,016078132 | |
| 1,919862 | 0,00051003 | 0,497826007 | |
| 2,007129 | 0,33589785 | 0,969262904 | |
| 2,094395 | 0,866207607 | 0,754686249 | |
| 2,181662 | 0,819427972 | 0,17599409 | |
| 2,268928 | 0,278857973 | 0,030804877 | |
| 2,356194 | 0,001660374 | 0,461918017 | |
| 2,443461 | 0,328299261 | 0,810424107 | |
| 2,530727 | 0,744396003 | 0,579969677 | |
| 2,617994 | 0,649065997 | 0,108909181 | |
| 2,70526 | 0,189570905 | 0,04683025 | |
| 2,792527 | 0,00872711 | 0,436674505 | |
| 2,879793 | 0,324211837 | 0,693729409 | |
| 2,96706 | 0,653170118 | 0,453866649 | |
| 3,054326 | 0,523350854 | 0,065109419 | |
| 3,141593 | 0,12781413 | 0,063295082 | |
| 3,228859 | 0,019200218 | 0,417057893 | |
| 3,316126 | 0,321552014 | 0,602449826 | |
| 3,403392 | 0,580486372 | 0,358305671 | |
| 3,490659 | 0,426047886 | 0,036297651 | |
| 3,577925 | 0,084062899 | 0,079683754 | |
| 3,665191 | 0,031682527 | 0,400447984 | |
| 3,752458 | 0,319199858 | 0,527719612 | |
| 3,839724 | 0,519851163 | 0,283457512 | |
| 3,926991 | 0,348185018 | 0,017801193 | |
| 4,014257 | 0,052887507 | 0,095643047 | |
| 4,101524 | 0,04530061 | 0,385365718 | |
| 4,18879 | 0,316506972 | 0,464440819 | |
| 4,276057 | 0,467491968 | 0,22352076 | |
| 4,363323 | 0,284413569 | 0,00675448 | |
| 4,45059 | 0,03093891 | 0,110908534 | |
| 4,537856 | 0,059456677 | 0,370932811 | |
| 4,625123 | 0,313082878 | 0,409504865 | |
| 4,712389 | 0,421098929 | 0,174848481 |
Диаграмма

2.1.4. Имеется резервуар с емкостью V, рабочим объемом Vr, объем жидкости в резервуаре Vg. Резервуар в основании имеет круг радиусом r или прямоугольник со сторонами a и b и высоту заполнения h (таблица Б.4). Как только объем жидкости станет превышать рабочий объем резервуара, оператору необходимо отправить сообщение, используя логическую функцию ЕСЛИ. Сообщение “перекрыть клапан” должно быть написано на красном фоне, в противном случае, должно быть выведено сообщение – “не требуется”. Используя условное форматирование, проиллюстрировать заполнение резервуара.
Пояснение: вначале я нашёл площадь основания S(П*r^2), затем после этого записал формулу для нахождения объёма жидкости (=G8*E8), потом с помощью функции ЕСЛИ отправил нужное сообщение (=ЕСЛИ(F8>D8;"перекрыть клапан";"не требуется")), затем построил диаграмму использовав условное форматирование, и сообщение «перекрыть клапан» сделал на красном фоне.
| Основание резервуара | Рабочий объём Vr | Площадь основания S | Объем жидкости V | Высота заполнения h | |
| a | b | ||||
| 5,5 | 38,5 | 115,5 |
| перекрыть клапан | ||
| раб.оъем Vr | ||
2.1.5. Решить систему уравнений (таблица Б.5) методом обратной матрицы и методом Крамера.
Решить систему уравнений методом обратной матрицы
| 2x1-x2+2x3=0 | |
| Дано | 4x1+x2+4x3=0 |
| x1+x2+2x3=4 |
Пояснение: сначала записал уравнение в матричной форме, затем с помощью функции МОПРЕД нашёл определитель матрицы, после этого с помощью функции МОБР нашёл обратную матрицу, потом нашёл значения матрицы X, для этого умножил обратную матрицу на правую часть уравнения или матрицу С, с помощью функции МУМНОЖ.
| Матрица A | -1 | |||
| Матрица X | x1 |
| x2 | |
| x3 |
| Матрица C | |
| Определитель матрицы A |
| Обратная матрица | 0,16953 | 0,103194103 | 0,012285012 | |||
| -0,3219 | 0,412776413 | 0,049140049 | ||||
| 0,02703 | -0,02702702 | -0,027027027 | ||||
| х1 | -4 | |||||
| х2 | ||||||
| х3 | ||||||
Решить систему уравнений методом Крамера
Пояснение: нашёл вспомогательные определители матриц 1, 2, 3 с помощью функции МОПРЕД, после этого для того чтобы найти x1, x2, x3 разделил соответствующее определители на определитель матрицы А, и получил нужные мне значения.
| Матрица1 | -6 | -1 | |
| -14 | |||
| -16 | -3 | -42 | |
| Матрица2 | -6 | ||
| -14 | |||
| -16 | -42 | ||
| Матрица3 | -1 | -6 | |
| -14 | |||
| -3 | -16 |
| Определитель матрицы 1 | -24 |
| Определитель матрицы 2 | |
| Определитель матрицы 3 |
| х1 | -4 |
| х2 | |
| х3 |
2.1.6. Используя функцию MS Excel, выполнить с заданным массивом (таблица Б.6) следующие действия:
- транспонировать исходный и транспонированный массивы;
- перемножить исходный и транспонированный массивы;
- найти позицию элемента равного заданному числу А.
Пояснение: заданный массив я транспонировал с помощью функции ТРАНСП, и получил матрицу В, затем перемножил матрицу В на её транспонированную матрицу с помощью функции МУМНОЖ и получил результат, после этого с помощью функции ПОИСКПОЗ нашёл позицию числа А.
| Исходная матрица | -4 | ||||
| A | -4 |

Транспонировать исходную матрицу
| Транспонированная матрица | |||||||
| -4 | |||||||
Перемножить исходную матрицу и транспонированную матрицу
| Результат | -4 | ||||
| -4 | |||||
| Найти позицию элемента равного заданному числу A | |||||
| Столбец | |||||
| Строка |
2.1.7. Определить некоторые основные характеристики потоков различных жидкостей:
а) вода течет по трубе с внутренним диаметром D (таблица Б.7). Средняя скорость потока равна v. Вычислить площадь сечения трубы S= (π/4)*D² и объемную скорость потока V= v*S. Определить какого диаметра должна быть труба, чтобы скорость потока жидкости снизилась до 1,3 м/с при неизменной объемной потока;
б) на практике широко применяется правило: средняя скорость легкоподвижных жидкостей (вязкость которых по порядку величины совпадает с вязкостью воды) в трубе не должна превышать 1м/с. Определите минимальный диаметр трубы, по которой должно поступать 6000м³ воды в день при соблюдений сформулированного правила;
в) число Рейнольдса определяется соотношением Re = D*v*ρ/μ, где D – внутренний диаметр трубы, ν – средняя скорость потока жидкостей в трубе, ρ - плотность жидкости, μ - абсолютная вязкость жидкости. Если для потока жидкости в трубе величина числа Рейнольдса не превышает 2100, поток считается ламинарным. Если же его величина превышает 10000, поток считается турбулентным. Для значений, лежащих в диапазоне от 2100 до 10000, невозможно заранее определить тип потока. Найти число Рейнольдса и определить тип потока (ламинарный, турбулентный или неизвестный) для жидкостей, характеристики которых указаны в таблице Б.7.
Вычислить площадь поперечного сечения трубы и объёмную скорость потока
Пояснение: по исходным мне данным и формулам, вначале я вычислил площадь поперечного сечения (=ПРЕОБР(B10;"mm";"m")^2*ПИ()/4), затем нашёл объёмную скорость потока (=D10*E10), потом площадь поперечного сечения (=B19/C19) и диаметр трубы (=ПРЕОБР((4*D19/ПИ())^0,5;"m";"mm")) при скорости 1,3 м/с, затем определил площадь поперечного сечения (=(C28/ПРЕОБР(1;"day";"sec"))/1) и диаметр трубы (=ПРЕОБР((4*D28/ПИ())^0,5;"m";"mm")) при средней скорости потока 1 м/с и объёмной скорости потока 6000 м^3/день, затем определил число Рейнольдса (=C37*D37*ПРЕОБР(B37;"mm";"m")/E37) по исходным данным, и с помощью функции ЕСЛИ указал тип потока (=ЕСЛИ(F37<2100;"ламинарный"; ЕСЛИ(F37>10000;"турбулентный"; «неизвестный")).
| S=π*D^2/4 | V=v*S |
| Диаметр трубы D, мм | Вид жидкости | Средняя скорость потока v, м/с | Площадь поперечного сечения S, м^2 | Объёмная скорость потока V, м^3/с | |
| 980,6 | нефть | 1,5 | 0,755220307 | 1,132830461 |
Определить диаметр трубы при средней скорости потока жидкости 1,3 м/с, и неизменной объёмной скорости
| S=V/v | D=(4*S/π)^0,5 |
| Объёмная скорость потока V, м^3/с | Средняя скорость потока v, м/с | Площадь поперечного сечения S, м^2 | Диаметр трубы D, мм | |
| 1,132830461 | 1,5 | 0,755220307 | 980,6 |
Определить минимальный диаметр трубы при средней скорости потока жидкости не превышающей 1 м/с
| S=V/v | D=(4*S/π)^0,5 |
| Средняя скорость потока v, м/с | Объём скорость потока V, м^3/день | Площадь поперечного сечения S, м^2 | Диаметр трубы D, мм | |
| 25691387,27 |
Найти число Рейнольдса и определить тип потока
Re=D*v*ρ/μ
| Диаметр трубы D, мм | Средняя скорость потока v, м/с | Плотность жидкости ρ, кг/м^3 | Абсолютная вязкость жидкости μ, 10^-4*Па*с | Число Рейнольдса Re | Тип потока | |
| 980,6 | 1,5 | 2,8 | 457,0296429 | ламинарный |
2.1.8. Резисторный датчик температуры – это прибор, в котором для изменения температуры используется металлическая проволока или пластинка. Электрическое сопротивление металла зависит от температуры, поэтому температуры можно вычислить на основе измерений сопротивления металла. Уравнение, связывающее температуру и сопротивление, имеет вид:
Rt = R0(1+άT)
где Rt – сопротивление при изменяемой температуре Т;
R0 – сопротивление при температуре 0ºС;
ά – линейный температурный коэффициент.
Для платины ά = 0,00385 Ом/ ºС. Вычислить (таблица Б.8)
а) сопротивление платинового терморезистора в заданном интервале температур (Т 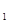 ;Т
;Т  ) с указанным шагом h
) с указанным шагом h  при известном сопротивлении R
при известном сопротивлении R  ;
;
б) температуру, при которой сопротивление терморезистора равно заданным значениям R  c указанным шагом h
c указанным шагом h  .
.
Вычислить сопротивление платинового терморезистора в интервале температур (T1; T2)
Rt=R0*(1+αT)
Пояснение: по исходным данным и формуле я определил сопротивления на данном промежутке температур (пример: =$B$11*(1+$C$11*G11) и т.д.), затем наоборот по данным сопротивлениям определил температуры (пример: =((G38-$B$38)/$B$38)/$C$38 и т.д.).
| Сопротивление при температуре 0°С, R0 | Линейный температурный коэффициент, α | Шаг температур, Ht | Нижняя температура, T1 | Верхняя температура, T2 | |
| 0,00385 |
| Температуры, T | Сопротивление при измеряемой температуре T, Rt | |
| 69,25 | ||
| 71,175 | ||
| 73,1 | ||
| 75,025 | ||
| 76,95 | ||
| 78,875 | ||
| 80,8 | ||
| 82,725 | ||
| 84,65 | ||
| 86,575 | ||
| 88,5 | ||
| 90,425 | ||
| 92,35 | ||
| 94,275 | ||
| 96,2 | ||
| 98,125 | ||
| 100,05 | ||
| 101,975 | ||
| 103,9 |
Вычислить температуру при которой сопротивление терморезистора равно заданным значениям R(t1;t2)
t=((Rt-R0)/R0)/α
| Сопротивление при температуре 0°С, R0 | Линейный температурный коэффициент, α | Шаг температур, Hr | Сопротивление при температуре t1, Rt1 | Сопротивление при температуре t2, Rt2 | |
| 0,00385 |
| Сопротивление терморезистора, Rt | Температуры, t | |
| 259,7402597 | ||
| 285,7142857 | ||
| 311,6883117 | ||
| 337,6623377 | ||
| 363,6363636 | ||
| 389,6103896 | ||
| 415,5844156 | ||
| 441,5584416 | ||
| 467,5324675 | ||
| 493,5064935 | ||
| 519,4805195 |
2.1.9. Сформировать предложенную таблицу, заполнить не менее 10 записей и выполнить выборку данных по различным критериям (три простых запроса с помощью автофильтрации и три сложных запроса с использованием расширенного фильтра).
Пояснение: я сформировал таблицу из 10 записей “соревнования”, затем сделал три запроса с помощью автофильтрации, и три запроса с использованием расширенного фильтра.
Исходная таблица
| ФИО абонента | Телефон | Год установки | Статус абонента | Плата за телефон |
| Ахметов Ильяс Вагизулы | 258-22-02 | Подключен | ||
| Айманбеков Дулат Кадырович | 258-36-06 | Временно отключен | ||
| Банников Алексей Юрьевич | 247-02-31 | Подключен | ||
| Ван Петр Игоревич | 236-97-65 | Недоступен | ||
| Итрина Илона Ивановна | 234-87-09 | Подключен | ||
| Кауметов Мурат Сапаевич | 265-98-05 | Подключен | ||
| Краузе Андрей Романович | 227-98-67 | Временно отключен | ||
| Ким Марина Аликовна | 234-87-09 | Подключен | ||
| Леонова Инна Михайловна | 234-98-45 | Подключен | ||
| Яшина Антонина Викторовна | 245-98-56 | Подключен |
Запрос с помощью автофильтра и с использованием расширенного фильтра
| ФИО абонента | Телефон | Год установки | Статус абонента | Плата за телефон |
| Кауметов Мурат Сапаевич | 265-98-05 | Подключен | ||
| Ван Петр Игоревич | 236-97-65 | Недоступен | ||
| Итрина Илона Ивановна | 234-87-09 | Подключен | ||
| Ким Марина Аликовна | 234-87-09 | Подключен | ||
| Леонова Инна Михайловна | 234-98-45 | Подключен | ||
| Яшина Антонина Викторовна | 245-98-56 | Подключен |
Диапазон условий 1
| ФИО абонента | Телефон | Год установки | Статус абонента | Плата за телефон |
| Кауметов Мурат Сапаевич | 265-98-05 | Подключен |
Результат
| ФИО абонента | Телефон | Год установки | Статус абонента | Плата за телефон |
| Ахметов Ильяс Вагизулы | 258-22-02 | Подключен | ||
| Итрина Илона Ивановна | 234-87-09 | Подключен |
Диапазон условий 2
| ФИО абонента | Телефон | Год установки | Статус абонента | Плата за телефон |
| Яшина Антонина Викторовна | 245-98-56 | Подключен |
Результат
| ФИО абонента | Телефон | Год установки | Статус абонента | Плата за телефон |
| Айманбеков Дулат Кадырович | 258-36-06 | Временно отключен | ||
| Краузе Андрей Романович | 227-98-67 | Временно отключен |
Результат
| ФИО абонента | Телефон | Год установки | Статус абонента | Плата за телефон |
| Ахметов Ильяс Вагизулы | 258-22-02 | Подключен | ||
| Банников Алексей Юрьевич | 247-02-31 | Подключен | ||
| Итрина Илона Ивановна | 234-87-09 | Подключен | ||
| Кауметов Мурат Сапаевич | 265-98-05 | Подключен | ||
| Ким Марина Аликовна | 234-87-09 | Подключен | ||
| Леонова Инна Михайловна | 234-98-45 | Подключен | ||
| Яшина Антонина Викторовна | 245-98-56 | Подключен |
2.1.10. Сформировать заданные основную и вспомогательную таблицы. Выполнить в основной таблице все необходимые вычисления, используя данные вспомогательной таблицы.
Пояснение: я сформировал основную и вспомогательную таблицы, для связи таблиц я использовал функцию ВПР, затем нашел, сколько всего выделено.
Основная таблица
| наименование металла | Количество э/энергии на переработку 1 т металла | кол-во металла (т) | Расход э/энергии | Стоимость тг | |
| Медь черновая | |||||
| Титан | |||||
| Цинк | |||||
| Магний | |||||
| Цинк | |||||
| Титан | |||||
| Медь черновая | |||||
| Магний | |||||
| Цинк | |||||
| Итого |
Вспомогательная таблица
| наименование металла | Количество э/энергии на переработку 1 т металла |
| Цинк | |
| Титан | |
| Магний | |
| Медь черновая |
Вывод
По окончании проделанной работы я изучил расширенные возможности табличного процессора MS Excel. Научился использовать их при решении различных задач, например: работать в различных системах счисления; оперировать с переводом из одной системы единиц измерения в другую; строить графики и диаграммы различных типов; также на примере матриц я освоил всевозможные арифметические операции; научился правильно применять и использовать функции из категории инженерные, математические, ссылки, массивы и др.; на практике обучился построению графиков функций, выполнению автофильтрации в зависимости от требуемых критериев, определению некоторых основных характеристик потоков различных жидкостей; научился решать системы уравнений различными методами и т.д.
Список использованной литературы
1. Сябина Н.В., Ешпанова М.Д., Аманбаев А.А. Информатика. Методические указания к расчетно-графическим работам для студентов всех специальностей всех форм обучения. – Алматы: АИЭС, 2008.
2. Безручко В.Т. Практикум по курсу «Информатика». Работа в Windows, Word, Excel. – М.: Финансы и статистика, 2003.
3. Информатика. Базовый курс. Учебное пособие под редакцией Симоновича С.В. – СПб: Питер 2003.
4. Бондаренко С. Microsoft Office 2003 в теории и практике. – М.: ООО Новое знание, 2004.
5. Акулов О.А., Медведев Н.В. Информатика: базовый курс. – М.: Омега-Л, 2009.