Задание номер 186. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=143/X=1.19} равна
0,375
Задание номер 187. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=188/X=1.59} равна
0,25
Задание номер 188. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=86/X=1.1} равна
1/6
Задание номер 189. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=57/X=1.8} равна
0,5
Задание номер 190. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=145/X=0.42} равна
0,5
Задание номер 191. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=105/X=1.19} равна
0,5
Задание номер 192. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=135/X=1.26} равна
11/46
Задание номер 193. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=80/X=0.88} равна
1/3
Задание номер 194. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=149/X=1.56} равна
7/33
Задание номер 195. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=147/X=1.59} равна
0,55
Задание номер 196. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=178/X=0.83} равна
11/29
Задание номер 197. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=226/X=1.19} равна
7/19
Задание номер 198. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=224/X=1.67} равна
|
|
0,25
Задание номер 199. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=150/X=1.19} равна
11/32
Задание номер 200. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{Y=173/X=1.30} равна
8/33
Задание номер 201. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.36/Y=43} равна
0,25
Задание номер 202. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.46/Y=88} равна
9/19
Задание номер 203. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.52/Y=151} равна
9/22
Задание номер 204. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.85/Y=99} равна
11/37
Задание номер 205. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.79/Y=109} равна
1/34
Задание номер 206. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.40/Y=180} равна
7/19
Задание номер 207. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=0.76/Y=155} равна
1/46
Задание номер 208. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.59/Y=119} равна
11/39
Задание номер 209. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.60/Y=96} равна
|
|
14/39
Задание номер 210. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=0.25/Y=45} равна
1/3
Задание номер 211. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.3/Y=77} равна
0,36
Задание номер 212. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.74/Y=106} равна
11/18
Задание номер 213. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=0.87/Y=100} равна
7/34
Задание номер 214. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.49/Y=159} равна
11/35
Задание номер 215. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.59/Y=162} равна 
7/19
Задание номер 216. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=0.84/Y=157} равна
12/47
Задание номер 217. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.61/Y=154} равна
27/47
Задание номер 218. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.26/Y=101} равна
0,48
Задание номер 219. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=0.88/Y=163} равна
0,5
Задание номер 220. Двумерная случайная величина задана законом распределения. Тогда вероятность события P{X=1.01/Y=146} равна
0,5
Задание номер 89. По рации передаются три закодированных сообщения. Вероятность ошибки при расшифровке каждого сообщения составляет 0,3. Найти вероятность события: B= {одно сообщение расшифровано с ошибкой}. 0,441
|
|
Задание номер 90. По рации передаются три закодированных сообщения. Вероятность ошибки при расшифровке каждого сообщения составляет 0,3. Найти вероятность события: C= {с ошибкой расшифровано не менее двух сообщений}. 0,216
Задание номер 91. ОТК отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех взятых изделий только одно высшего сорта. 0,096
Задание номер 92. ОТК отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех взятых изделий два высшего сорта. 0,384
Задание номер 93. ОТК отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех взятых изделий хотя бы одно высшего сорта. 0,992
Задание номер 94. В гирлянду последовательно включено 10 лампочек. Вероятность перегорания лампочки при повышении напряжения составляет 0,1. Определить вероятность безотказной работы гирлянды при повышении напряжения. 0,349
Задание номер 95. Из урны, содержащей 6 белых и 4 черных шара, наудачу и последовательно извлекают по одному шару до появления черного шара. Найти вероятность того, что придется производить четвертое извлечение, если выборка производится с возвращением. 0,086
Задание номер 96. Из урны, содержащей 6 белых и 4 черных шара, наудачу и последовательно извлекают по одному шару до появления черного шара. Найти вероятность того, что придется производить четвертое извлечение, если выборка производится без возвращения. 0,095
Задание номер 97. Студент знает 40 из 60 вопросов программы. Экзаменационный билет состоит из 3 вопросов, отобранных случайным образом. Какова вероятность того, что студент знает не менее двух вопросов билета? 0,745
Задание номер 98. Коля с Мишей поочередно бросают монету, выигрывает тот, у кого раньше появится герб. Найти вероятности выигрыша каждого игрока, считая, что бросание монеты может продолжаться бесконечно долго, а Коля бросает первым. 2/3, 1/3
Задания номер 99-100. Вероятность наступления события в каждом опыте одинакова и равна 0,2. Опыты производились последовательно до наступления события. Определить вероятность того, что придется производить четвертый опыт. 0,512
Задание номер 101. Вычислительный центр, который должен производить непрерывную обработку поступающей информации, располагает тремя вычислительными устройствами. Каждое из этих устройств имеет вероятность отказа за некоторое время, равную 0.2. Найти вероятность того, что откажет только одно устройство. 0,384
Задание номер 102. Вероятность попадания в мишень при одном выстреле равна 0.7. После первого попадания стрельба прекращается. Найти вероятность того, что будет произведено 4 выстрела. 0,0189
Задание номер 103. Три орудия независимо друг от друга произвели залп по одной цели. Вероятность попадания первым орудием равна 0.6, вторым — 0.7, третьим — 0.8. Найти вероятность разрушения цели, если для этого достаточно хотя бы одного попадания. 0,976
Задание номер 104. Из колоды, содержащей 52 карты, берут наугад 2 карты. Найти вероятность того, что это будут карты одной масти. 0,0625
Задание номер 105. По результатам многолетних наблюдений установлено, что в сентябре бывает в среднем 14 солнечных дней. Найти вероятность того, что первого и второго сентября будет одинаковая погода. 0,5021
Задание номер 106. Абонент забыл последнюю цифру номера телефона и набирает ее наудачу. Найти вероятность того, что ему придется звонить не более, чем в 4 места. 0,4
Задание номер 107. Студент разыскивает нужную ему книгу последовательно в трех библиотеках. Вероятность того, что книга есть в первой библиотеке, равна 0.7; во второй — 0.9; в третьей — 0.6. Какова вероятность, что он найдет нужную книгу? 0,622
Задание номер 108. Студент разыскивает нужную ему книгу последовательно в трех библиотеках. Вероятность того, что книга есть в первой библиотеке, равна 0.7; во второй — 0.9; в третьей — 0.6. Какова вероятность того, что студенту придется посетить все три библиотеки. 0,378
Задание номер 109. В секретном замке на одной оси 4 диска, каждый из которых разделен на 5 секторов, на которых записаны различные цифры. Найти вероятность того, что при произвольной установке дисков получится нужная комбинация. 0,016
Задание номер 110. Найти вероятность того, что при залпе четырех стрелков, имеющих вероятности попадания соответственно 0.9, 0.8, 0.7, 0.6, будет три попадания. 0,4404
Задание номер 111. В цехе имеется три резервных мотора, работающих независимо друг от друга. Для каждого мотора вероятность того, что он в данный момент включен, равна 0.2. Найти вероятность того, что в данный момент включен хотя бы один мотор. 0,488
Задание номер 112. Вероятность попадания в мишень при одном выстреле равна 0.7. По мишени стреляют одиночными выстрелами до первого попадания. Найти вероятность того, что будет сделано не более трех выстрелов. 0,973
Задание номер 113. Три стрелка поочередно ведут стрельбу по одной и той же мишени до первого попадания. Каждый стрелок имеет 2 патрона. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0.2, для второго — 0.3, для третьего — 0.4. Найти вероятность того, что все три стрелка используют все патроны. 0,61
Задание номер 114. В магазин поступило 30% телевизоров фирмы L, остальное – фирмы N. В продукции фирмы L брак составляет 20% телевизоров; фирмы N – 15 %. Вероятность наудачу выбрать исправный телевизор составляет: 0,835
Задание номер 115. Имеются три партии деталей по 15 деталей в каждой. Число стандартных деталей в первой, второй и третьей партиях соответственно равно 11, 13, 12. Какова вероятность, что наудачу извлеченная деталь окажется бракованной? 0,198
Задание номер 116. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов? 0,1725
Задание номер 117. Имеются три одинаковые на вид урны; в первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных шара. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый. 0,64
Задание номер 118. По самолету производится три одиночных выстрела. Вероятность попадания при первом выстреле равна 0,4, при втором – 0,5, при третьем 0,7. Для вывода самолета из строя заведомо достаточно трех попаданий; при одном попадании самолет выходит из строя с вероятностью 0,2, при двух попаданиях – с вероятностью 0,6. Найти вероятность того, что в результате трех выстрелов самолет будет выведен из строя. 0,91
Задание номер 119. В магазин привозят товары от трех поставщиков: первый привозит 20%, второй - 30% и третий - 50% всего поступающего товара. Известно, что 10% товара первого поставщика высшего сорта, для второго и третьего поставщика эти значения равны 5% и 20%. Найти вероятность того, что случайно выбранный товар окажется высшего сорта. 0,135
Задание номер 120. В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразил мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. 0,85
Задание номер 121. В первой урне 7 белых и 3 черных шара, во второй – 8 белых и 2 черных. При перевозке из первой урны во вторую урну перекатились два шара. После того, как шары во второй урне перемешались, из неё выкатился шар. Найти вероятность того, что выкатившийся из второй урны шар белый. 0,635
Задание номер 122. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету). 0,67
123 задания вообще нет, 124 без формулировки задания, зато предоставлен ответ.
Задание номер 124. 0.0443
Задание номер 125. Из 30 стрелков 12 попадает в цель с вероятностью 0,6, 8 - с вероятностью 0,5 и 10 – с вероятностью 0,7. Наудачу выбранный стрелок произвел выстрел, поразив цель. Какая вероятность того что стрелок попал в мишень? 0,607
Задание номер 126. Фирма имеет три источника поставки комплектующих – фирмы А,В, С. На долю фирмы А приходится 50 % общего объема поставок, В– 30% и С– 20%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, фирмой В– 5% и С– 6%.Найти вероятность того, что наудачу выбранная деталь будет бракованной. 0,077
Задание номер 127. В первой урне 2 белых и 6 черных шаров, во второй – 4 белых и 2 черных. Из первой урны наудачу переложили 2 шара во вторую, после чего из второй урны наудачу достали один шар. Какова вероятность того, что этот шар белый? 0,5625
Задание номер 128. По данным переписи 1951 года, в Англии и Уэльсе среди отцов, имеющих сыновей, оказалось 13% темноглазых и 87% светлоглазых. У темноглазых отцов оказалось 39% темноглазых и 61% светлоглазых сыновей. У светлоглазых отцов оказалось 10% темноглазых и 90% светлоглазых сыновей. Какова вероятность того, что наугад выбранные среди этого населения отец и сын имеют глаза одинакового цвета? 0,78
Задание номер 129. Статистика показывает, что среди двоен оказывается 28% идентичных и 72% неидентичных близнецов. Среди идентичных близнецов 100% одного пола, 0% разного пола. Среди неидентичных близнецов 50% одного пола, 50% разного пола. Какова вероятность того, что наугад выбранные среди двоен близнецы имеют одинаковый пол? 0,64
Задание номер 130. Имеются три одинаковые урны. В первой урне находятся 4 белых, 4 чёрных и 4 красных шара, во второй – 4 белых, 6 чёрных и 8 красных шаров, а в третьей – 6 белых и 6 чёрных шаров. Наудачу выбирается урна и из нее наугад выбирается один шар. Выбранный шар оказался красным. Какова вероятность того, что этот шар вынут из второй урны? 0,6
Задание номер 131. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна стандартная деталь 0,67
Задание номер 132. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком 0,628
Задание номер 133. Есть три завода, производящих одну и ту же продукцию. При этом первый завод производит 25%, второй завод— 35% и третий— 40% всей производимой продукции. Брак составляет 5% от продукции первого завода, 3% от продукции второго и 4% от продукции третьего завода. Вся продукция смешивается и поступает в продажу. Найти условную вероятность того, что купленное изделие изготовлено первым заводом, если это изделие бракованное. 0,32
Задание номер 134. Есть три завода, производящих одну и ту же продукцию. При этом первый завод производит 25%, второй завод— 35% и третий— 40% всей производимой продукции. Брак составляет 5% от продукции первого завода, 3% от продукции второго и 4% от продукции третьего завода. Вся продукция смешивается и поступает в продажу. Найти условную вероятность того, что купленное изделие изготовлено вторым заводом, если это изделие бракованное. 0,27
Задание номер 135. Есть три завода, производящих одну и ту же продукцию. При этом первый завод производит 25%, второй завод— 35% и третий— 40% всей производимой продукции. Брак составляет 5% от продукции первого завода, 3% от продукции второго и 4% от продукции третьего завода. Вся продукция смешивается и поступает в продажу. Найти условную вероятность того, что купленное изделие изготовлено третьим заводом, если это изделие бракованное. 0,41
Задание номер 136. На завод поступают детали с трех предприятий 1- 50%, 2 - 20%, 3 - 30%. брак в деталях на первом = 0.05, на втором = 0.1, на третьем =0.15. найти вероятность того, что на заводе бракованные детали с первого завода. 0,278
Задание номер 137. На завод поступают детали с трех предприятий 1- 50%, 2 - 20%, 3 - 30%. брак в деталях на первом = 0.05, на втором = 0.1, на третьем =0.15. найти вероятность того, что на заводе бракованные детали с второго завода. 0,2
Задание номер 138. На завод поступают детали с трех предприятий 1- 50%, 2 - 20%, 3 - 30%. брак в деталях на первом = 0.05, на втором = 0.1, на третьем =0.15. найти вероятность того, что на заводе бракованные детали с третьего завода. 0,5
Задание номер 139. Из 30 стрелков 12 попадает в цель с вероятностью 0,6, 8 - с вероятностью 0,5 и 10 – с вероятностью 0,7. Наудачу выбранный стрелок произвел выстрел, поразив цель. Какая вероятность, что этот стрелок из первой группы? 0,395
Задание номер 140. Из 30 стрелков 12 попадает в цель с вероятностью 0,6, 8 - с вероятностью 0,5 и 10 – с вероятностью 0,7. Наудачу выбранный стрелок произвел выстрел, поразив цель. Какая вероятность, что этот стрелок из второй группы? 0,22
Задание номер 141. Из 30 стрелков 12 попадает в цель с вероятностью 0,6, 8 - с вероятностью 0,5 и 10 – с вероятностью 0,7. Наудачу выбранный стрелок произвел выстрел, поразив цель. Какая вероятность, что этот стрелок из третьей группы? 0,384
Задание номер 142. Имеются пять урн следующего состава: 2 урны по 2 белых и 3 черных шара, 2 урны по 1 белому и 4 черных шара, 1 урна— 4 белых и 1 черный шар. Из одной наудачу выбранной урны взят шар. Он оказался белым (событие A). Чему равна после опыта вероятность того, что шар вынут из урны третьего состава? 0,4
Задание номер 143. Имеются пять урн следующего состава: 2 урны по 2 белых и 3 черных шара, 2 урны по 1 белому и 4 черных шара, 1 урна— 4 белых и 1 черный шар. Из одной наудачу выбранной урны взят шар. Он оказался белым (событие A). Чему равна после опыта вероятность того, что шар вынут из урны второго состава? 0,2
Задание номер 144. Имеются пять урн следующего состава: 2 урны по 2 белых и 3 черных шара, 2 урны по 1 белому и 4 черных шара, 1 урна— 4 белых и 1 черный шар. Из одной наудачу выбранной урны взят шар. Он оказался белым (событие A). Чему равна после опыта вероятность того, что шар вынут из урны первого состава? 0,4
272. Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
273. Функцию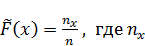 
, число вариантов со значением меньше x, n — объем выборки, называют эмпирической функцией распределения.
274. Отношение количества элементов в совокупности с одинаковым значением к объему совокупности называется относительной частотой варианты.
275. Количество элементов в совокупности с одинаковым значением называется частотой варианты.
276. Вариационным рядом называют упорядоченную по величине последовательность выборочных значений наблюдаемой случайной величины.
277. Выборка будет репрезентативной, если каждый объект выборки отобран случайно из генеральной совокупности и все объекты имеют одинаковую вероятность попасть в выборку.
278. Значения некоторого признака объектов в совокупности называют объемом.
279. Совокупность вариантов и соответствующих им частот (или относительных частот) в выборке называют статистическим распределением выборки.
280. Совокупность случайно отобранных объектов называют выборочной совокупностью (выборкой).
281. В ящике содержится 100 красных, 300 зеленых, 200 синих и 200 белых шаров. Из ящика наудачу извлекают 150 шаров. Объем генеральной совокупности составляет 800 шаров.
282. В ящике содержится 100 красных, 300 зеленых, 200 синих и 200 белых шаров. Из ящика наудачу извлекают 150 шаров. Объем выборки составляет 150 шаров.
283. Из генеральной совокупности извлечена выборка объема n = 80:
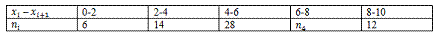
Тогда значение n4 равно: 20.
284. Из генеральной совокупности извлечена выборка объема n=100:
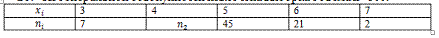
Тогда относительная частота варианты xi=4 равна: 25.
285. Из генеральной совокупности извлечена выборка объема n=81:
Тогда значение n3 равно: 34.
286. Статистическое распределение выборки имеет вид:
Тогда объем выборки равен: 67.
287. Статистическое распределение выборки имеет вид:
Тогда объем выборки равен: 150.
288. По выборке n = 200 построена гистограмма частот:
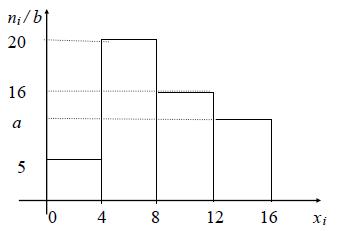
Чему равно значение а? Значение а равно: 9.
289. Для какой выборки, представленной в виде группированного статистического ряда, построен полигон частот? 
Для выборки из 15 элементов.
290. Как записывается эмпирическая функция распределения для выборочной случайной величины, заданной в виде статистического ряда?
F(xi)=ni/n
291. Генеральная совокупность - совокупность объектов, из которых производится выборка.
292. Выборка – это множество числовых значений, которые приняла исследуемая случайная величина в повторных независимых испытаниях.
293. Гистограмма — это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него.
294. Генеральная совокупность может иметь любое значение случайной величины.
295. Выборка – это набор числовых данных, количество которых определяется в повторных независимых испытаниях.
296. Гистограмма — это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него.
297. Генеральная совокупность может иметь любое значение случайной величины.
298. Полигон относительных частот - один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.
299. Что означает термин «репрезантивность» выборки?
Репрезантивность выборки означает, что каждый объект выборки отобран случайно из генеральной совокупности и все объекты имеют одинаковую вероятность попасть в выборку.
300. Упорядоченные по возрастанию наблюдаемые значения называются вариационным рядом.
301. Совокупность вариантов и соответствующих им частот (или относительных частот) в выборке называют статистическим распределением выборки.
302. Статистическая совокупность - это собрание единиц, обладающих массовостью, типичностью, качественной однородностью и наличием вариации.
303. Признак — это показатель, характеризующий некоторое свойство объекта совокупности, рассматриваемый как случайная величина.
304. Дискретный признак - это признак, который принимают отдельные значения, отличающиеся друг от друга на некоторую конкретную величину.
305. Ранжированный ряд распределения единиц - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака.
306. Если при проведении выборочного наблюдения выборочную совокупность формируют только из «лучших» представителей, какие ошибки возникают?
Ошибки репрезентативности.
307. На что влияет недостаточная численность выборки?
Недостаточная численность выборки влияет на точность вычислений.
308. Выборка называется репрезентативной, если каждый объект выборки отобран случайно из генеральной совокупности и все объекты имеют одинаковую вероятность попасть в выборку.
309. Выборка будет репрезентативной, если каждый объект выборки отобран случайно из генеральной совокупности и все объекты имеют одинаковую вероятность попасть в выборку.
310. Относительной частотой значения признака называется отношение частоты к объему совокупности данных.
Задание номер 311. Из генеральной совокупности извлечена выборка объема n=60. Тогда для эмпирической функции значение 3F*(4)·F*(6) равно
1.92 (48/25)
Задание номер 312. Из генеральной совокупности извлечена выборка объема n=50. Тогда для эмпирической функции значение 10F*(5)·F*(8) равно 
2.304 (288/125)
Задание номер 313. Из генеральной совокупности извлечена выборка объема n=60. Тогда для эмпирической функции значение 9F*(5)·F*(8) равно 
3.15 (63/20)
Задание номер 314. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(5) равно 
Задание номер 315. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3)·F*(5) равно
0.32 (8/25)
Задание номер 316. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(-1)·F*(5) равно
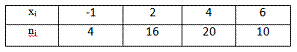
Задание номер 317. Из генеральной совокупности извлечена выборка объема g=60. Тогда для эмпирической функции значение 9F*(3)·F*(7) равно 
1.75 (7/4)
Задание номер 318. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3)·F*(7) равно 
0.64 (16/25)
Задание номер 319. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(5)·F*(9) равно 
Задание номер 320. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(21)·F*(27) равно
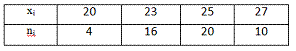
0.64 (16/25)
Задание номер 321. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(5)·F*(7) равно
0.736 (92/125)
Задание номер 322. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(6) равно 
Задание номер 323. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(13)·F*(16) равно
1.28 (32/25)
Задание номер 324. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3)·F*(5,7) равно
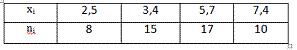
0.736 (92/125)
Задание номер 325. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(-2)·F*(3) равно
Задание номер 326. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(6,5)·F*(9) равно
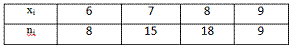
1.312 (164/125)
Задание номер 327. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3,5)·F*(7) равно
3.68 (92/25)
Задание номер 328. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(6)·F*(7,5) равно
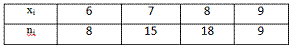
Задание номер 329. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2,5)·F*(5) равно
0.736 (92/125)
Задание номер 330. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3,5)·F*(5) равно
2.116 (529/250)
Задание номер 331. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(23)·F*(24) равно
0.552 (69/125)
Задание номер 332. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(11)·F*(13,6) равно
Задание номер 333. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(10)·F*(13) равно
0.96 (24/25)
Задание номер 334. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2,5)·F*(5) равно
0.46 (23/50)
Задание номер 335. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(9)·F*(12,5) равно
Задание номер 336. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3)·F*(6) равно
1.28 (32/25)
Задание номер 337. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(7) равно
1.28 (32/25)
Задание номер 338. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3)·F*(5) равно
0.736 (92/125)
Задание номер 339. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(8) равно
1.28 (32/25)
Задание номер 340. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(7) равно
Задание номер 341. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(5) равно
0.616 (77/125)
Задание номер 342. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(7) равно
0.64 (16/25)
Задание номер 343. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(1)·F*(7) равно
Задание номер 344. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(7) равно
1.28 (32/25)
Задание номер 345. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3)·F*(7) равно
1.28 (32/25)
Задание номер 346. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(3)·F*(5) равно
0.736 (92/125)
Задание номер 347. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(4,5)·F*(5) равно
2.116 (529/250)
Задание номер 348. Из генеральной совокупности извлечена выборка объема g=50. Тогда для эмпирической функции значение 10F*(2)·F*(8) равно