Следствие 1. Теорема 11 (теорема Коши для многосвязной области).
 Если функция
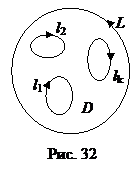
Если функция  аналитическая в многосвязной области D, ограниченной контуром L и внутренними по отношению к нему контурами l 1, l 2,…, l k и непрерывна в замкнутой области
аналитическая в многосвязной области D, ограниченной контуром L и внутренними по отношению к нему контурами l 1, l 2,…, l k и непрерывна в замкнутой области 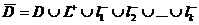 (рис. 32), где знаки в верхних индексах означают направления обходов, то
(рис. 32), где знаки в верхних индексах означают направления обходов, то

 или
или  . (21)
. (21)
 или
или 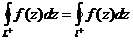 , (рис. 33). (21/)
, (рис. 33). (21/)
Следствие 2. Интегралы от аналитических функций вдоль любых двух кусочно-гладких кривых с общим началом z 0 и концом z 1 равны.
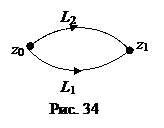
 , если
, если  замкнутый контур (рис. 34).
замкнутый контур (рис. 34).
Следствие 3. Интеграл от аналитической функции, заданной в односвязной области D, зависит только от начальной и конечной точек пути интегрирования:

Следствие 4. Интеграл  при фиксированном z 0 является функцией верхнего предела:
при фиксированном z 0 является функцией верхнего предела:  Ф (z), где Ф (z) является аналитической в области D и Ф /(z) = f (z). Следствие 5. Если
Ф (z), где Ф (z) является аналитической в области D и Ф /(z) = f (z). Следствие 5. Если  – аналитическая функция в односвязной области D, то Ф (z) называется первообразной или неопределенным интегралом от функции
– аналитическая функция в односвязной области D, то Ф (z) называется первообразной или неопределенным интегралом от функции  , причем если F (z) – одна из первообразных для
, причем если F (z) – одна из первообразных для  , то
, то  . (22)
. (22)
Теорема 12 (интегральная формула Коши).
 Значение функции
Значение функции  , аналитической в односвязной области D, в особой точке
, аналитической в односвязной области D, в особой точке  определяется ее значениями на любом замкнутом кусочно-гладком контуре l, охватывающем точку z 0 , целиком лежащем вместе со своей внутренностью в области D (рис. 35), и вычисляется по формуле:
определяется ее значениями на любом замкнутом кусочно-гладком контуре l, охватывающем точку z 0 , целиком лежащем вместе со своей внутренностью в области D (рис. 35), и вычисляется по формуле:
 .
.
При этом функция  имеет всюду в D производные любого порядка, для которых справедливы формулы:
имеет всюду в D производные любого порядка, для которых справедливы формулы:
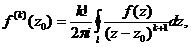 k =1, 2,… (23)
k =1, 2,… (23)
Замечание 1. Из формулы (23) можно найти значение криволинейного интеграла вида:
 , (24)
, (24)
где z 0 – особая точка функции  , лежащая внутри контура l.
, лежащая внутри контура l.
Замечание 2. 
Следствие (из теоремы 12). Если функция  аналитическая в замкнутой односвязной области
аналитическая в замкнутой односвязной области  , где L – граница области D,
, где L – граница области D,  , то имеет место формула:
, то имеет место формула:

Замечание. При вычислении интеграла вида  , где
, где  аналитическая функция в односвязной области
аналитическая функция в односвязной области 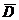 ,
,  – многочлен, не имеющий нулей на контуре L, удобно пользоваться правилами:
– многочлен, не имеющий нулей на контуре L, удобно пользоваться правилами:
1) Если в области D нет нулей многочлена  , то по формуле (20)
, то по формуле (20)  .
.
2) Если в области D расположен один простой нуль z = z 0 многочлена  , тогда
, тогда 
 , где f (z) – аналитическая функция в области
, где f (z) – аналитическая функция в области 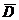 .
.
3) Если в области D расположен один кратный нуль z = z 0 многочлена  кратности k, тогда
кратности k, тогда 
 , где f (z) – аналитическая функция в области
, где f (z) – аналитическая функция в области 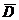 .
.
4) Если в области D расположено два нуля z = z 1, z = z 2 многочлена  , то по формуле (21)
, то по формуле (21) 

 , где l 1 и l 2 – границы непересекающихся окрестностей точек z = z 1, z = z 2.
, где l 1 и l 2 – границы непересекающихся окрестностей точек z = z 1, z = z 2.
Теорема 13 (теорема Лиувилля).
Если функция  аналитическая и ограниченная во всей плоскости Гаусса, то
аналитическая и ограниченная во всей плоскости Гаусса, то  .
.
Пример 3. В ычислить интеграл по заданному контуру:  , где
, где 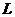 :
:  .
.
Решение.
Контур L:  – уравнение окружности с центром в начале координат и радиусом
– уравнение окружности с центром в начале координат и радиусом  . D – область внутри окружности (рис. 36).
. D – область внутри окружности (рис. 36).
 Найдем особые точки подынтегральной функции
Найдем особые точки подынтегральной функции 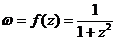 , т.е. точки, где знаменатель обращается в нуль:
, т.е. точки, где знаменатель обращается в нуль: 



 ,
,  особые точки. Данные точки не лежат внутри контура интегрирования L (рис. 35), т.е.
особые точки. Данные точки не лежат внутри контура интегрирования L (рис. 35), т.е.  . Следовательно, по теореме Коши (формула 19 или по правилу 1 замечания),
. Следовательно, по теореме Коши (формула 19 или по правилу 1 замечания), 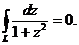
Пример 4. В ычислить интеграл по заданному контуру:  .
.
Решение.


 – уравнение окружности с центром в точке z = i и радиусом 1. D 1 – область внутри окружности (рис. 37).
– уравнение окружности с центром в точке z = i и радиусом 1. D 1 – область внутри окружности (рис. 37).  ,
,  особые точки подынтегральной функции
особые точки подынтегральной функции 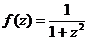 (нашли в примере 3). Из них точка
(нашли в примере 3). Из них точка  , точка
, точка  .
.
Поэтому рассмотрим многосвязную область D, ограниченную окружностью  и внутренним контуром
и внутренним контуром  (рис. 38).
(рис. 38).
Тогда в этой области функция 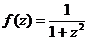 аналитическая, и по следствию 1 (теореме Коши для многосвязной области (формула (21/)) можем записать, что
аналитическая, и по следствию 1 (теореме Коши для многосвязной области (формула (21/)) можем записать, что 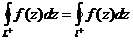 , т.е.
, т.е.  =
=  .
.
Данный интеграл вычислим при помощи интегральной формулы Коши (24):  . Для этого выделим в знаменателе особую точку:
. Для этого выделим в знаменателе особую точку:  =
= 
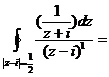 (k = 0,
(k = 0,  ) =
) =  =
= 
Замечание. Данный пример можно решить, используя следствие к теореме 12, не выделяя внутреннюю область, ограниченную контуром l или по правилу 2 предыдущего замечания.
 Пример 5. В ычислить интеграл по заданному контуру:
Пример 5. В ычислить интеграл по заданному контуру:  .
.
Решение.
 – уравнение окружности с центром в точке z = i и радиусом 3. D 1 – область внутри окружности (рис. 39).
– уравнение окружности с центром в точке z = i и радиусом 3. D 1 – область внутри окружности (рис. 39).

 ,
,  особые точки функции
особые точки функции 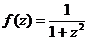 (нашли в примере 3). Они обе лежат внутри контура. Поэтому рассмотрим многосвязную область D, ограниченную окружностью
(нашли в примере 3). Они обе лежат внутри контура. Поэтому рассмотрим многосвязную область D, ограниченную окружностью  и двумя внутренними контурами
и двумя внутренними контурами  и
и  (рис. 40).
(рис. 40).
Тогда в этой области функция 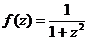 аналитическая, и по следствию 1 (теореме Коши для многосвязной области (формула (21/)) можем записать, что
аналитическая, и по следствию 1 (теореме Коши для многосвязной области (формула (21/)) можем записать, что  , т.е.
, т.е.
 =
= 
 = (выделим в знаменателях особые точки) =
= (выделим в знаменателях особые точки) =
=  +
+ 


 =
=  .
.
Пример 6. В ычислить интеграл по заданному контуру:  .
.
Решение.

 – уравнение окружности с центром в точке z = – i и радиусом 2. D 1 – область внутри окружности (рис. 41).
– уравнение окружности с центром в точке z = – i и радиусом 2. D 1 – область внутри окружности (рис. 41).
Найдем особые точки: 

 ,
,  – особые точки, причем
– особые точки, причем  имеет кратность равную 2.
имеет кратность равную 2.
Знаменатель обращается в нуль внутри контура в особой точке  вторая особая точка
вторая особая точка  . Тогда в области D функция
. Тогда в области D функция  аналитическая, за исключением нуля, и по следствию к теореме 12 или правилу 3 из замечания к следствию можем записать, что
аналитическая, за исключением нуля, и по следствию к теореме 12 или правилу 3 из замечания к следствию можем записать, что
 =
= 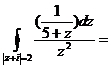
 (k = 1,
(k = 1,  ) =
) =
=  .
.