Глава 2
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
§ 1. Основные свойства определенных интегралов
и их вычисление
1. Пусть на отрезке [ a, b ] определена функция f (x). Интегральной суммой называется
 ,
,
где a < x 0 < x 1 <… < xn = b, ∆ xi = xi –1 – xi, ξ i Î [ xi –1, xi ], i = 1, 2, …, n.
Определенным интегралом от функции f (x) на отрезке [ a, b ] называется предел интегральных сумм
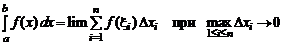 ,
,
при условии, что предел не зависит от выбора точек ξ i Î[ xi -1, xi ] и способов разбиения отрезка на части.
Если этот предел существует, функция называется интегрируемой на отрезке [ a, b ]. Известно, что непрерывные на отрезке функции интегрируемы. Интегрируемыми будут также ограниченные на отрезке функции, имеющие конечное число разрывов первого рода.
Перечислим основные свойства определенных интегралов.
1. 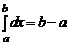 .
.
2. По определению считают, что
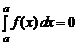 ,
, 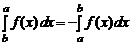 , a < b.
, a < b.
3. Линейные свойства определенного интеграла
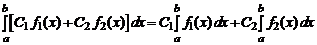 ,
,
где C 1 и C 2 – постоянные.
4. Если функция f (x) интегрируема на отрезке [ a, b ], то она будет интегрируемой на любом отрезке [a, b] Ì [ a, b ].
5. Аддитивность определенного интеграла. Пусть a, b, c – некоторые числа. A = min{ a, b, c }, B = max{ a, b, c } и пусть функция f (x) интегрируема на отрезке [ A, B ]. Тогда выполняется равенство
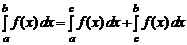 .
.
6. Если f (x) ≤ g (x) на [ a, b ], то
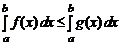 .
.
В частности, если f (x) ³ 0 на [ a, b ], то
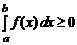 .
.
Теорема о среднем. Если функция f (x) непрерывна на отрезке
[ a, b ], то на этом отрезке найдется такая точка x 0, что
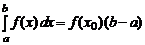 .
.
Определенный интеграл 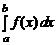 при f (x) ³ 0 на отрезке [ a, b ] численно равен площади криволинейной трапеции
при f (x) ³ 0 на отрезке [ a, b ] численно равен площади криволинейной трапеции
D = {(x, y): a ≤ x ≤ b, 0 ≤ y ≤ f (x)}.
В этом заключается геометрический смысл определенного интеграла.
Формула Ньютона–Лейбница. Если F (x) – первообразная функции f (x), то определенный интеграл от f (x)по отрезку [ a, b ] можно вычислить по формуле Ньютона–Лейбница
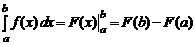 .
.
Формула Ньютона – Лейбница позволяет привлекать для вычисления определенных интегралов все приемы и методы, используемые при вычислении неопределенных интегралов. Формула Ньютона – Лейбница есть следствие следующего утверждения.
Если F (x) есть первообразная функции f (x) на отрезке [ a, b ], то в каждой точке x Î (a, b) непрерывности функции f (x) выполняется равенство
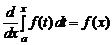 .
.
Из этого утверждения и теоремы о дифференцировании сложной функции следует, что
 .
.
Аналогичные утверждения справедливы также и для переменного нижнего предела интеграла: в каждой точке x непрерывности функции f (x) выполняется равенство
 .
.
Если функцияj (x) дифференцируема на интервале [a, b] и такая, что t = j (x) Î (a, b) при x Î (a, b), то выполняется равенство
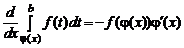 .
.
Из утверждений о дифференцировании интеграла с переменными пределами и из свойства аддитивности определенного интеграла следует, что
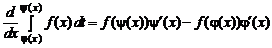 .
.
Рассмотрим примеры.
Вычислить с помощью формулы Ньютона–Лейбница интегралы.
1.1.  .
.
Решение. Используя линейные свойства интеграла и табличные интегралы, находим первообразную и вычисляем интеграл
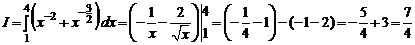 .
.
1.2.  .
.
Решение. Находим первообразную и применяем формулу Ньютона–Лейбница.
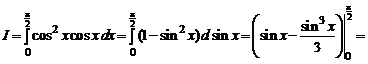
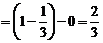 .
.
1.3. 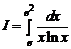 .
.
Решение. Ищем первообразную для функции 
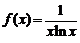 и применяем формулу Ньютона–Лейбница
и применяем формулу Ньютона–Лейбница
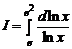 =
= 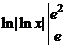 =
=  = ln2 – ln1 = ln2.
= ln2 – ln1 = ln2.
1.4. Выяснить (не вычисляя), какой из интегралов больше:
а)  или
или  ;
;
б)  или
или 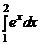 .
.
Решение.
а) Поскольку при 0 < x < 1 выполняется 0< x 2 < x, то в силу свойств показательной функции выполняется 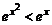 . Тогда из свойства 6 определенных интегралов следует
. Тогда из свойства 6 определенных интегралов следует
 ≤
≤ 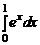 .
.
б) При 1 < x < 2 выполняется x ≤ x 2. Тогда 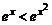 и, следовательно,
и, следовательно,
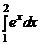 ≤
≤  .
.
1.5. Оценить интеграл
 .
.
Решение. Так как при 0 ≤ x ≤ 1 выполняется
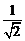 ≤
≤ 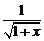 ≤ 1,
≤ 1,
то из неравенств
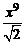 ≤
≤ 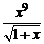 ≤ x 9
≤ x 9
и свойств интеграла следует
 ≤
≤ 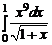 ≤
≤ 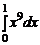 ,
,
откуда, учитывая, что 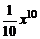 – первообразная для x 9, находим
– первообразная для x 9, находим
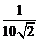 ≤
≤ 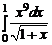 ≤
≤  .
.
1.6. Найти производную по x от следующих функций:
а) 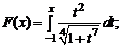 б)
б) 
в)  , x > 1; г)
, x > 1; г) 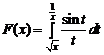 , x Î(0, ¥).
, x Î(0, ¥).
Решение.
а) 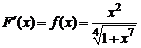 ; б)
; б) 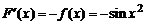 ;
;
в) 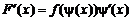 =
= 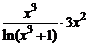 =
= 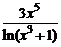 ;
;
г) 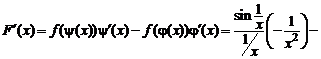
 .
.
Часто, если это не приводит к недоразумениям, пишут 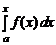 , а не
, а не 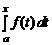 . Мы, следуя традиции, будем писать так же.
. Мы, следуя традиции, будем писать так же.
1.7. Найти пределы:
а) 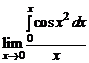 ; б)
; б)  .
.
Решение.
а) Так как 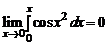 , то имеем неопределенность вида
, то имеем неопределенность вида 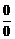 . Применим правило Лопиталя:
. Применим правило Лопиталя:
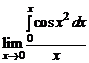 =
= 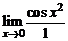 = cos 0 = 1.
= cos 0 = 1.
б) В этом примере также применим правило Лопиталя:
 =
= 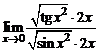 =
= 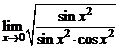 =
= 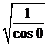 = 1.
= 1.
1.8. Найти многочлен P (x) наименьшей степени, имеющий минимум, равный –25 при x = 2, и максимум, равный 2 при x = –1.
Решение. Многочлен есть дифференцируемая функция на всей числовой оси. Поэтому точки экстремума могут быть только среди корней производной P ¢(x), которая также есть многочлен. Поскольку нам известно, что P ¢(–1) = 0 и P ¢(2) = 0, то P ¢(x) есть многочлен степени не меньше двух. Значит, P ¢(x) следует искать среди многочленов второй степени. Тогда P ¢(x) = a (x + 1)(x – 2) = ax 2– ax – 2 a. Отсюда находим
P (x) = 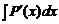 =
= 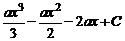 .
.
Так как по условию P (–1) = 2, P (2) = –25, мы получаем систему уравнений для нахождения a и C:
P (–1) = 2 = 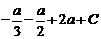 ,
,
P (2) = –25 = 
или
2 =  ,
,
–25 = 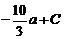 .
.
Решая систему, находим a = 6, C = –5. Следовательно, P (x) = 2 x 3 – 3 x 2 – – 12 x – 5.
Замена переменной в определенном интеграле
Пусть на отрезке [ a, b ] определена интегрируемая функция f (x) и пусть функция x = j(t) определена на отрезке [a, b] и имеет на нем непрерывную производную j ¢ (t) и значения x = j(t) принадлежат отрезку [ a, b ], когда t пробегает отрезок [a, b]. Тогда справедлива формула замены переменной в определенном интеграле
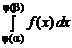 =
= 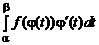 .
.
Если функция x = j(t) строго возрастает, то j(a) < j(b), a ≤ t ≤ b, если убывает, то j(a) > j(b). Если x = j(t) возрастает и j(a) = a, j(b) = b, то формула замены переменной принимает вид
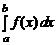 =
= 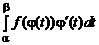 .
.
Если x = j(t) убывает и j(a) = b, j(b) = a, то формула замены переменной выглядит так:
 =
= 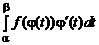 .
.
Отметим, что в отличие от неопределенных интегралов после замены переменной и вычисления интеграла возврат к старой переменной не требуется.
Вычислить следующие интегралы.
1.9. 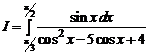 ; 1.10.
; 1.10. 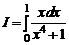 ;
;
1.11.  ; 1.12.
; 1.12. 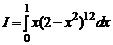 ;
;
1.13.  ; 1.14.
; 1.14. 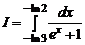 ;
;
1.15.  ; 1.16.
; 1.16.  ;
;
1.17. 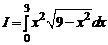 ; 1.18.
; 1.18.  .
.
Решение.
1.9. Делаем замену переменной cos x = t, –sin x dx = dt;  соответствует
соответствует  ,
,  соответствует t = 0. Получаем
соответствует t = 0. Получаем
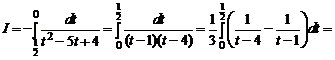
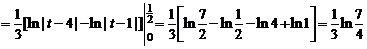 .
.
1.10. Делаем замену переменной
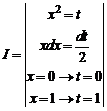 =
= 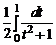 =
= 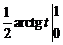 =
=  .
.
1.11.
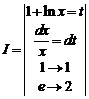 =
= 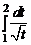 =
= 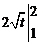 =
=  .
.
1.12.
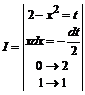 =
= 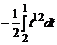 =
= 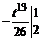 =
=  =
=  .
.
1.13.
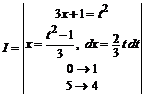 =
=  =
= 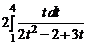 =
=
= 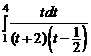 =
= 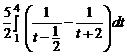 =
= 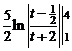 =
=
= 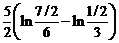 =
=  .
.
1.14.
 =
= 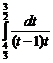 =
= 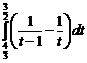 =
=  =
=
= 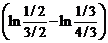 =
= 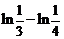 =
=  .
.
1.15.
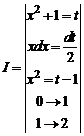 =
= 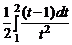 =
= 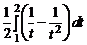 =
= 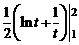 =
=
= 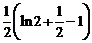 =
= 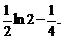
1.16.
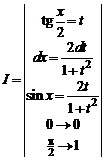 =
=  =
= 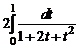 =
=
=  =
= 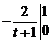 = –1 + 2 = 1.
= –1 + 2 = 1.
1.17.
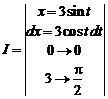 =
= 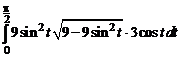 =
= 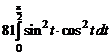 =
=
=  =
= 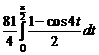 =
= 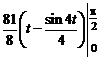 =
= 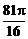 .
.
1.18.
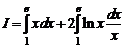 =
= 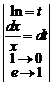 =
= 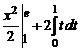 =
= 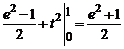 .
.
1.19.
А. Доказать, что если f (x) – четная функция, то
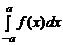 =
=  .
.
Б. Доказать, что если f (x) – нечетная функция, то
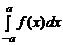 = 0.
= 0.
Решение.
А. Представим интеграл по отрезку [– a, a ] в виде суммы интегралов
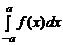 =
=  +
+ 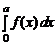 .
.
Сделаем в первом интеграле справа замену переменной x = – t. Тогда dx = – dt, x = – a соответствует t = a, x = 0 соответствует t = 0. Отсюда следует
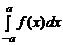 =
= 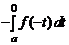 +
+ 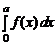 .
.
Так как функция четная, то f (– t)= f (t). Поэтому
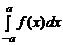 =
= 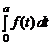 +
+ 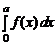 = 2
= 2 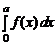 .
.
Б. Как и в примере А, запишем
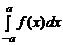 =
=  +
+ 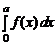 .
.
Сделаем в первом интеграле справа замену переменной x = – t. Тогда
 = –
= –  .
.
Так как функция f нечетная, то f (– t) =– f (t). Поэтому
 =
= 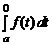 =
= 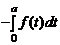 .
.
Отсюда следует утверждение Б.
1.20. Вычислить интегралы:
а)  ;
;
б) 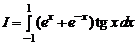 ;
;
в) 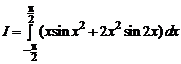 .
.
Решение.
а) f (x) =  . Тогда
. Тогда
f (– x) = 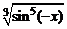 =
=  = –
= –  = – f (x).
= – f (x).
Значит, функция f (x) – нечетная и по задаче 1.19 Б I = 0;
б) f (x) = (ex + ex) tg x, f (– x) = (e – x + ex) tg (– x) = – f (x). Согласно результатам задачи 1.19 Б I = 0;
в) f (x) = x sin x 2 + 2 x 2 sin 2 x. Оба слагаемых в этом выражении являются произведениями нечетной функции на четную, т. е. нечетными функциями. Из задачи 1.19 Б следует, что и в этом случае I =0.
Интегрирование по частям
Пусть u и v – функции, определенные на отрезке [ a, b ] и имеющие на нем непрерывные производные u ¢и v ¢. Тогда справедлива формула интегрирования по частям в определенном интеграле
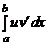 =
=  –
–  ,
,
где  = u (b) v (b) – u (a) v (a). Формулу можно переписать в более простом виде
= u (b) v (b) – u (a) v (a). Формулу можно переписать в более простом виде
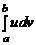 =
=  –
– 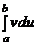 .
.
1.21. Вычислить интегралы:
а) 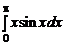 ; б)
; б)  ; в)
; в) 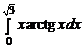 ;
;
г) 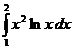 ; д)
; д) 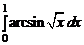 .
.
Решение.
а) применяем формулу интегрирования по частям
 =
= 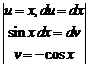 =
=  =
=
= – p cos p+  = p.
= p.
б) полагаем u = arccos x. Тогда
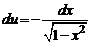 , v = x,
, v = x,
и мы получаем
 = arcos 1 –
= arcos 1 – 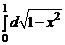 =
= 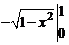 =1;
=1;
в) 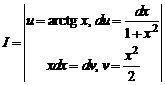 =
=  =
=
= 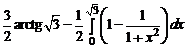 =
= 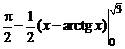 =
=
= 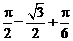 =
= 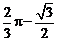 ;
;
г) 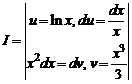 =
= 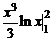 –
– 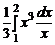 =
= 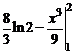 =
=
=  =
=  ;
;
д) этот интеграл, как это часто бывает, можно вычислить разными способами. Если сделать сначала замену переменной  = t, то мы придем к интегралу
= t, то мы придем к интегралу  , который после интегрирования по частям приводит к интегралу
, который после интегрирования по частям приводит к интегралу 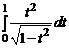 .
.
Если сразу применить формулу интегрирования по частям (u =
= arcsin  , v = x) то получим
, v = x) то получим
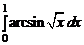 = x arcsin
= x arcsin 
 –
– 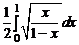 .
.
Интеграл в правой части рационализируется подстановкой  . Мы вычислим интеграл с помощью подстановки arcsin
. Мы вычислим интеграл с помощью подстановки arcsin  = t. Тогда x = sin2 t, d x = 2sin t cos t dt= sin2 t dt, x = 0 соответствует t = 0,
= t. Тогда x = sin2 t, d x = 2sin t cos t dt= sin2 t dt, x = 0 соответствует t = 0,
x = 1 соответствует 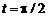 . Получаем
. Получаем
 =
= 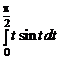 .
.
Вычислим получившийся интеграл по частям:
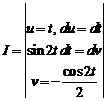 =
= 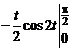 +
+  =
=  =
= 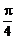 .
.
Последний способ решения оказался более экономичным по сравнению с двумя рассмотренными выше.
Рекуррентные формулы
В этом пункте мы рассмотрим несколько примеров, в которых с помощью интегрирования по частям получаются рекуррентные формулы для определенных интегралов.
1.22. Вычислим интеграл 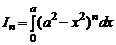 , где n – натуральное число.
, где n – натуральное число.
Решение. Разложение подынтегральной функции по формуле бинома Ньютона приводит к громоздким выкладкам. Проще вывести рекуррентную формулу. Представим интеграл In в виде
 =
=  –
– 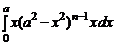 .
.
Последний интеграл проинтегрируем по частям:
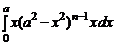 =
= 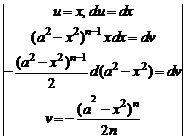 =
=
=  +
+ 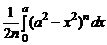 =
= 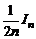 .
.
Таким образом,
In = 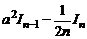 .
.
Отсюда вытекает
In =  In -1.
In -1.
Очевидно, что I 0 = a. Отсюда получаем
In =  In –1 =
In –1 = 
 In –2 =
In –2 = 

 In –3 =…
In –3 =…
...= a 2n+1 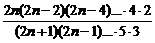 .
.
Принято обозначать 1×3×5×…×(2 n + 1) = (2 n + 1)!!, 2 ×4 × …×(2 n) = (2 n)!!. Тогда интеграл равен
In = a 2 n +1  .
.
Замечание. При выводе формулы
In =  In -1
In -1
нигде не использовалось то, что n – натуральное число. В действительности эта формула справедлива для любых действительных n, отличных от 0 и от  .
.
1.23. Вычислить интеграл 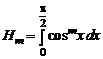 , где m – натуральное число.
, где m – натуральное число.
Решение. Сделаем подстановку 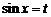 :
:
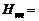

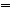
 .
.
Здесь 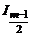 – интеграл из предыдущей задачи 1.22. Но
– интеграл из предыдущей задачи 1.22. Но 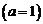

Следовательно,
 .
.
Если m – нечетное число, то полученная рекуррентная формула сводит 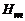 к
к
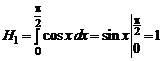 ,
,
поэтому при 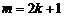
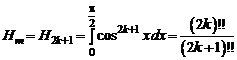 .
.
Если 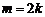 – четное число, то рекуррентная формула сводит
– четное число, то рекуррентная формула сводит 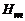 к
к
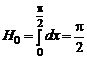 ,
,
поэтому
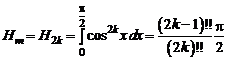 .
.
Замечание. С помощью подстановки 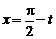 легко убедиться, что
легко убедиться, что
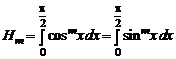 .
.
1.24. Вычислить интеграл
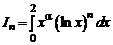 ,
,
где 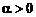 ; n – натуральное число.
; n – натуральное число.
Решение. Отметим прежде всего, что хотя подынтегральная функция 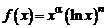 не имеет смысла при
не имеет смысла при 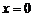 , тем не менее, положив
, тем не менее, положив  , мы получаем функцию, непрерывную на
, мы получаем функцию, непрерывную на  . Действительно,
. Действительно,
 ,
,
что легко проверяется с помощью правила Лопиталя. Применяем формулу интегрирования по частям:
 =
= 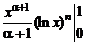 –
– 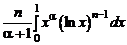 .
.
Таким образом, получаем
 .
.
Отсюда вытекает
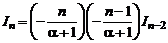 =…=
=…=  .
.
Так как
 ,
,
то окончательно получаем
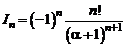 .
.
1.25. Вычислить интеграл
 ,
,
где 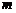 и
и 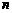 – целые неотрицательные числа.
– целые неотрицательные числа.
Решение. Вычисляем интеграл по частям:
 =
= 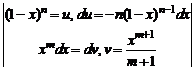 =
=
= 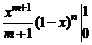 +
+  .
.
Отсюда получаем
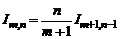 .
.
Отметим, что полученная формула справедлива не только для целых 
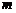 и
и 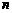 , а для всех
, а для всех  и
и 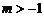 . Если
. Если 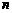 – натуральное число, то, применяя формулу несколько раз, запишем
– натуральное число, то, применяя формулу несколько раз, запишем
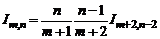 =…=
=…= 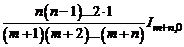 ,
,
но
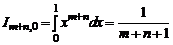 .
.
Следовательно,
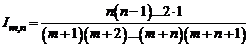 =
= 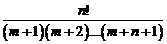 .
.
Если 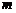 – тоже целое неотрицательное число, то отсюда получаем
– тоже целое неотрицательное число, то отсюда получаем
 =
= 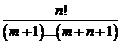 =
=  =
=  ,
,
где  – число сочетаний из m + n + 1 по n.
– число сочетаний из m + n + 1 по n.
Задачи для самостоятельного решения
Вычислить следующие интегралы.
1.26. 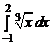 ; 1.27.
; 1.27. 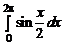 ; 1.28.
; 1.28. 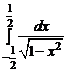 ;
;
1.29. 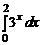 ; 1.30.
; 1.30. 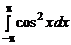 ; 1.31.
; 1.31.  .
.
1.32. Выяснить (не вычисляя), какой из интегралов больше:
а) 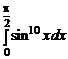 или
или 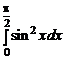 ; б)
; б) 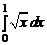 или
или 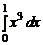 ;
;
в) 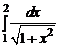 или
или  .
.
1.33. Оценить интеграл
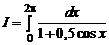 .
.
1.34. Доказать неравенства
1 <  < e.
< e.
1.35. Найти производную:
а) 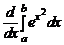 ; б)
; б) 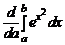 ; в)
; в) 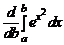 .
.
1.36. Найти пределы:
а) 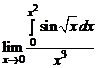 ; б)
; б) 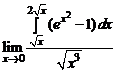 .
.
Вычислить интегралы (1.37)–(1.43)
1.37.  . 1.38.
. 1.38.  . 1.39.
. 1.39. 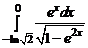 .
.
1.40. 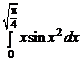 . 1.41.
. 1.41. 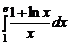 . 1.42.
. 1.42.  ;
;
1.43.  .
.
Вычислить следующие интегралы, используя пример 1.19:
1.44.  ; 1.45.
; 1.45. 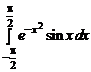 ;
;
1.46. 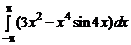 .
.
Вычислить следующие интегралы:
1.47. 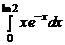 ; 1.48.
; 1.48.  ;
;
1.49.  ; 1.50.
; 1.50. 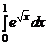 .
.
1.51. Пусть
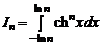 , n = 3,4…
, n = 3,4…
Доказать рекуррентную формулу
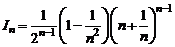 +
+ 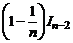 .
.
1.52. Вычислить интеграл
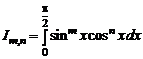 ,
,
где m, n – целые неотрицательные числа.
§ 2. Несобственные интегралы с бесконечными пределами
интегрирования
Пусть функция f (x) определена для всех x ³ а и интегрируема на любом отрезке [ a, b ]. Если существует
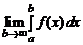 ,
,
то этот предел называется несобственным интегралом функции f (x) на луче [ a, b) и обозначается 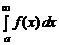 . В этом случае говорят, что несобственный интеграл
. В этом случае говорят, что несобственный интеграл 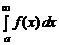 сходится, а функция f (x) интегрируема в несобственном смысле на [ a,
сходится, а функция f (x) интегрируема в несобственном смысле на [ a,  ).
).
Если предел при b ® ¥ не существует, то интеграл 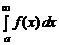 называется расходящимся.
называется расходящимся.
Аналогично определяется несобственный интеграл от функции f (x), x Î(– ¥, b ], с нижним бесконечным пределом интегрирования:
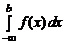 =
=  .
.
Несобственный интеграл с бесконечными верхним и нижним пределами интегрирования функции f (x), x Î (– ¥, ¥), определяется следующим образом:
 =
= 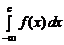 +
+ 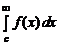 ,
,
где c – некоторое число. Предполагается, что на любом отрезке [ A, B ]Ì(– ¥, ¥) существует интеграл 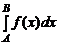 в собственном, обычном смысле. Если интеграл
в собственном, обычном смысле. Если интеграл  существует для некоторого c Î(– ¥, ¥), то он существует и для любого другого c ¢Î(– ¥, ¥) и в этом случае
существует для некоторого c Î(– ¥, ¥), то он существует и для любого другого c ¢Î(– ¥, ¥) и в этом случае
 =
= 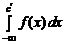 +
+ 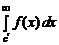 .
.
Иногда несобственный интеграл от f (x) по (– ¥, ¥) определяют следующим образом:
 =
= 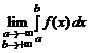 .
.
Можно показать, что оба определения несобственного интеграла  эквивалентны.
эквивалентны.
Основные формулы для несобственных интегралов
Линейность интеграла. Если несобственные интегралы
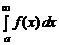 ,
, 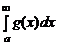
сходятся, то для любых чисел M и N сходится интеграл
 ,
,
причем
 =
= 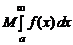 +
+  .
.
Формула Ньютона–Лейбница. Если функция f (x), a ≤ x < ¥, непрерывна и F (x) – какая-либо ее первообразная, то
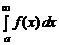 =
= 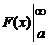 = F (+¥) – F (a),
= F (+¥) – F (a),
где
F (+ ¥) =  .
.
Формула замены переменной. Пусть f (x), a ≤ x < ¥, – непрерывная функция, j(t), a ≤ t < b, – функция с непрерывной на интервале  производной j¢(t), причем
производной j¢(t), причем
j(a) = a, a < j (t) < 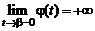 ,
,
тогда
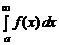 =
= 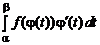 .
.
Формула интегрирования по частям. Если u (x) и v (x), a ≤ x < ¥, непрерывно дифференцируемы и 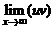 существует, то
существует, то
 =
=  –
– 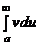 ,
,
где
 =
= 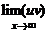 – u (a) v (a).
– u (a) v (a).
Перечисленные свойства верны и для интегралов по лучу ( или по прямой
или по прямой 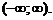
Рассмотрим примеры.
Вычислить следующие интегралы или установить их расходимость.
2.1. 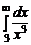 . 2.2.
. 2.2. 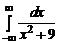 . 2.3.
. 2.3. 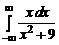 .
.
2.4.  . 2.5.
. 2.5. 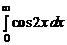 . 2.6.
. 2.6.  .
.
2.7. 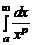 , a >0. 2.8.
, a >0. 2.8.  . 2.9.
. 2.9.  .
.
Решение.
2.1. 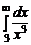 =
= 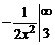 =
= 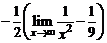 =
=  .
.
2.2. 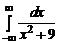 =
=  =
= 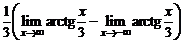 =
=
= 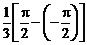 =
=  .
.
2.3. 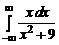 =
= 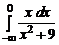 +
+ 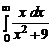 .
.
Интеграл в левой части равенства сходится только в том случае, если сходятся