Лабораторная работа. Дискретно косинусное преобразование и алгоритм сжатия изображений

Лабораторная работа

Дискретно косинусное преобразование и алгоритм сжатия изображений

При решении многих задач пространственный сигнал В_а(x,y) удобно представлять в виде суммы гармонических составляющих F(w_x,w_y), получаемых, например, с помощью преобразований Фурье.

Тесно связанное с преобразованием Фурье Дискретное косинусное преобразование (ДКП, DCT - англ. Discrete Cosine Transform) применяется в алгоритмах сжатия JPEG и MPEG. Математически преобразование можно осуществить умножением вектора на матрицу преобразования. При этом матрица обратного преобразования с точностью до множителя равна транспонированной матрице. В математике матрицы выбирают так, чтобы преобразование было ортонормированным, а постоянный множитель равен единице. В компьютерных приложениях это не всегда так.

Различные периодические продолжения сигнала ведут к различным типам ДКП. Ниже приводятся матрицы для первых четырёх типов ДКП:

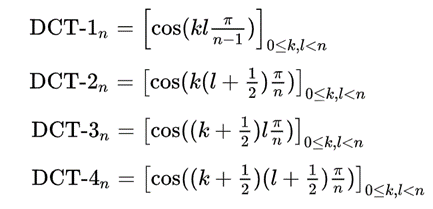
Именно 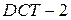чаще всего встречается в практических приложениях благодаря свойству «уплотнения энергии». ДКП для вектора из 8 чисел часто называют . Наиболее распространён двумерный вариант преобразования для матриц 8x8, состоящий из последовательности , начала для каждой строки, а затем для каждого столбца матрицы.

Для расчёта коэффициентов ДКП используется следующее выражение:

где - индексы коэффициента ДКП для смещения на изображении; 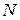- размер окна; 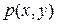- значение интенсивности яркости изображения в пикселе с координатами . Для блока 8х8 получим матрицу коэффициентов T:

На рис. 1 показано, как работает двумерное DCT‑преобразование. Изображение разбивается на блоки 8x8 пикселов. DCT‑преобразование конвертирует блок значений пикселов в набор коэффициентов косинусных функций с возрастающими частотами. Коэффициенты отражают присутствие тех или иных пространственных частот. На иллюстрации показаны блоки пикселов, которые получаются из каждого коэффициента. Верхний левый коэффициент представляет среднюю яркость блока, и, таким образом, является средним арифметическим значением всех пикселов, его также называют DC‑коэффициентом. Справа налево коэффициенты представляют увеличивающуюся горизонтальную пространственную частоту. Сверху вниз коэффициенты представляют увеличивающуюся вертикальную пространственную частоту. Само по себе DCT‑преобразование не производит никакого сжатия информации, то есть не устраняет избыточность. На самом деле полная информация о коэффициентах займет больше места, чем информация об исходных пикселах.

Рис. 1 Принципы дискретного косинусного преобразования

Алгоритм ДКП

Перед началом описания алгоритма, стоит обратить внимание на важное замечание: значения пикселов в полутонового изображения принадлежат интервалу 0..255, так как ДКП работает для значений в интервале -128..127, то требуется произвести сдвиг общего уровня исходного изображения на уровень 128.

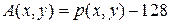
Фрагмент исходного изображения

Фрагмент сдвинутого по уровню -128 изображения

Для вычисления коэффицентов ДКП D воспользуемся соотношением:

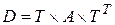
Значения коэффициентов D для заданного фрагмента изображения

Сжатие

Получившиеся значения D далее следует квантовать и сжать. Для этого требуется задать уровень сжатия изображения от 1 до 100, где 100 изображение максимального качества.

Путем множественных экспериментов был подобранные коэффициенты квантования, которые используются в стандартных алгоритмах сжатия JPEG для уровня качества Q50:

Q50 = [

16 11 10 16 24 40 51 61;

12 12 14 19 26 58 60 55;

14 13 16 24 40 57 69 56;

14 17 22 29 51 87 80 62;

18 22 37 56 68 109 103 77;

24 35 55 64 81 104 113 92;

49 64 78 87 103 121 120 101;

72 92 95 98 112 100 103 99

]

Тем не менее если требуется иной уровень качества, то соответствующую матрицу для качества q можно получить из выражения:

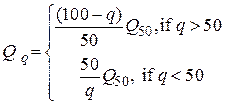
Квантование осуществляется путем деления каждого коэфициентв ДКП на соответствующие значения матрицы квантования и далее округляется до ближайшего целого:

Получившиеся матрица для заданного примера с q = 50

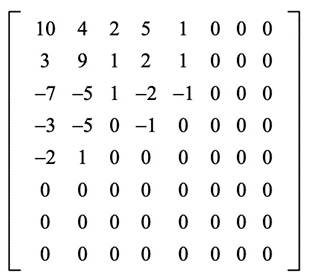
Как видно наибольший вклад вносят низкочастотные составляющие. Высокочастотные гармоники обнуляются. Процедура дальнейшего сжатия предполагает запись получившейся матрицы в виде кода по следующему принципу рис 2.

Рис 2. Последовательность записи кода

Так как последовательность содержит большое количество нулей, то она достаточно хорошо сжимается, например кодом Хэмминга.

Восстановление изображения

Алгоритм восстановления сжатого изображения предполагает повторение всех шагов в обратном порядке:

1. Декодирование кода

2. Получение матрицы

3. Получение изображения

Порядок выполнения работы

1. Ознакомится с теоретической частью. Получить вариант задания;
2. Вывести на экран выбранное изображение;
3. Рассчитать и вывести на экран матрицу коэффициентов ДКП;
4. Рассчитать и вывести на экран матрицу квантованных значений коэффициентов ДКПП;
5. Восстановить и вывести на экран изображение;
6. Полученные изображения представить преподавателю.