Лекция 9. Повторение независимых испытаний
Содержание
1. Схема Бернулли. Формула Бернулли
1.1. Схема независимых испытаний Бернулли
1.2. Формула Бернулли
1.3. Вероятности сложных событий в схеме Бернулли для малого числа испытаний
1.4. Наиболее вероятное число успехов
2. Локальная теорема Муавра-Лапласа
2.1. Вычисление  при больших
при больших 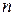 и не малых
и не малых 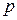
2.2. Свойства и график функции 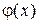
3. Интегральная теорема Муавра-Лапласа
3.1. Вычисление  при больших
при больших 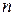
3.2. Свойства и график функции Лапласа 
4. Теорема Пуассона
Схема Бернулли. Формула Бернулли
Схема независимых испытаний Бернулли
Производится серия из 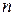 испытаний, удовлетворяющих следующим условиям:
испытаний, удовлетворяющих следующим условиям:
1) каждое испытание имеет два исхода (появление события  - «успех» и появление события «не-
- «успех» и появление события «не-  » =
» =  - «неудача») – взаимно несовместных и противоположных события;
- «неудача») – взаимно несовместных и противоположных события;
2) в каждом испытании вероятность появления события  постоянна и равна
постоянна и равна 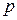 (
( ), тогда вероятность события
), тогда вероятность события  равна
равна  ;
;
3) все 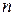 испытаний независимы, т.е. вероятность наступления события в любом из
испытаний независимы, т.е. вероятность наступления события в любом из 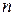 повторных испытаний не зависит от результатов других испытаний.
повторных испытаний не зависит от результатов других испытаний.
Такая схема называется последовательностью испытаний Бернулли, или схемой Бернулли.
Пример 1. Испытания Бернулли:
1) многократное подбрасывание монеты,
2) многократная стрельба по мишени,
3) проверка деталей на годность (для партии, содержащей достаточно большое количество деталей),
4) телефонные звонки по определенному номеру.
Формула Бернулли
Вероятность того, что событие  появится ровно
появится ровно  раз, вычисляется по формуле Бернулли
раз, вычисляется по формуле Бернулли  , где
, где  - биномиальный коэффициент;
- биномиальный коэффициент;  - факториал числа
- факториал числа 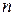 . Считается, что
. Считается, что  . Вероятности
. Вероятности  называются биномиальными.
называются биномиальными.
Пример 2. Произведены четыре независимых выстрела по мишени. Вероятность попадания в мишень при одном выстреле равна 0,6. Найти вероятность того, что мишень будет поражена: 1) три раза; 2) ни разу.
Решение
Последовательность испытаний удовлетворяет всем условиям последовательности повторных независимых испытаний:
§ число испытаний конечно  ;
;
§ каждое испытание заканчивается событием  «попадание в мишень», либо
«попадание в мишень», либо  - «промах»;
- «промах»;
§ вероятность попадания при каждом выстреле  , тогда
, тогда  ;
;
§ все испытания независимы.
1) Применяя формулу Бернулли при  , получим:
, получим:
 .
.
2) Применяя формулу Бернулли при  , получим:
, получим:
 .
.
Вероятности сложных событий в схеме Бернулли для малого числа испытаний
1. Обозначим  - число наступлений события A в последовательности независимых испытаний. События
- число наступлений события A в последовательности независимых испытаний. События  ,
, 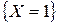 , …,
, …, 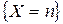 образуют полную группу событий (они попарно независимы и в результате испытаний произойдет только одно из них). Значит, сумма этих событий – достоверное событие. Тогда сумма биномиальных вероятностей
образуют полную группу событий (они попарно независимы и в результате испытаний произойдет только одно из них). Значит, сумма этих событий – достоверное событие. Тогда сумма биномиальных вероятностей 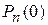 ,
, 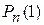 , …,
, …,  , …,
, …,  равна единице
равна единице  .
.
2. Вероятность того, что в последовательности 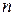 независимых испытаний событие
независимых испытаний событие  наступит:
наступит:
1) менее  раз
раз  ;
;
2) более  раз
раз  ;
;
3) не менее  раз
раз  ;
;
4) не более  раз
раз  ;
;
5) от  до
до  раз
раз  .
.
Пример 3. В условиях примера 2найти вероятность того, что мишень будет поражена от одного до четырех раз.
Здесь  .
.

Пример 4. Найти вероятность того, что в четырех независимых выстрелах мишень будет поражена хотя бы один раз (см. пример 2).
Очевидно, что  как вероятность достоверного события. Отсюда
как вероятность достоверного события. Отсюда  (вероятность
(вероятность  найдена в примере 2).
найдена в примере 2).