РЕЛЯТИВИСТКИЕ ЗАКОНЫДВИЖЕНИЯ МИКРОЧАСТИЦ
(Название лабораторной работы)
1. Цель работы: Знакомство с законами движения микрочастиц, определение их масс и времени жизни.
2. Материалом для работы служат снимки с треками элементарных частиц, полученные в пузырьковой камере. Изображение на снимке уменьшено в два раза.
3. Основные теоретические положения к данной работе:
В данной лабораторной работе изучаются частицы, называемые К-мезоном и Λ-гипероном, которые возникают при столкновении других частиц, π-мезонов, с ядрами некоторых атомов, а затем превращаются снова в π-мезоны и протоны. О некоторых свойствах их можно судить по фотографиям тех следов (треков), которые эти частицы оставляют в специальном приборе для регистрации микрочастиц - пузырьковой камере.
Рабочий объем пузырьковой камеры заполнен жидкостью, находящейся в неустойчивом, перегретом состоянии. Быстро летящая частица ионизирует на своем пути молекулы жидкости, заполняющей камеру. Ионы становятся центрами интенсивного парообразования, и вдоль траектории заряженной частицы появляются пузырьки пара. Образованные этими пузырьками треки фотографируют и исследуют.
Так как, ионизируя молекулы, частица теряет свою энергию иостанавливается, то по длине свободного пробега можно судить о её первона-чальных энергии и импульсе. В данной лабораторной работе связь первоначального импульса p ч частиц с длиной l свободного пробега считается известной и задаётся в виде графика, который имеется в лаборато-рии. Общий вид этого графика приведён на рис.1
Если камеру поместить в магнитное поле, то траек-тория заряженной частицы искривится, так как на такую частицу в магнитном поле действует сила, пер-пендикулярная скорости. По тому, в каком направлении искривится траектория, можно определить знак заряда частицы.
Для получения фотографий, изучаемых в настоящей работе, пузырьковая камера была облучена пучком 
-мезонов (пионов). При столкновении их с ядрами вещества, заполня-ющего камеру, образовались К-мезоны. Они могут быть заряженными (К+- и К--мезоны) или нейтральными (К0-мезоны). Значок справа вверху у символа частицы указывает на знак заряда или его отсутствие. По величине заряд элементарной частицы равен заряду электрона, масса К-мезонов примерно в 1000 раз больше его массы (М ≈ 1000 mе). Продолжительность жизни этих частиц невелика (τ = 10-10 ÷ 10-8 с).
Гипероны являются более тяжелыми частицами. Изучаемый в работе Λ0-гиперон имеет массу примерно в 2200 раз большую массы электрона (М ≈ 2200 mе) и короткое время жизни (τ = 10-10 с).
Так как К-мезоны и Λ0-гиперон живут недолго, то на фотографиях удаётся зафиксировать следы продуктов их распада, по которым можно изучать свойства самих распавшихся частиц. На предлагаемых для изучения при выполнении лабораторной работы фотографиях можно видеть следы одного из следующих превращений:
K0 → π + + π -,
Λ0 → p +π -,
K+ → π + + π + + π -.
Эти превращения схематически изображены на рис. 2.а и рис. З.а. Протон обозначают символом р (знак заряда у протона не ставят, так как он всегда положителен); π -мезоны обозначают символами π + и π -.
Импульс распавшейся частицы в соответствии с законом сохранения импульса равен векторной сумме импульсов частиц - продуктов распада:
Так как импульс принято обозначать той же буквой, что и протон, то в случае импульса мы будем добавлять к ней индекс «ч». Вчастности, выражение для импульса частицы имеющей массу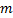 
и скорость 
, в релятивистском случае имеет вид:
,
где с = 3•108 м/с – скорость света в вакуме.
Согласно закону сохранения полная энергия распавшейся частицыравна сумме полных энергий образовавшихся частиц:
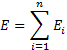
Формулу для энергии запишем в релятивистской форме: 
.
Основываясь на законах сохранения и измеряя длину пробега продуктов распада, можно найти некоторые характеристики распавшихся частиц.
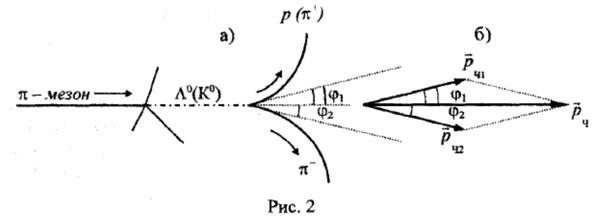Рассмотрим распад нейтральный частицы (К0, Λ0) на две заряженные. На рис. 2.а, изображающем треки частиц в пузырьковой камере, слева дан трек первичного π-мезона (первичный пучок падает слева направо). При столкновении с ядром жидкости, заполняющей пузырьковую камеру, он породил несколько частиц, разлетевшихся в разные стороны («звезда»). Среди них была и нейтральная, которая в пузырьковой камере не оставила следа. На рисунке еетраектория изображена пунктиром. Эта частица короткоживущая, она вскоре распалась на две заряженные частицы, которые оставили в камере след. По длине их пробега можно судить о первоначальных кинетической энергии частиц и импульсе. Так как пузырь-ковая камера находилась в магнитном поле, то треки этих частиц оказались искривленными в противоположные стороны. Обозначим импульс нейтральной частицы р ч, импульсы продуктов ее распада р ч1 и р ч2, углы разлета продуктов распада (φ1 и φ2 (рис. 2.6).
4. Таблицы и графики [1].
I. Изучение распада нейтральных частиц
Таблица 1
| Длина пролёта l о, см | Природа вто- ричных частиц (π+, π-, р) | Углы разлета продуктов распада | Длины пробега продуктов распада, см | Импульсы продуктов распада |
| l о = | φ1 = φ2 = | l1 = l2 = | pч1 = pч2 = |
р ч1 cos φ1 + р ч2 cos φ2 = p ч, (1) 
(3)
р ч1 sin φ1 = р ч2 sin φ2 (2)
Таблица 2
| Частицы | Масса частиц, m, кг | (mс)2, к г2• м 2• с -2 |
Протон( )
Пи-мезон ( )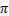
Электрон (e)
| 1,672•10-27 2,50•10-28 9,11•10-31 | 2,516•10-37 5,62•10-39 7,47•10-44 |
Таблица 3
| Импульс, кг • м/с | Масса частицы | Время жизни, с 𝜏=(𝑙/𝑝 ч)𝑀(5) | |
| кг | по отношению к массе электрона | ||
II. Изучение распада К+-мезона
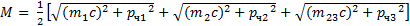(6)
Таблица 4
| Угол вылета π-мезона | Пробег π-мезона, см | Импульс π-мезона, кг м/с | Суммарный импульс, кг • м/с | Масса K +-мезона | |
| кг | по отношению к массе электрона | ||||
| φ1 = φ1 = φ1 = | l 1 = l 2 = l 3 = | pч1 = pч2 = pч3 = |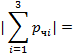 
|
5. Расчёт погрешностей измерений (указать метод расчёта погрешностей).
6. Окончательные результаты:
Подпись студента:
7. Ответы на контрольные вопросы:
1) Рабочий объем пузырьковой камеры заполнен жидкостью, находящейся в неустойчивом, перегретом состоянии. Быстро летящая частица ионизирует на своем пути молекулы жидкости, заполняющей камеру. Ионы становятся центрами интенсивного парообразования, и вдоль траектории заряженной частицы появляются пузырьки пара. Образованные этими пузырьками треки фотографируют и исследуют.
2)
Импульс распавшейся частицы в соответствии с законом сохранения импульса равен векторной сумме импульсов частиц - продуктов распада:
Так как импульс принято обозначать той же буквой, что и протон, то в случае импульса мы будем добавлять к ней индекс «ч». Вчастности, выражение для импульса частицы имеющей массу 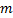и скорость , в релятивистском случае имеет вид:
,
3) Согласно закону сохранения полная энергия распавшейся частицыравна сумме полных энер-гий образовавшихся частиц: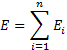
4) Время жизни нейтральной частицы можно определить, измеряя длину ее пролета 1, т.е. расстояния, пройденного частицей от момента её образования до распада. 𝜏=(𝑙/𝑝 ч)𝑀(5)
5) Формула для вычисления времени жизни частицы: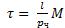 
8. Дополнительная страница (для размещения таблиц, теоретического материала)
Пользуясь законом сохранения импульса и рис. 2.6, получаем: р ч1 cos φ1 + р ч2 cos φ2 = p ч, (1)
р ч1 sin φ1 = р ч2 sin φ2 (2)
В соответствии с законом сохранения энергии и после сокращения на с получаем: 
где М, m1 m2 - массы распавшейся частицы и продуктов распада. По известным импульсам и массам продуктов распада из этих уравнений можно вычислить массу и импульс распавшейся
нейтральной частицы. Время жизни нейтральной частицы можно определить, измеряя длину ее пролета l, т.е. расстояния, пройденного частицей от мо мента её образования до распада. Зная импульс распавшейся ча стицы р ч рассчитаем время ее жизни 
лаб в лабораторной системе отсчета, то есть в системе отсчёта, связанной с лабораторией. Для этого выразим лаб через скорость частицы υ.
(4)
В соответствии с теорией относительности время жизни т в системе отсчета, связанной с частицей (относительно нее частица покоится), является наименьшим и вычисляется по формуле:
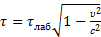
Используя формулу (4), запишем:
.
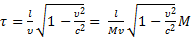Учитывая, что для релятивистского импульса 
в результате получаем: 
По этой формуле можно вычислить время жизни частицы.
Рассмотрим далее распад заряженной частицы К+-мезона (см.рис. 3), которая превращается в три π-мезона. Как это показываютмногочисленные эксперименты, при таком превращении суммарный импульс продуктов распада оказывается близким к нулю. Этозначит, что К+-мезон перед распадом почти останавливается (р ч ≈ 0). Тогда по закону сохранения энергии, зная импульсы и массы продуктов распада, можно определить массу К+-мезона:
(6)