Определение Конечным автоматом Мили называется множество из пяти объектов  , в котором:
, в котором:
 - конечное непустое множество (пространство) состояний,
- конечное непустое множество (пространство) состояний,
 - конечное непустое множество входных сигналов (входной
- конечное непустое множество входных сигналов (входной
алфавит),
 - конечное непустое множество выходных сигналов (выходной
- конечное непустое множество выходных сигналов (выходной
алфавит),
 - функция переходов,
- функция переходов,
 - функция выходов.
- функция выходов.
ЗАМЕЧАНИЕ Автоматы могут задаваться:
1) в виде взвешенного орграфа (диаграмма состояний автомата)
или в виде блок-схемы программы, реализующей поведение
автомата,
2) таблично (функции переходов и выходов задаются в виде таблиц
или совмещенной таблицы состояний).
ЗАМЕЧАНИЕ При графическом изображении автомата состоя
ния обозначают вершинами, а переходы - дугами с направлениями,
определяемыми функцией переходов. При этом над дугой указыва
ются соответствующие значения входа и выхода (взвешенная дуга)
Рассмотрим специальный класс автоматов.
Определение Пусть  . Тогда
. Тогда
функции перехода и выхода  являются функциональными преобразователями. Обозначим их
являются функциональными преобразователями. Обозначим их
соответственно

 ,
,

 ,
,
и реализуем в виде логических схем (ЛС) с  входами и соответст венно
входами и соответст венно  выходами (рис.2.17). Составим из них ЛС, соединив выходы левого блока с соответствующими входами правого и левого
выходами (рис.2.17). Составим из них ЛС, соединив выходы левого блока с соответствующими входами правого и левого
блоков.  входов сделаем общими для обоих блоков. Полученная ЛС (рис.2.18) всегда находится в определенном состоянии, пока на нее не действуют входные сигналы. Ввиду того, что один и тот же сигнал может вызвать разные выходные сигналы, эта ЛС не будет комбинаци онной. Она называется последовательностной схемой или цифровым автоматом.
входов сделаем общими для обоих блоков. Полученная ЛС (рис.2.18) всегда находится в определенном состоянии, пока на нее не действуют входные сигналы. Ввиду того, что один и тот же сигнал может вызвать разные выходные сигналы, эта ЛС не будет комбинаци онной. Она называется последовательностной схемой или цифровым автоматом.
ЗАМЕЧАНИЕ Цифровой автомат задается еще и:
3) аналитически ( задаются в виде функциональных преобразова
задаются в виде функциональных преобразова
телей),
4) в виде логической схемы.
Произвольный автомат можно реализовать как составную часть
цифрового автомата. Для построения последнего нам понадобятся
некоторые понятия.
Определение Пусть  - конечное множество и
- конечное множество и  . Тогда
. Тогда
инъективное отображение  называется кодировщиком
называется кодировщиком
множества  , а сюръективное
, а сюръективное 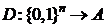 - декодировщиком множества
- декодировщиком множества  .
.
ЗАМЕЧАНИЕ Пусть  - отображение конечного
- отображение конечного
множества  в конечное множество
в конечное множество  и
и  .
.
Тогда это отображение можно представить в виде композиции
 , где
, где  - кодировщик,
- кодировщик,  -
-
функциональный преобразователь и  - декодировщик.
- декодировщик.
Область определения и область значений функционального
преобразователя по числу элементов, вообще говоря, больше
соответственно областей  для отображения
для отображения  .
.
___
Определение Обозначим  алфавит, то есть конечное множе
алфавит, то есть конечное множе
ство элементов (букв),  - множество всевозможных конечных
- множество всевозможных конечных
цепочек букв (слов) вида  . Количество букв в слове называет
. Количество букв в слове называет
ся его длиной и обозначается  . Операция составления двух слов в одно
. Операция составления двух слов в одно  называется склеиванием (сцеплением, конкатена цией) этих слов. Если
называется склеиванием (сцеплением, конкатена цией) этих слов. Если  есть пустая цепочка, то
есть пустая цепочка, то  .
.
Пример  .
.
ЗАМЕЧАНИЕ Множество  представляет собой полугруппу
представляет собой полугруппу
относительно операции склеивания, так как последняя обладает
свойством ассоциативности:  .
.
Понятие склеивания позволяет расширить действие автомата с множества букв  на множество слов
на множество слов  .
.
Определение Расширенными функциями переходов и выходов автомата  называются отображения
называются отображения 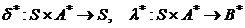 , определяемые рекуррентными формулами:
, определяемые рекуррентными формулами:
 .
.
Следующее замечание дает развернутый алгоритм вычисления значений (представления) расширенных функций на слове.
ЗАМЕЧАНИЕ (свойства расширенных функций)
1)  .
.
2) 

Определение Реакцией состояния  автомата Мили называ ется вход-выходное отображение
автомата Мили называ ется вход-выходное отображение  , определяемое по правилу
, определяемое по правилу  . Реакцией автомата называется совокупность реакций всех состояний этого автомата.
. Реакцией автомата называется совокупность реакций всех состояний этого автомата.
ЗАМЕЧАНИЕ Реакция состояния  совпадает с сужением
совпадает с сужением
расширенной функции выходов  на множество
на множество  .
.
Обратно, совокупность реакций всех состояний определяет
расширенную функцию выходов.
_____
Определение Состояния  автомата
автомата  называются эквива
называются эквива
лентными, если их реакции совпадают:  , то есть
, то есть  .
.
Определение Состояния  автомата
автомата  называются
называются  эквива лентными, если их реакции совпадают на словах длины
эквива лентными, если их реакции совпадают на словах длины  :
:

 .
.
Обозначение  или, что все равно,
или, что все равно, 
ТЕОРЕМА 12.6 1) Множество состояний  разбивается на
разбивается на
максимальные классы  эквивалентных состояний. Совокупность
эквивалентных состояний. Совокупность
таких классов обозначается  .
.
2)  .
.
3) Если  , то
, то  .
.
4) (теорема Хаффмана-Мили)  . То есть, если
. То есть, если
реакции  совпадают на словах длины
совпадают на словах длины  , то
, то
состояния  эквивалентны
эквивалентны
Понятие эквивалентных состояний очевидным образом обобщает
ся на состояния из разных автоматов, у которых одинаковы соответст
венно входные и выходные алфавиты. Это позволяет дать такое
Определение Два автомата с одинаковыми входными и выход ными алфавитами называются эквивалентными автоматами, если каждое состояние одного из них эквивалентно некоторому состоянию другого автомата, и наоборот.
Определение Автомат называется приведенным (минимальным или сокращенным), если все его состояния попарно не эквивалентны.
СЛЕДСТВИЕ Согласно теореме Хаффмана-Мили, начиная с
разбиения  пространства
пространства  все состояния, попавшие в один
все состояния, попавшие в один
класс, имеют одинаковые реакции. Если отождествить все
состояния, попавшие в один класс, то получаем новый автомат,
который является приведенным по построению. Он эквивалентен
исходному автомату, что следует из определения.
АЛГОРИТМ (построения приведенного эквивалентного
автомата). 1) По таблице выходов строим разбиение  .
.
2) По таблице переходов последовательно строим разбиения  ,
,
используя пункт 2) теоремы. В силу пункта 4) таких шагов будет не
более  .
.
3) В силу пункта 3) первое разбиение, для которого  ,
,
определяет классы эквивалентных состояний.
_____
Определение Автомат Мили называется частичным, если функции перехода или выхода определены не всюду. В этом случае в таблице состояний автомата ставят прочерки.
Для формулировки алгоритма построения минимального конечного автомата «покрывающего» произвольный частичный автомат, нам понадобится ряд понятий.
Определение Слово  называется применимым к состоянию
называется применимым к состоянию  , если функция перехода
, если функция перехода  может оказаться неопределенной лишь после считывания последней буквы этого
может оказаться неопределенной лишь после считывания последней буквы этого
слов
Определение Дополним алфавиты  неопределенным симво лом «-». Слово
неопределенным симво лом «-». Слово  покрывает слово
покрывает слово  той же длины, если
той же длины, если  получается из
получается из  заменой некоторых букв
заменой некоторых букв  на прочерк.
на прочерк.  называются совместимыми словами, если существует слово
называются совместимыми словами, если существует слово  , покрывающее и
, покрывающее и  и
и  .
.
Определение Состояния  частичного автомата
частичного автомата  называются совместимыми, если для любого применимого к ним слова
называются совместимыми, если для любого применимого к ним слова  выходные слова совместимы.
выходные слова совместимы.
АЛГОРИТМ (построения всех попарно совместимых состояний)
1) Всевозможные пары состояний изображают в виде клеток. Клетку вычеркивают, если хотя бы для одной буквы 
 . В невычеркнутую клетку
. В невычеркнутую клетку  вписывают все те пара определенных состояний, в которые может перейти
вписывают все те пара определенных состояний, в которые может перейти  .
.
2) Во множестве полученных таким образом невычеркнутых клеток вычеркивают те, в которые вписаны вычеркнутые на первом шаге пары.
3) Шаг 2) повторяется до тех пор, пока будет что вычеркивать. Полученное множество невычеркнутых клеток дает все пары совместимых состояний автомата.
Этот алгоритм имеет наглядный вид при  .
.
Определение Множество попарно совместимых состояний
частичного автомата  называется группой совместимости.
называется группой совместимости.
Определение Конечное число групп совместимости автомата называется группировкой, если любое состояние автомата попадает хотя бы в одну из этих групп.
Определение Группировка называется замкнутой, если для любой группы совместимости  ,
,  либо хотя бы одно из значений
либо хотя бы одно из значений  не определено, либо
не определено, либо  принадлежат одной группе совместимости этой группировки.
принадлежат одной группе совместимости этой группировки.
Пусть автоматы  ,
,  имеют одинаковые входные и выходные алфавиты.
имеют одинаковые входные и выходные алфавиты.
Определение Состояние  автомата
автомата  покрывает состояние
покрывает состояние  автомата
автомата  , если любое слово, применимое к состоянию
, если любое слово, применимое к состоянию  , будет так же применимо к состоянию
, будет так же применимо к состоянию  , а слово
, а слово  покрывает слово
покрывает слово  .
.
Определение Автомат  покрывает автомат
покрывает автомат  , если каждое состояние последнего покрывается некоторым состоянием автомата
, если каждое состояние последнего покрывается некоторым состоянием автомата  .
.
Приведем
АЛГОРИТМ (построения покрывающего автомата)
1) Определяют все пары совместимых состояний.
2) Выписывают все состояния автомата в порядке возрастания
индексов. В этой последовательности вычеркивают все состояния,
несовместимые с первым. Затем вычеркивают все состояния,
несовместимые с первым невычеркнутым. И так далее.
Невычеркнутые состояния составляют первую группу совмести
мости.
Составляют последовательность вычеркнутых состояний. Проде
лывая с ней то же самое, получают вторую группу совместимости.
Получение групп совместимости продолжают, пока есть что
вычеркивать. В результате получается группировка.
3) Если группировка не замкнута, то строят на ее основе замкнутую,
работая с таблицей переходов и оставаясь во множестве пар совме
стимых состояний. При этом либо расширяют группы, совместимо
сти, либо добавляют новые.
4) Группы совместимости полученной замкнутой группировки соста
вляют множество состояний искомого покрывающего автомата. Его
строят, руководствуясь таблицей исходного частичного автомата.
_____
Определение Приведенный автомат Мили называется автоматом с конечной памятью, если существуют такие число  и отображение
и отображение  , что
, что

имеет место равенство  . Наименьшее число
. Наименьшее число  с
с
таким свойством называется памятью автомата.
ЗАМЕЧАНИЕ Если  есть автомат с конечной памятью, то
есть автомат с конечной памятью, то
 будет
будет
 .
.
То есть функционирование автомата вполне определяется знанием предыдущих  входных букв и откликов на них.
входных букв и откликов на них.
ТЕОРЕМА 12.7 1)(Гилл)Если  есть автомат с конечной
есть автомат с конечной
памятью,  , то
, то  .
.
2) Автомат  имеет конечную память тогда и только тогда, когда для
имеет конечную память тогда и только тогда, когда для
некоторого  не существует двух равных вход-выходных путей
не существует двух равных вход-выходных путей
длины  , оканчивающихся в разных состояниях:
, оканчивающихся в разных состояниях:  .
.
Из теоремы следует такой
АЛГОРИТМ (вычисления памяти автомата)
Составим матрицу перехода  автомата.
автомата. 
1)  . Вычисляем
. Вычисляем  , а по ней составляем множества вход-
, а по ней составляем множества вход-
выходных путей длины  :
:  .
.
2) Если  , то полагаем память
, то полагаем память  . В противном
. В противном
случае переходим к 3).
3) Если  , то переходим к 1) и полагаем
, то переходим к 1) и полагаем  . В случае
. В случае
 по теореме Гилла память автомата бесконечна.
по теореме Гилла память автомата бесконечна.
_____
Рассмотрим одну разновидность автоматов Мили.
Определение Автомат Мили  , у которого функция выходов задается в виде
, у которого функция выходов задается в виде  , где
, где  - отображение (называемое определяющим), называется автоматом Мура. То есть функция выходов автомата Мура определяется только состоянием автомата, но не
- отображение (называемое определяющим), называется автоматом Мура. То есть функция выходов автомата Мура определяется только состоянием автомата, но не  , как у автомата Мили, а состоянием
, как у автомата Мили, а состоянием  , в которое он переходит при подаче буквы
, в которое он переходит при подаче буквы  .
.
Обозначение  .
.
Определение Реакцией состояния  автомата Мура называется отображение
автомата Мура называется отображение  , определяемое по правилу
, определяемое по правилу

ЗАМЕЧАНИЕ Каждый автомат Мили порождает эквивалентный ему автомат Мура с числом состояний  по правилу:
по правилу:
каждое состояние исходного автомата заменяется на несколько
состояний в количестве, равном числу различных значений
функции выходов при переходе автомат в это состояние.
_____
Определение Автомат  всегда находится в определенном состоянии
всегда находится в определенном состоянии  . Это состояние называется начальным, а пара
. Это состояние называется начальным, а пара  - инициальным автоматом.
- инициальным автоматом.
ЗАМЕЧАНИЕ Каждый автомат  порождает
порождает 
инициальных автоматов.
Пример (сумматор последовательного действия) Для этого иници ального автомата  ,
,  . На его вход последовательно подаются пары цифр, стоящие в одном разряде слагаемых чисел, начиная с младшего разряда. Значение состояния автомата интерпретируется как "то, что он держит в уме", когда на вход подается пара очередного разряда. При этом функция переходов определяет число, которое автомат будет "держать в уме" в результате сложения цифр этой пары, а функция выходов определяет число, которое он запишет в текущий разряд искомой суммы. Поэтому таблицы функций переходов и выходов
. На его вход последовательно подаются пары цифр, стоящие в одном разряде слагаемых чисел, начиная с младшего разряда. Значение состояния автомата интерпретируется как "то, что он держит в уме", когда на вход подается пара очередного разряда. При этом функция переходов определяет число, которое автомат будет "держать в уме" в результате сложения цифр этой пары, а функция выходов определяет число, которое он запишет в текущий разряд искомой суммы. Поэтому таблицы функций переходов и выходов
 : :
| A \ S |  : :
| A \ S | ||||
| (0,0) | (0,0) | ||||||
| (0,1) | (0,1) | ||||||
| (1,0) | (1,0) | ||||||
| (1,1) | (1,1) |
При сложении, например, двоичных чисел  и
и  берем
берем
последовательно пары одноименных разрядов
 .
.
С помощью таблиц убеждаемся, что сумматор "перерабатывает" это слово побуквенно в слово  .
.
Инициальные автоматы можно охарактеризовать одним
специальным отображением.
Определение Пусть  есть конечные алфавиты. Отображение
есть конечные алфавиты. Отображение  называется автоматным оператором, если оно обладает свойствами:
называется автоматным оператором, если оно обладает свойствами:
1)  ;
;
2) если у слов  совпадают первые
совпадают первые  букв:
букв:  , и
, и  , то
, то  .
.
ЗАМЕЧАНИЕ 1 Автоматный оператор  всегда реализуется в виде некоторого инициального автомата
всегда реализуется в виде некоторого инициального автомата  по правилу
по правилу 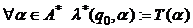 . Обратно, каждый инициальный автомат порождает автоматный оператор по правилу
. Обратно, каждый инициальный автомат порождает автоматный оператор по правилу
 .
.
ЗАМЕЧАНИЕ 2 Если автоматный оператор задан на одном слове  , то с помощью алгоритма покрывающего автомата строится
, то с помощью алгоритма покрывающего автомата строится
приведенный автомат, переводящий слово  в слово
в слово  .
.
Определение Состояние  инициального автомата
инициального автомата  называется достижимым из
называется достижимым из  , если
, если  .
.
СЛЕДСТВИЕ Состояние  не достижимо из
не достижимо из  , если
, если
 .
.
АЛГОРИТМ ( нахождения множества достижимых состояний
инициального автомата)
1) Положим
 .
.
По построению каждое последующее множество содержит предыду
щее.
2) Так как после первого совпадения  все последующие множе
все последующие множе
ства будут совпадать с  и
и  , то первое совпа
, то первое совпа
дение произойдет при  . Поэтому
. Поэтому  есть множество
есть множество
достижимых состояний.
Определение Инициальные автоматы  с
с  ,
,
 называются эквивалентными, если их реакции
называются эквивалентными, если их реакции  совпадают, то есть
совпадают, то есть  .
.
Для формулировки алгоритма эквивалентности инициальных автоматов нам понадобится
Определение Прямым произведением автоматов

называется автомат  , где
, где
 .
.
ЗАМЕЧАНИЕ Достижимость состояния  из
из  в
в
прямом произведении равносильна тому, что
 .
.
ТЕОРЕМА 12.8 (Мура) Инициальные автоматы 
эквивалентны тогда и только тогда, когда для любого достижимого
состояния  инициального автомата
инициального автомата  имеет место равенство
имеет место равенство  .
.
ЗАМЕЧАНИЕ Из определения достижимости следует, что если
из пространства состояний инициального автомата выбросить все
недостижимые состояния, то получится инициальный автомат,
который будет эквивалентен исходному.
_____
Определение Параллельным соединением двух автоматов  с преобразователем информации
с преобразователем информации  называется автомат
называется автомат  , функции которого определяются по правилу
, функции которого определяются по правилу
 ,
,
 .
.
Он имеет следующее схематическое обозначение



Пример Построим по ортогональным конгруэнциям  автомата с таблицей (*) фактор-автоматы
автомата с таблицей (*) фактор-автоматы
 .
.
Образуем их параллельное соединение с функцией переходов
 ,
,
преобразователем информации 
и функцией выходов
 .
.
По условию  . Отсюда
. Отсюда  и
и 
 .
.
В силу последнего равенства полученное параллельное соединение  эквивалентно автомату без выходов (*).
эквивалентно автомату без выходов (*).
Определение Последовательным соединением (суперпозицией) двух автоматов  называется автомат
называется автомат  , функции которого определяются по правилу
, функции которого определяются по правилу  ,
,
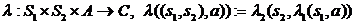 .
.
ЗАМЕЧАНИЕ Параллельное и последовательное соединения
автоматов являются частными случаями каскадной композиции
двух и более автоматов.
Определение Декомпозицией автомата называется представле ние его в виде композиции автоматов с более простой структурой.
Для формулировки алгебраического метода декомпозиции нам понадобится ряд понятий.
Определение Автомат  с таблицей переходов
с таблицей переходов

| 
| 
|
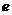
| 
| 
|
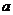
| 
| 
|

| 
| 
|
называется триггером.
ЗАМЕЧАНИЕ Триггер порождает три унарных отображения
пространства состояний:  . Они
. Они
входят во множество всех отображений вида  , и это
, и это
множество замкнуто относительно операции композиции отображе
ний. Оно называется полугруппой триггера. Аналогично строится
полугруппа  для произвольного автомата без
для произвольного автомата без
выходов  . Она называется полугруппой автомата.
. Она называется полугруппой автомата.
Определение Подгруппа  группы называется нормальной, если
группы называется нормальной, если  . Группа
. Группа  называется простой, если у нее нет нетривиальных (=
называется простой, если у нее нет нетривиальных (=  ) нормальных подгрупп.
) нормальных подгрупп.
Определение Автомат  называется автоматом простой группы, если его полугруппа
называется автоматом простой группы, если его полугруппа  является простой группой.
является простой группой.
Определение Группа  делит полугруппу
делит полугруппу  , если существует
, если существует
гомоморфизм  какой-либо полугруппы
какой-либо полугруппы  на
на  :
:  .
.
Имеет место
ТЕОРЕМА 12.9 (о декомпозиции конечного автомата)
1) Две ортогональные конгруэнции  автомата без выходов
автомата без выходов 
порождают параллельное соединения автоматов  ,.
,.
эквивалентное автомату  .
.
2) Одна конгруэнция  автомата без выхода
автомата без выхода  порождают
порождают
эквивалентный  автомат, который является последовательным
автомат, который является последовательным
соединением автоматов.
3) (теорема Крона-Роудза) Конечный автомат можно представить в
виде каскадного соединения из триггеров и автоматов простых
групп, которые делят полугруппу исходного автомата.
ЗАМЕЧАНИЕ Для создания моделей событийно управляемых
систем (- конечных автоматов) и работы с ними в MATLAB есть пакет расширения Stateflow.
____
Преобразование информации есть результат выполнения
некоторого алгоритма, при этом операционный автомат (ОА) реализует содержимое шагов алгоритма, а управляющий автомат (УА) реализует порядок выполнения шагов.
Пример На этом принципе основана работа микрокалькулятора.
ЗАМЕЧАНИЕ При проектировании автомата выделяют три
этапа.
1) Исходной информацией на системном этапе являются совокуп
ность классов решаемых задач и параметры будущего автомата.
Строится композиция пар автоматов ОА и УА. Определяются их
взаимодействие и объемы необходимой памяти.
2) На логическом этапе производится синтез ОА и УА в виде
логических схем. При этом для формализованного синтеза ОА
используется теория бесконечных автоматов, для УА – теория
конечных автоматов. В последнем случае выделяются два этапа:
а) этап построения автоматного оператора (состоит из трех
подэтапов: а1) алгоритмический, а2) абстрактный, а3) кодирование
внутренних состояний) и б) этап структурного синтеза автомата
(реализация его в виде сети или каскадного соединения элементар
ных автоматов).
3) На техническом этапе строится принципиальная монтажная схема
и готовится техническая документация.