· Получите вариант задания у преподавателя.
· Составьте алгоритм поиска элемента по заданному значению.
· Реализуйте алгоритм на языке Си таким образом, программа искала индексы всех имеющихся в массиве заданных элементов.
· Проанализируйте полученные результаты.
Организация поиска подстроки в строке
Цель работы
Ознакомиться и реализовать алгоритмы поиска подстроки в строке.
Последовательный (прямой) поиск
Алгоритм прямого поиска подстроки подобен алгоритму прямого поиска элемента с заданным значением в массиве.
Пусть T – текст, O – подстрока поиска. Длина текста равна m, длина подстроки n.
1. i = 0; // счетчик символов текста
2. ПОКА(i<m)
k = 0; // счетчик совпадений
j=0; // счетчик символов подстроки
i1 = i;
ПОКА(O[j]==T[i1]&& k<n && i1<m)
2.4.1. k++;
2.4.2. j++,i1++;
2.5. Конец цикла
2.6. ЕСЛИ (k==n) ТО вернуть i;// успех при поиске
2.7. i++;
3. Конец цикла
4. Вернуть -1. // неуспех при поиске
В худшем случае, время поиска в этом алгоритме прямо пропорционально n*(m-1).
Алгоритм поиска Кнута
Алгоритм, предложенный Кнутом для осуществления поиска, основан на анализе символов подстроки. В зависимости от вида подстроки и количества имеющихся совпадений алгоритм позволяет выполнить сдвиг по тексту более чем на один символ.
Вся основная работа проводится в начале алгоритма. Если в поиске участвует подстрока длины n, то может быть 0, 1, 2, 3, …, n-1 совпадений с текстом (как только произойдет n совпадений - подстрока найдена). Обозначим за j количество совпадений. Для дальнейшей работы рассчитаем элементы массива  по следующему правилу:
по следующему правилу:
 длина максимальной подстроки до символа с номером j, полностью совпадающей с началом образа.
длина максимальной подстроки до символа с номером j, полностью совпадающей с началом образа.
Значения 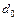 и
и 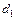 постоянны и равны соответственно -1 и 0.
постоянны и равны соответственно -1 и 0.
Сам сдвиг рассчитывается по формуле: 
Рассмотрим на примере подстроки ААBCDAABD.

| |

| |

| ААBCDAABD |

| ААBCDAABD |

| ААBCDAABD |

| ААBCDAABD |

| ААBCDAABD |

| ААBCDAABD |

| ААBCDAABD |
Предположим, что необходимо найти эту подстроку в тексте
| A | A | B | D | A | A | B | C | A | A | B | C | D | A | A | B | D |
| A | A | B | C | D | A | A | B | D | j=3, shift = 2 | |||||||
| A | A | B | C | D | A | A | B | D | j=0, shift = 1 | |||||||
| A | A | B | C | D | A | A | B | D | j=0, shift = 1 | |||||||
| A | A | B | C | D | A | A | B | D | j=4, shift = 3 | |||||||
| j=9, поиск окончен | A | A | B | C | D | A | A | B | D |
Поиск Боуера-Мура
Этот поиск начинает сравнивать подстроку со строкой, начиная с последнего символа подстроки. Пусть сравнение начинается с позиции i -1. Если нет полного совпадения, то сдвиг можно произвести на величину  , где
, где  - символ строки в позиции i-1. Сама величина сдвига определяется следующим образом:
- символ строки в позиции i-1. Сама величина сдвига определяется следующим образом:
- d равно длине образа, если символ не принадлежит подстроке;
- d равно расстоянию от самого правого в подстроке вхождения символа до ее конца.
Рассмотрим на примере подстроки «образ », подстрока ищется в тексте «отказ приказ город образ пример ». Аналогично поиску Кнута таблица сдвигов рассчитывается еще до работы алгоритма и для рассматриваемого примера равна:

| 
| 
| 
| 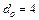
|
Все остальные символы алфавита имеют d равное 5 (длине образа).
| о | т | к | а | з | п | р | и | к | а | з | г | о | р | о | д | … | ||
| о | б | р | а | з | сдвиг на 5 позиций | |||||||||||||
| о | б | р | а | з | сдвиг на 5 позиций | |||||||||||||
| о | б | р | а | з | сдвиг на 4 поз. | |||||||||||||
| о | б | р | а | з |
| г | о | р | о | д | о | б | р | а | з | п | р | и | м | е | р | ||||
| о | б | р | а | з | сдвиг на 5 позиций | ||||||||||||||
| о | б | р | а | з | подстрока найдена |