Тема 10. Применение свойств функции при решении задач
Некоторые свойства функций, которые могут быть применены при решении задач:
- ограничения на область значений;
- монотонность;
- четность (как следствие – симметрия графиков и решений)
Кроме того, конечно, необходимо уметь работать с функциями, заданными в общем виде, в том числе с композициями функций (т.е. с так называемыми сложными функциями).
Ограничения на область значений функции
Задачи, в которых применяется идея на ограничения по области значения функций, можно условно разделить на два вида:
1) задачи, где нужно найти максимум или минимум какой-либо функции (или, если это задача с параметром, например, нужно найти значения параметра, при которых будет достигаться определенное значение экстремума);
2) задачи на так называемый метод мажорант. Мажорантой функции 
на множестве А называется такое число М, что либо 
для всех 
, либо 
для всех .
Пусть дано уравнение 
и существует такое число М, что для любого х из области определения и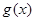 
получаем и 
. Тогда уравнение эквивалентно системе 
.
В некоторых случаях может быть дана задача, где можно сравнить заданные функции с третьей, график которой проходит между ними.
Пример 1
Решить уравнение 
.
Монотонное возрастание (убывание) функции
Функция называется возрастающей на промежутке D, если для любых чисел 
и 
из промежутка D таких, что 
, выполняется неравенство 
.
Функция называется убывающей на промежутке D, если для любых чисел и из промежутка D таких, что , выполняется неравенство 
.
Если функция возрастает или убывает на некотором промежутке, то она называется строго монотонной на этом промежутке. Если функция не возрастает или не убывает на некотором промежутке, то она называется монотонной на этом промежутке
Заметим, что если – монотонная функция на промежутке 
, то уравнение 
не может иметь более одного корня на этом промежутке.
Свойства монотонных функций
(предполагается, что все функции определены на некотором промежутке D):
- Сумма нескольких возрастающих функций является возрастающей функцией;
- Произведение неотрицательных возрастающих функций есть возрастающая функция;
- Если функция возрастает и дана некоторая константа с, то функции
, где (c > 0), и 
также возрастают, а функция , где
(c < 0), убывает; - Если функция возрастает и сохраняет знак, то функция
убывает; - Если функция возрастает и неотрицательна, то
, где n є N, также возрастает; - Если функция возрастает и n – нечетное число, то также возрастает;
- Композиция
возрастающих функций и 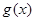также возрастает.
Аналогичные утверждения можно сформулировать и для убывающей функции.
Использование монотонности функций при решении уравнений и неравенств основано на следующих теоретических фактах:
- Строго монотонная функция принимает каждое свое значение ровно один раз, следовательно, если дана строго монотонная функция и
, то 
; - Если одна функция возрастает, а другая убывает на одном и том же промежутке, то графики их либо только один раз пересекутся, либо вообще не пересекутся, а это означает, что уравнение
имеет не более одного решения; - Если на некотором промежутке одна из функций убывает (возрастает), а другая принимает постоянные значения, то уравнение либо имеет единственный корень, либо не имеет корней;
Таким образом, при этом способе исследуются на монотонность левая и правая части уравнения, и если оказывается, что функции удовлетворяют какому-либо из приведенных условий, то найденное подбором решение будет единственным корнем уравнения.
Пример 2
Решить уравнение 
.
Симметрия
Важно в задачах обращать внимание на четность функций, а также на другие ситуации, когда в уравнении или в системе наблюдается симметрия, так как если уравнение обладает некоторой симметрией, то такой же симметрией обладают и все его решения.
Это означает, что не решая уравнение и исходя лишь из соображений симметрии, мы можем заранее предвидеть некоторые свойства его решений.
Пример 3
При каких значениях параметра а система 
имеет единственное решение?
Семинар 10
Декабря 2018
1. Пусть f, g, h – функции, определенные на x>0, такие что f (g (x))= g (h (x)).
Если f (x)= x +1, 
, то чему равна h (x)?
2. При каких значениях параметров a и b система 
имеет единственное решение?
3. Решить уравнение 
.
4. При каком значении параметра а наибольшее на промежутке 0 ≤ х ≤ 1 значение функции 
является наименьшим?
5. Задана функция f, причем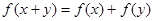 
для всех рациональных чисел х, у. Известно, что 
. Найти 
.
Домашнее задание 10
Декабря 2018
1. При каких значениях параметра а уравнение 
имеет хотя бы одно решение?
2. Решить уравнение: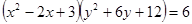 
.
3. Найти все а, при которых минимум функции 
больше единицы.
4. Пусть f и g функции, определенные на всей числовой оси, такие, что 
и 
. Найдите такое значение х, при котором 
.
5. Найти все значения параметра a, при которых система 
имеет единственное решение.
6. Решить уравнение 
.
7. Функция 
определена на отрезке [5; 7].При каких значениях параметра а наибольшее на этом отрезке значение функции f (x) не превышает 
?
8. При каких значениях параметра а уравнение 
имеет на полуинтервале (-1; 1] ровно три корня?
9. При каких значениях параметра а наименьшее на промежутке 
значение квадратного трехчлена 
равно 3?
10. При каких значениях параметра а неравенство 
справедливо для любых пар (x; y), для которых | x | = | y |?