Равносторонний треугольник
Радиус описанной около равностороннего треугольника окружности определяется по формуле:
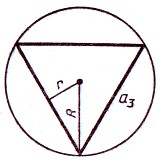
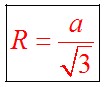
Радиус вписанной в равносторонний треугольник окружности определяется по формуле:
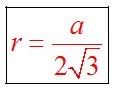
Прямоугольный треугольник
Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы.
Радиус описанной около прямоугольного треугольника окружности равен длине медианы, проведенной к гипотенузе.
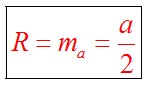
Радиус вписанной в прямоугольный треугольник окружности определяется по формуле:
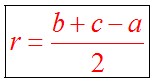
В многоугольнике
· Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех внутренних углов данного многоугольника пересекаются в одной точке, которая и является центром вписанной окружности.
· Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру
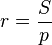
В треугольнике
Свойства вписанной окружности:
· В каждый треугольник можно вписать окружность, притом только одну.
· Центр I вписанной окружности называется инцентром, он равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.
· Радиус вписанной в треугольник окружности равен
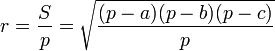
где S — площадь треугольника, а p — полупериметр.
· Если AB — основание равнобедренного 
, то окружность, касающаяся сторон 
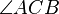в точках A и B, проходит через инцентр треугольника ABC.
· Формула Эйлера: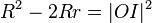 
, где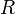 
— радиус описанной вокруг треугольника окружности, 
— радиус вписанной в него окружности, O — центр описанной окружности, I — центр вписанной окружности.
· Если прямая, проходящая через точку I параллельно стороне AB, пересекает стороны BC и CA в точках A1 и B1, то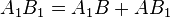 
.
· Точки касания вписанной в треугольник T окружности соединены отрезками — получается треугольник T1
· биссектрисы T являются серединными перпендикулярами T1
· Пусть T2 — ортотреугольник T1. Тогда его стороны параллельны сторонам исходного треугольника T.
· Пусть T3 — серединный треугольник T1. Тогда биссектрисы T являются высотами T3.
· Пусть T4 — ортотреугольник T3, тогда биссектрисы T являются биссектрисами T4.
· Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен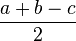 
.
· Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно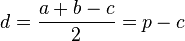 
.
· Расстояние от вершины C до центра вписанной окружности равно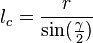 
, где r — радиус вписаной окружности, а γ — угол вершины C.
· Расстояние от вершины C до центра вписанной окружности может также быть найдено по формулам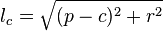 
и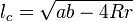 
· Теорема о трезубце или о трилистнике: Если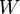 
— точка пересечения биссектрисы угла 
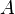с описанной окружностью, а 
— центр вписанной окружности, то 
.
· Лемма Веррьера[1]: пусть окружность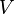 
касается сторон 
, 
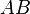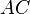и дуги 
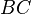описанной окружности треугольника 
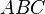. Тогда точки касания окружности 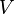со сторонами и центр вписанной окружности треугольника 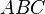лежат на одной прямой.
В четырёхугольнике
Описанный четырёхугольник, если у него нет самопересечений («простой»), должен быть выпуклым.
В выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны: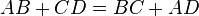 
.
Во всяком описанном четырёхугольнике середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона). На ней же лежит середина отрезка с концами в точках пересечения противоположных сторон четырёхугольника. Эта прямая называется прямой Гаусса. Центр описанной около четырёхугольника окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара).
В сферическом треугольнике
Вписанная окружность для сферического треугольника — это окружность, касающаяся всех его сторон.
· Тангенс радиуса[2] вписанной в сферический треугольник окружности равен[3]:73-74
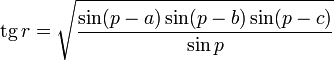
· Вписанная в сферический треугольник окружность принадлежит сфере. Радиус, проведенный из центра сферы через центр вписанной окружности пересечет сферу в точке пересечения биссектрис углов (дуг больших кругов сферы, делящих углы пополам) сферического треугольника[3]:20-21.