ЭВМ выполняет действия поочередно (складывает пару чисел) и округляет результат после каждого действия.

АЛГОРИТМЫ

ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ

КУРС ЛЕКЦИЙ

 

Автор: доцент кафедры ВТИК УГНТУ Мухамадеев И.Г.

Текст подготовил: ст. гр. ТЭ-03
Валишин А.Р.

 

 

УФА 2007

 

Литература по вычислительной математике

 

Основная литература:

 

1. Боглаев Ю.П. Вычислительная математика и программирование. – М.: Высшая школа, 1990.

2. Демидович Б.П., Марон Н.А. Основы вычислительной математики. - М.: Наука, 1970. – 660 с.

3. Гловацкая А.П. Методы и алгоритмы вычислительной математики. - М.: Радио и связь, 1999. - 408 с.

4. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании. – М.: Финансы и статистика, 1999.

5. Потёмкин В.Г. Система MATLAB. Спр. пособие. – М.: Диалог - МИФИ. 1998 – 350 с.

6. Умергалин Т.Г. Основы вычислительной математики: Учебное Пособие. - Уфа, Изд-во УГНТУ, 2003. – 106 с.

7. Джонсон К. Численные методы в химии. – М.: Мир,1983. – 504 с.

8. Шуп Т.Е. Прикладные численные методы в физике и технике. - М:. Высш. Шк., 1990.

9. Очков В.Ф. MathCAD 7.0 Pro для студентов и инженеров. М:. Компьютер-Пресс, 1998. = 384 с.

10. Дьяконов В.П. Справочник по применению системы EUREKA.-М.: Физматлит, 1993.-96 с.

 

Учебные пособия:

 

1. Мухамадеев И.Г. Решение систем нелинейных уравнений. /Мет. указания/. – УНИ, Уфа. – 1988 г. (7 / 11)

2. Кирлан Л.Д. Приближенные методы решения дифференциальных уравнений и их систем на мини- и микро-ЭВМ. /Мет. указания/. – УНИ, Уфа. -1987 г.

3. Калиновский Ю.В., Мухамадеев И.Г. Решение алгебраических и трансцендентных уравнений. /Мет. указания/. – УНИ, Уфа – 1987 г.
(7 / 6).

4. Калиновский Ю. Кайбышева Д.А. Мухамадеев И.Г. Численное интегрирование /Мет. указания/. – УНИ, Уфа, 1988

5. Иванов В.И., Лизунов А.Н., Мухамадеев И.Г.Аппроксимация функций /Мет. указания/. - Уфа, Изд. Уфим. нефт. института, 1989.

Тема 1

Введение.

 

В настоящее время в науке и инженерной практике широко используется метод математического моделирования.

 

Математическим моделированием [1]называется изучение реального объекта на ЭВМ с помощью математической модели этого объекта.

 

 

Например:

1. Совершенствование ядерного оружия путем расчетов на супер-ЭВМ. Удалось отказаться от испытаний ядерного вооружения.

2. Компьютерные тренажеры (симуляторы), созданные на основе математических моделей, появились сначала у военных, сейчас они широко применяются в производственном и учебном процессе.

 

Математическая модель – это приближенное математическое описание объекта (технологического процесса, реакции, явления и т.д.).

Примеры простейших моделей:

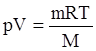уравнение состояния идеального газа (1.1)

F = 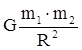закон всемирного тяготения (1.2)

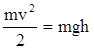закон сохранения энергии (1.3)

закон Кулона (1.4)

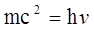закон сохранения энергии для фотона, (1.5)
где v – частота излучения.

Сложные модели описывают объект точнее (адекватнее [2] ).

Математическое моделирование позволило исследовать на ЭВМ очень сложные процессы, такие, например, как глобальные климатические изменения в результате применения ядерного оружия (натурный эксперимент имеет катастрофические последствия).

В литературе математическое моделирование часто принято называть вычислительным экспериментом.

 

Основные этапы математического моделирования:

1. Разработка модели – формализация. Изучается в прикладных и фундаментальных науках.

2. Разработка метода (алгоритма) решения уравнения модели – алгоритмизация. Изучается в вычислительной математике.

3. Создание программы – программирование. Изучается в информатике.

4. Расчеты, анализ результатов – практическое использование.

	Использование результатов:

Результат

	Расчёты

 

 

Программа

 

для совершенствования

Алгоритм

		алгоритма

 

для совершенствования

Мат. модель

 

 

проектирования

Объект

 

Предметом вычислительной математики являются численные методы (алгоритмы) решения математических задач, возникающих при исследовании реальных объектов методом математического моделирования.

 

Например, пусть нужно найти R из уравнения (1.2) или (1.4), из уравнения (1.3) или c из уравнения (1.5). Что общего в этих задачах? То, что нужно решить уравнение вида:

x ² = a (1.6)

Вычислительная математика не рассматривает решения конкретных задач (1.2÷1.5), а изучает их решение в общем, абстрактном виде (1.6).

С точки зрения обычной математики точное решение уравнения (1.6) имеет вид:

= ,

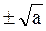причем если a > 0, то два вещественных решения;

если а = 0, то тривиальное решение ;

если а < 0, то вещественных решений нет.

 

Но знак не решает задачу, так как не дает практического способа (алгоритма) вычисления значения х для конкретного значения а.

Вычислительная математика предлагает следующий алгоритм вычисления x*:

1. Выбрать начальное значение х, например =а. Это начальное приближение решения.

2. Вычислять новые приближения решения x_i по формуле:

x_i = (1.7)

до достижения условия:

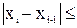e (1.8)

Здесь i = 1,2,.. – номер вычисления - итерации.

e – требуемая точность.

Пример. Нужно решить уравнение 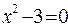с точностью e=0,001.

Зададимся ,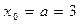

Вычислим первое приближение: ,

оценим точность | x₁ – x₀ | = 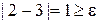.Требуемая точность не достигнута, нужно продолжить расчет.

Вычислим второе приближение: ,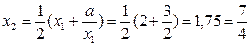

оценим точность .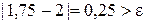

Вычислим третье приближение: ,

оценим точность .

Вычислим четвертое приближение: ,

оценим точность − точность достигнута.

Ответ: .

Точное значение (до 8 значащих цифр):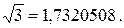

Рассмотренный пример демонстрирует принципы, общие для итерационных методов решения задач вычислительной математики:

1. Исходная задача (1.6) заменяется другой задачей – вычислительным алгоритмом по формулам (1.7), (1.8), где используются только арифметические операции + 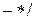. Принято называть (1.7) формулой итерационного процесса (итерационным процессом), (1.8) - условием завершения итерационного процесса.

2. Задача (1.7) содержит новый параметр i – номер итерации. Очевидно, что число итераций влияет на точность решения.
Если 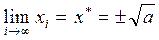, то итерационный процесс является сходящимся – позволяет получить решение исходной задачи (1.6).

3. Решение, полученное итерационным методом, всегда является приближенным, так как точное решение получить невозможно – нужны бесконечные вычисления.

Важно подчеркнуть, что формула (1.7) получена из (1.6) путём тождественных преобразований:

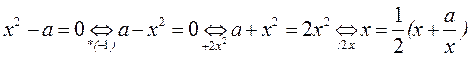
Но не всякое тождественное преобразование позволяет получить сходящийся итерационный процесс.

Например:

a)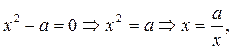

Выполним расчет при а=3:

; ; ;

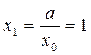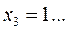
Итерационный процесс не сходится; значения приближений колеблются.

б)

; …

Итерационный процесс расходится.

Рассмотренный пример иллюстрирует один из видов численных методов – итерационный.

Виды численных методов:

1. Прямые – решение получают за конечное число арифметических действий.

2. Итерационные – точное решение может быть получено теоретически в виде предела бесконечной сходящейся последовательности вычислений.

3. Вероятностные – методы случайного поиска решения (угадывания).

 

Все виды численных методов позволяют получить только приближенное решение задачи, то есть численное решение всегда содержит погрешность.

Тема 2

Структура погрешности численного решения задачи.

Точность решения задачи оценивается абсолютной или относительной погрешностью.

Абсолютная погрешность:

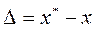, (2.1)

где - точное решение,

x - численное решение.

Относительная погрешность:

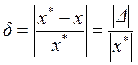, (2.2)

Источники погрешности численного решения задачи:

1. Погрешность математической модели.

Возникает в результате допущений, принятых при получении модели. Реальность всегда сложнее любой модели, поэтому этот источник погрешности всегда влияет на численное решение. Величина этой погрешности определяется сравнением экспериментальных данных с результатами расчетов по модели (оценивается адекватность модели объекту).

 

2. Погрешность исходных данных.
Зависит от точности измерения параметров, используемых в модели. Любые измерения приближенны, поэтому и этот источник всегда влияет на решение.

В вычислительной математике эти два вида погрешности (погрешность математической модели и погрешность исходных данных) принято называть неустранимой погрешностью, т.к. она не зависит от метода решения задачи и всегда влияет на ее решение, и ее обязательно нужно учитывать при анализе полученного решения.

 

3. Погрешность метода решения задачи.
Возникает в результате применения итерационного или вероятностного метода решения.
Эти методы позволяют получить точное решение только в результате бесконечной последовательности действий. Поэтому для получения приближенного решения бесконечный процесс прерывают при достижении требуемой точности решения.

 

4. Погрешность округления .
Возникает в результате проведения вычислений с конечным числом значащих цифр.

Погрешность элементарных арифметических действий изучается в теории погрешности. Учесть погрешность округления при большом количестве арифметических действий практически невозможно.

Есть случайные и систематические источники погрешности округления.

Случайные источники обычно компенсируют друг друга.

Например:

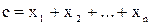
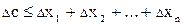
Знаки случайны и компенсируют друг друга при большом n.

Систематические источники вызывают накопление погрешности округления. Они являются дефектом структуры вычислений (алгоритма).

Пример 2.1

Требуется вычислить:

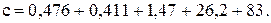
Сложим эти числа столбиком и, округлив результат до 3-х значащих цифр, получим значение с:

0,476

0,411

1,47

26,2

83,

111,557 » 112.

 

ЭВМ выполняет действия поочередно (складывает пару чисел) и округляет результат после каждого действия.

Выполним суммирование слева направо в порядке записи (как ЭВМ):

+ 0,476 + 0,887 + 2,36 + 28,6

0,411 1,47 26,2 83,

0,887 »0,887 2,357»2,36 28,56 »28,6 111,6 » 112.

Пусть теперь выражение записано в обратном порядке:

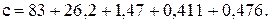
Выполним суммирование как ЭВМ:

+ 83 + 109 +110 + 110

26,2 1,47 0,411 0,476

109,2 »109 110,47 »110 110,411 »110 110,476 » 110

От перестановки слагаемых сумма изменилась, то есть

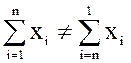
Пример 2.2

Требуется перемножить 100 чисел, причем первая половина из них равна 0,1, вторая 10 (числа упорядочены по возрастанию значений).

Если в программе на языке Pascal последовательно перемножать числа, начиная с первого, то результат будет равен 0 (самое маленькое по модулю значение переменной типа Real на языке Pascal ± 2,9 ·10^-39 ).

Если же последовательно перемножать с конца, то произойдет переполнение (самое большее по модулю значение переменной типа Real на языке Pascal 1,7·10 ³⁸ ).

Если же эти значения чередуются, то независимо от порядка умножения результат будет равен 1,0.

Следовательно, от перестановки мест сомножителей значение произведения в рассмотренном случае меняется.

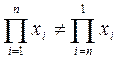
В машинной арифметике законы коммутативности ( переместительный ) и дистрибутивности ( распределительный ) не всегда соблюдаются.

Рекомендации для снижения ошибок округления:

1. При сложении и вычитании последовательности чисел действия необходимо начинать с наименьших по абсолютной величине значений.

2. Следует избегать вычитания двух близких чисел, преобразуя выражения.

3. Количество арифметических действий для решения задачи нужно сводить к минимуму.

4. Для уменьшения ошибки округления расчеты следует проводить с повышенной разрядностью (doubleprecisionв Pascal).

При выборе численного метода решения задачи необходимо учитывать следующее:

1. Погрешность метода должна быть на порядок меньше неустранимой погрешности. Увеличение погрешности метода снижает точность, уменьшение – увеличивает время решения задачи.

2. Погрешность округления должна быть значительно меньше (на два порядка) погрешности метода и неустранимой погрешности.

Для оценки погрешности решения на практике можно использовать следующие приемы:

1. Решить задачу различными численными методами и результаты сравнить.

2. Незначительно изменить исходные данные и повторно решить задачу. Результаты сравнить. Если они различаются сильно, задача или метод ее решения являются неустойчивым – выбрать другой.

 

Тема 3

Численное решение алгебраических и трансцендентных урав нений.

 

Решение уравнений – это одна из древнейших математических задач. Ещё в Древней Греции умели решать линейные и квадратные алгебраические уравнения. В эпоху Возрождения (XV век) Джироламо Кардано и его ученик Луиджи Феррари получили точные решения для алгебраических многочленов 3 и 4 степени. Позднее много усилий было затрачено на получение точного решения многочленов 5 степени и выше. Но только в 20-х годах XIX века было доказано, что решение алгебраического многочлена n-ой степени

a_n x ⁿ + a_n-1x^n-1 +...+ a₀ = 0, где a_n ¹ 0

при n ³ 5 нельзя выразить через коэффициенты с помощью арифметических действий и операций извлечения корня.

Известно, что алгебраический многочлен n-ой степени имеет n корней, причём они могут быть вещественными и комплексными (теорема Гаусса).

Решение трансцендентных уравнений в явном виде также может быть получено в редких, простейших случаях. Трансцендентные уравнения, включающие алгебраические, тригонометрические, экспоненциальные функции от неизвестного x, как правило, имеют неопределённое число корней. Необходимость решения трансцендентных уравнений возникает, например, при расчёте устойчивости систем, расчете парожидкостного равновесия и т.п.

Достаточно распространенной задачей является так же нахождение некоторых или всех решений системы из n нелинейных алгебраических или трансцендентных уравнений с n неизвестными.

Рассмотрим вначале методы решения нелинейных уравнений с одним неизвестным.

Пусть задана непрерывная функция f(x) и требуется найти корни уравнения

f(x)=0 (3.1)

на всей числовой оси или на некотором интервале .

Всякое значение 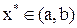, удовлетворяющее условию 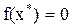, называется корнем уравнения (6.1), а способ нахождения этого значения 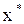и есть решение уравнения (3.1).

Методы решения уравнений:

· Прямые (формула Виета для квадратного уравнения и Кардано для кубического и другие)

· Итерационные – для решения любого уравнения

Численное решение уравнения проводится в два этапа:

1 этап. Отделение корней уравнения.

2 этап. Уточнение интересующих корней с заданной точностью ε.

 

3.1. Отделение корней нелинейного уравнения.

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a,b], которому он принадлежит.

На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.

В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается аналитическими и графическими методами.

Аналитические методы основаны на функциональном анализе.

Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида

P_n(x) = a_n x ⁿ + a_n-1x^n-1 +...+a₁x+ a₀ = 0, (a_n >0) (3.2)

верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):

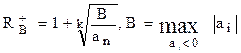, (3.3)

где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;

B – максимальный по модулю отрицательный коэффициент.

Нижнюю границу положительных действительных корней 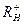можно определить из вспомогательного уравнения

(3.4)

Если для этого уравнения по формуле Лагранжа верхняя граница равна R₁, то

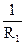= (3.5)

Тогда все положительные корни многочлена лежат в интервале

≤x⁺≤ .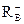

Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.

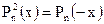и .

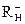≤x^–≤ = = .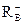

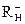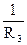
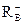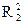Рассмотрим пример отделения корней с использованием этого аналитического метода.

Методом Лагранжа определим границы положительных и отрицательных корней многочлена.

3x⁸ – 5x⁷ – 6x³ – x – 9 = 0

k = 1 B = |– 9| a_n = 3

= 4

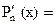9x⁸ + x⁷ + 6x⁵ + 5x – 3 = 0

k = 8 B = 3 a_n = 9

Отсюда границы положительных корней 0,5 ≤ x⁺ ≤ 4

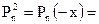3x⁸ + 5x⁷ + 6x³ + x – 9 = 0

=

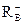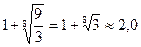
9x⁸ – x⁷ – 6x⁵ – 5x – 3 = 0

k = 1 B = 6 a_n = 9

Следовательно, границы отрицательных корней –2 ≤ x^– ≤ –0,6

Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.

Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.

На практике получил большее распространение графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.

На графике 3 корня. Первый корень x * Î [a,b]

b x2* x3*

x

x1*

a

y=f(x)

y

Рис. 3.1 Отделение корней на графике f(x).

y=f(x)

2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

		На графике 2 корня. Первый корень x 1* Î [a,b]

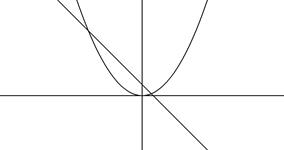
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

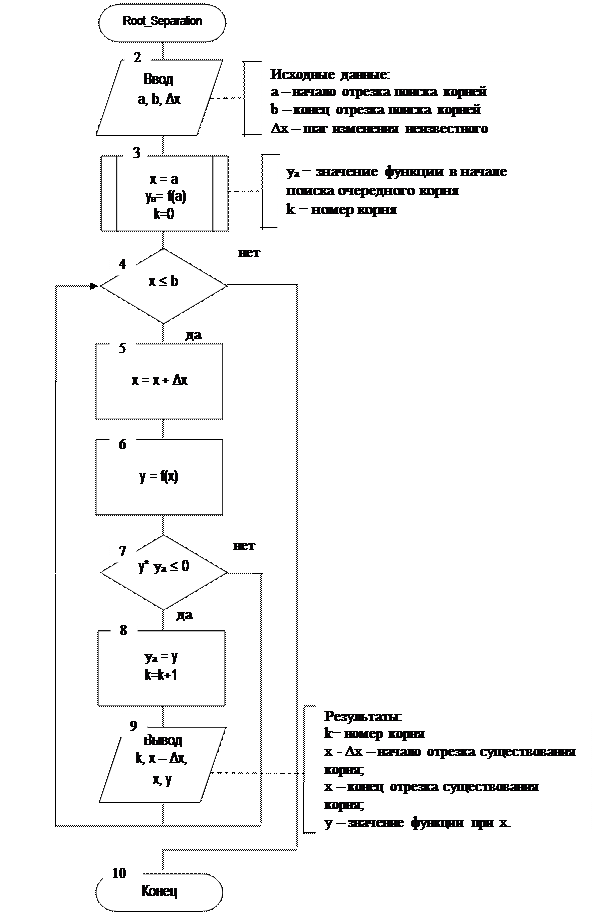Рис. 3.3 Схема алгоритма отделения корней.

3.2. Алгоритмы уточнения корней уравнения.

Уточнение корня – это вычисление интересующего корня с заданной точностью e.

Приближённые значения корней уравнения, полученные на предыдущем этапе, уточняются различными итерационными методами.

Рассмотрим некоторые из них.

 

3.2.1. Метод дихотомии (половинного деления, бисекций).

Постановка задачи:

Дано нелинейное уравнение ¦(x) = 0.

Корень отделен, т.е. известно, что x^* Î [a,b].

Требуется вычислить корень с заданной точностью ε.

Метод реализует стратегию постепенного уменьшения отрезка существования корня, используя факт изменения знака функции в окрестности корня.

Алгоритм метода.

1. Вычислить координату середины отрезка [a,b] x = (a+b)/2 и значение ¦(x) в этой точке.

2. Уменьшить отрезок, отбросив ту его половину, на которой корня нет.

Если знак функции в начале отрезка и в его середине одинаков, то корень находится на второй половине, первую половину можно отбросить, переместив начало отрезка в его середину:

если ¦(a) ·¦(x)>0 => x^*Î [x,b] => a=x, иначе x^*Î [a, x] => b=x

3. Проверить условие завершения вычислений: длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью:

b-a ≤ ε ∩ |¦(x)| ≤ ε.

Если условие достигнуто, расчет завершен, иначе повторить алгоритм сначала.

 

 

x

/

/

a

 

/

/

 

 

Рис. 3.4 Геометрическая иллюстрация метода бисекций.

 

 

 

b=x

 

 

Рис. 3.5 Схема алгоритма метода бисекций (дихотомии)

 

Количество итераций n, требуемых для достижения требуемой точности ε можно оценить заранее из соотношения

(3.6)

Метод дитохомии − простой и надежный метод поиска простого корня любой функции, устойчивый к погрешности округления. Даже если на отрезке есть несколько корней (нечетное количество),то будет найден один из них.

Недостатки метода: скорость сходимости низкая, не обобщается на систему уравнений.

Метод дихотомии нельзя использовать для уточнения не простого корня − корень совпадает с точкой экстремума функции, т.к. в этом случае функция не изменяет свой знак в окрестности корня.

 

Рис. 3.6. Непростой корень уравнения.

Пример 3.1. Требуется решить уравнение x³+2x=1

Сначала нужно отделить решения.

Удобно записать уравнение в виде x³=1-2x и построить графики двух элементарных функций ¦1(x)= x³ и ¦2(x)=1-2x

 

Рис. 3.7 Отделение корней уравнения x³ = 1 - 2 x.

Из графика следует, что корень один: x^* Î [0;1].

Проверим наличие корня на отрезке

¦(a) = ¦(0) = 0³+2·0 = -1, ¦(b) = ¦(1) = 1³+2·1 = 2

Знаки на концах отрезка разные, следовательно, корень отделен верно.

Выполним несколько итераций уточнения корня.

1 итерация. Середина отрезка x = (0 + 1) / 2 = 0,5

Значение функции в середине ¦(x)=¦(0,5)= 0,53+2·0,5-1=0,125>0

Функция меняет свой знак на первой половине отрезка, следовательно, корень на первой половине, поэтому отбросим вторую половину, переместив конец отрезка в середину: x* Î [0;0,5]

2 итерация. Середина отрезка x = (0 + 0,5) / 2 = 0,25

Значение функции в середине

¦(x)=¦(0,25)= 0,253+2·0,25-1=0,0115625-0,5=-0,484375

Функция не меняет свой знак на первой половине отрезка, поэтому отбросим ее: x* Î [0,25;0,5]

Вычисления следует продолжить до достижения требуемой точности. Например, если ε=0,001 то потребуется не менее 10 итераций:

 

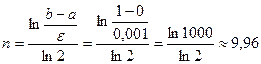
3.2.2. Метод простых итераций (метод последовательных приближений).

Метод реализует стратегию постепенного уточнения значения корня.

Постановка задачи. Дано нелинейное уравнение (3.1). Корень отделен x^* Î [a;b]. Требуется уточнить корень с точностью ε.

Уравнение (3.1) преобразуем к эквивалентному виду x=φ(x), (3.7)

что можно сделать всегда и притом множеством способов.

Выберем начальное приближение x₀Î [a;b].

Вычислим новые приближения:

x₁=φ(x₀)

x₂=φ(x₁)

………..

x_i=φ(x_i-1), i=1,2,… где i − номер итерации. (3.8)

Последовательное вычисление значений x_i по формуле (3.8) называется итерационным процессом метода простых итераций, а сама формула - формулой итерационного процесса метода.

Если 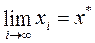, то итерационный процесс сходящийся.

Условие сходимости 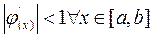(3.9)

Точное решение x^* получить невозможно, так как требуется бесконечный итерационный процесс.

Можно получить приближенное решение, прервав итерационный (3.8) при достижении условия

, (3.10)

где ε - заданная точность; i - номер последней итерации.

В большинстве случаев условие завершения итерационного процесса (3.10) обеспечивает близость значения x_i к точному решению:

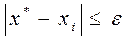
Рассмотрим геометрическую иллюстрацию метода простых итераций.

Уравнение (3.7) представим на графике в виде двух функций: y₁ = x и y₂= φ(x).

Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.

 

 

 

 

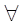Рис. 3.7 Итерационный процесс для случая 0< <1 xÎ[a,b].

 

 

Рис. 3.8 Итерационный процесс для случая -1< <1 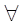xÎ[a,b].

 

Рис. 3.9 Итерационный процесс для случая >1 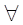xÎ[a,b].

 

Рис. 3.10 Итерационный процесс для случая £ - 1 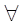xÎ[a,b].

Из анализа графиков следует, что скорость сходимости растет при уменьшении значения

Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).

При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.

 

 

 

Рис 3.11. Алгоритм решения нелинейного уравнения методом
простых итераций:

 

Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование (3.1) в (3.7), чтобы обеспечивалось условие сходимости (3.9).

Простейшие эквивалентные преобразования, например:

f(x) = 0 => x+f(x) = x, т.е. φ(x) = x + f(x)

или выразить явно x из (3.1)

f(x) = 0 => x - φ(x) = 0 => x = φ(x)

не гарантируют сходимость.

Рекомендуется следующий способ получения формулы сходящегося итерационного процесса.

Пусть .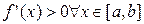

Если это не так, переписать уравнение (3.1) в виде

Умножить обе части уравнения на 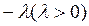и к обеим частям прибавить x:

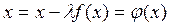
Константу l вычислить по формуле:

(3.11)

Такое значение λ гарантирует сходящийся итерационный процесс по формуле

x_i = x_i+1− λ f(x) (3.12)

где i=1,2,… - номер итерации, x₀Î[a,b] – начальное приближение.

Пример 3.2.

Методом простых итераций уточнить корень уравнения x³=1-2 x с точностью ε=0,001. Корень отделен ранее (см. пример 3.1), x^* Î [0;1].

Сначала нужно получить формулу сходящегося итерационного процесса.

Из уравнения выразим явно x:

Провер