Министерство науки и высшего образования Российской Федерации
Вологодский государственный университет
Кафедра математики
ВЫСШАЯ МАТЕМАТИКА
Учебно-методическое пособие
По выполнению контрольных работ № 4, 5, 6
Институт машиностроения, энергетики и транспорта
Вологда
Задачи для контрольных заданий
Контрольная работа № 4
Тема 1. Производная.
Тема 2. Исследование функций.
Задача 1. Вычислить производные следующих функций
1.1 а)  ; б)
; б) 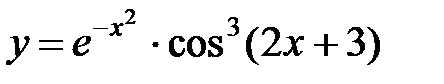 ; в)
; в)  ;
;
г) 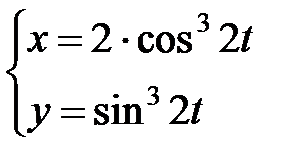 .
.
1.2 а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
1.3 а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
1.4 а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
1.5 а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
1.6 а)  ; б)
; б) 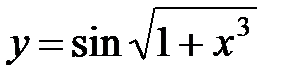 ; в)
; в)  ;
;
г)  .
.
1.7 а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
1.8 а)  ; б)
; б)  ; г)
; г)  ;
;
г)  .
.
1.9 а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
1.10 а)  ; б)
; б)  ; в)
; в)  ;
;
г)  .
.
Задача 2. Точка движется прямолинейно по закону  . Найти скорость и ускорение в момент
. Найти скорость и ускорение в момент  . Определить в какой момент скорость движения точки будет равна нулю.
. Определить в какой момент скорость движения точки будет равна нулю.
2.1  .
.
2.2  .
.
2.3  .
.
2.4  .
.
2.5  .
.
2.6  .
.
2.7  .
.
2.8  .
.
2.9  .
.
2.10  .
.
Задача 3. Провести полное исследование функции и построить ее график.
3.1  .
.
3.2  .
.
3.2  .
.
3.4  .
.
3.5  .
.
3.6 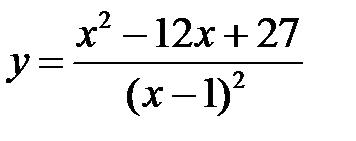 .
.
3.7  .
.
3.8  .
.
3.9 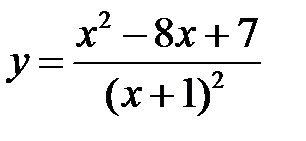 .
.
3.10  .
.
Задача 4. Приближенно решишь уравнения. Отделить корни уравнения аналитически и уточнить методом Ньютона (методом касательных)
4.1 
4.2  .
.
4.3  .
.
4.4 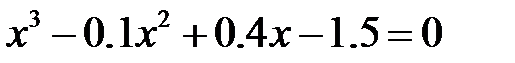 .
.
4.5  .
.
4.6  .
.
4.7  .
.
4.8  .
.
4.9  .
.
4.10 
Контрольная работа № 5
Тема 3. Неопределённый интеграл.
Тема 4. Определенный интеграл.
Задача 1. Вычислить неопределенный интеграл.
1.1 а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
1.2 а) 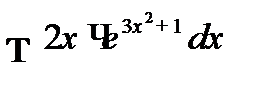 ; б)
; б) 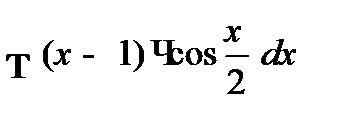 ;
;
в)  ; г)
; г)  .
.
1.3 а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
1.4 а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
1.5 а)  ; б)
; б)  ;
;
в) 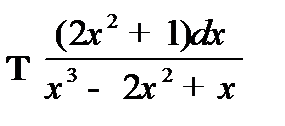 ; г)
; г)  .
.
1.6 а)  ; б)
; б) 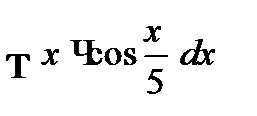 ;
;
в)  ; г)
; г)  .
.
1.7 а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
1.8 а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
1.9 а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
1.10 а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Задача 2. Вычислить определенный интеграл.
2.1 а)  ; б)
; б)  .
.
2.2 а) 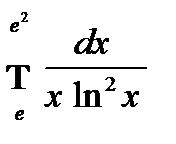 ; г)
; г)  .
.
2.3 а)  ; б)
; б)  .
.
2.4 а)  ; б)
; б)  .
.
2.5 а)  ; б)
; б)  .
.
2.6 а) 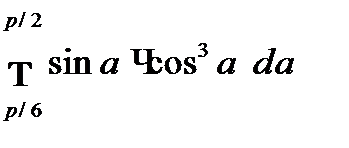 ; б)
; б)  .
.
2.7 а)  ; б)
; б)  .
.
2.8 а)  ; б)
; б)  .
.
2.9 а)  ; б)
; б)  .
.
2.10 а)  ; б)
; б)  .
.
Задача 3. Найти площадь фигуры, ограниченной линиями.
3.1  .
.
3.2  .
.
3.3  .
.
3.4  и
и  .
.
3.5  и
и  .
.
3.6  .
.
3.7  .
.
3.8  .
.
3.9  и
и  .
.
3.10  и
и  .
.
Задача 4. Вычислить несобственный интеграл или доказать его расходимость.
4.1 а) 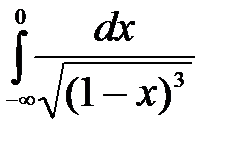 ; б)
; б)  .
.
4.2 а)  ; б)
; б)  .
.
4.3 а)  ; б)
; б) 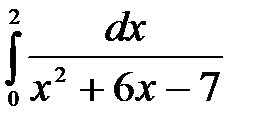 .
.
4.4 а)  ; б)
; б)  .
.
4.5 а)  ; б)
; б) 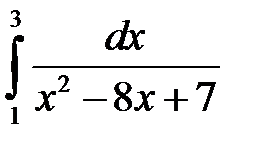 .
.
4.6 а)  ; б)
; б)  .
.
4.7 а)  ; б)
; б)  .
.
4.8 а)  ; б)
; б)  .
.
4.9 а)  ; б)
; б)  .
.
4.10 а)  ; б)
; б) 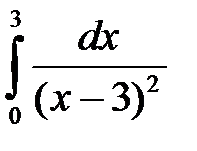 .
.
Контрольная работа № 6.
Тема 5. Функции нескольких переменных.
Задача 1. Вычислить частные производные и полный дифференциал функции  . Написать уравнение касательной плоскости и нормали к поверхности
. Написать уравнение касательной плоскости и нормали к поверхности  в точке
в точке  .
.
1.1  ,
,  .
.
1.2  ,
,  .
.
1.3  ,
,  .
.
1.4  ,
,  .
.
1.5  ,
,  .
.
1.6  ,
, 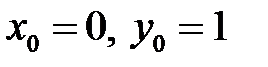 .
.
1.7  ,
, 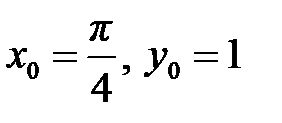 .
.
1.8 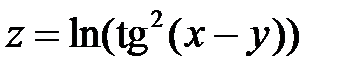 ,
, 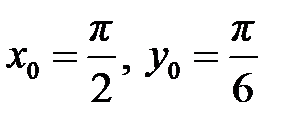 .
.
1.9  ,
,  .
.
1.10  ,
,  .
.
Задача 2. Найти линейную зависимость между величинами  где
где  . Параметры
. Параметры  вычислить методом наименьших квадратов.
вычислить методом наименьших квадратов.
2.1
| X | ||||||||||

| 4,2 | 2,8 | 5,7 | 10,5 | 13,2 | 20,5 | 33,4 | 46,9 | 60,1 | 71,2 |
2.2
| X | ||||||||||

|
2.3
| X | ||||||||||

| 4,2 | 3,2 | 2,9 | 2,5 | 2,45 | 2,15 | 2,00 | 1,75 | 1,9 | 1,6 |
2.4
| X | ||||||||||

| 4,4 | 5,1 | 5,4 | 6,7 | 6,2 | 7,5 | 7,7 | 9,2 | 9,9 | 11,5 |
2.5
| X | ||||||||||

| 4,9 | 6,5 | 7,1 | 7,9 | 8,1 | 8,9 | 8,6 | 9,1 | 9,5 | 9,7 |
2.6
| X | ||||||||||

|
2.7
| X | ||||||||||

|
2.8
| X | ||||||||||
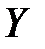
| - 2 | - 12 | - 15 | - 19 | - 35 | - 35 | - 47 | - 55 | - 60 | - 69 |
2.9
| X | ||||||||||

|
2.10
| X | ||||||||||

| 6,8 | 5,8 | 5,0 | 4,3 | 3,6 | 3,6 | 3,1 | 2,9 | 2,5 | 2,3 |
Разбор задач контрольной работы № 4
Тема 1. Производная.
Тема 2: Исследование функйий.
Задача 1. Вычислить производные следующих функций
а) 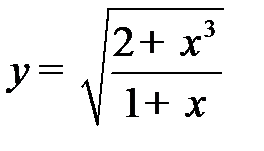 ; б)
; б)  ;
;
в)  ; г)
; г) 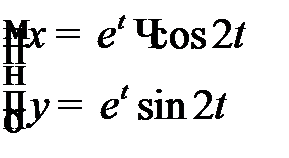 .
.
Решение.
а) Вычислим производную функции 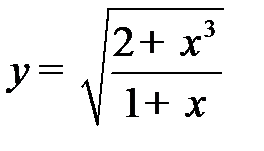 .
. 

 .
.
б) Вычислим производную функции  .
.


 .
.
в) Вычислим производную функции 

 .
.
г) Вычислим производную функции заданной параметрически
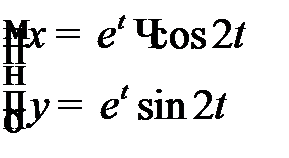
 , где
, где
 и
и
 .
.
Тогда  .
.
Задача 2. Точка движется прямолинейно по закону  м. Найти скорость и ускорение в момент
м. Найти скорость и ускорение в момент  сек. Определить в какой момент скорость движения точки будет равна нулю.
сек. Определить в какой момент скорость движения точки будет равна нулю.
Решение.
Скорость движения точки  . В момент
. В момент  сек.
сек.  .
.
Ускорение  . В момент
. В момент  сек.
сек.  .
.
Скорость движения точки равна если  . Корень уравнения
. Корень уравнения  не имеет смысла. Таким образом скорость движения точки равна нулю в начальный момент и через 5 сек. после начала движения.
не имеет смысла. Таким образом скорость движения точки равна нулю в начальный момент и через 5 сек. после начала движения.
Задача 3. Провести полное исследование функции и построить ее график.
 .
.
Решение.
1) Область определения функции:  .
.
2) Область значений функции:  .
.
3) Свойствами чётности или нечетности функция не обладает т.к.  .
.
4) График функции проходит через начало координат  ;
;
 при
при  и
и  при
при  .
.
5) Исследуем функцию на экстремумы и монотонность.

Критическими точками являются точки  .
.
 т.е. функция возрастает при
т.е. функция возрастает при 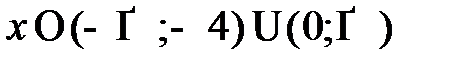 ;
;
 т.е. функция убывает при
т.е. функция убывает при  .
.
Таким образом функция имеет максимум  при
при  и минимум
и минимум  при
при  .
.
6) Исследуем функцию на выпуклость и вогнутость и точки перегиба.

 .
.
Критическими точками являются точки  .
.
 т.е. график функции является выпуклым при
т.е. график функции является выпуклым при  и
и  т.е. график функции является вогнутым при
т.е. график функции является вогнутым при  . Точки перегиба отсутствуют.
. Точки перегиба отсутствуют.
7) Определим асимптоты графика функции.
а) Точкой разрыва функции является точка  .
.
Рассмотрим поведение функции в окрестности точки разрыва.
Так как  и
и  , то прямая
, то прямая  является вертикальной асимптотой графика функции.
является вертикальной асимптотой графика функции.
б) Уравнение наклонной асимптоты имеет вид 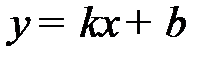 , где
, где  и
и  .
.
Таким образом наклонной асимптотой является прямая  .
.
Построим график данной функции.

Задача 4. Приближенно решишь уравнения. Отделить корни уравнения аналитически и уточнить с точностью 0,001 методом Ньютона (методом касательных)  .
.
Решение.
Вычислим производную функции  ;
;  .
.  т.к. дискриминант квадратного трехчлена
т.к. дискриминант квадратного трехчлена  , а значит функция
, а значит функция  монотонно возрастает при всех
монотонно возрастает при всех  . Таким образом данное уравнение имеет единственный действительный корень. Отделим этот корень аналитически, для этого составим таблицу
. Таким образом данное уравнение имеет единственный действительный корень. Отделим этот корень аналитически, для этого составим таблицу

| ||

| – | + |
Итак уравнение имеет единственный действительный корень  . Уточним корень методом Ньютона (методом касательных).
. Уточним корень методом Ньютона (методом касательных).
Вычислим вторую производную данной функции  при
при  , то за начальное приближение примем
, то за начальное приближение примем  , т.к.
, т.к.  . Вычисления производим по формуле
. Вычисления производим по формуле  . вычисления проводятся до тех пор, пока
. вычисления проводятся до тех пор, пока 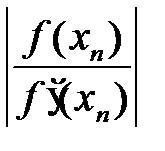 не станет меньше 0,001. Составим таблицу
не станет меньше 0,001. Составим таблицу

| 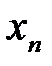
| 
| 
| 
| 
|
| 0,4 | 4,4 | 0,090909 | 0,909091 | ||
| 0,909091 | 0,060406 | 4,054545 | 0,014898 | 0,894193 | |
| 0,894193 | 0,009172 | 3,997932 | 0,002294 | 0,891899 | |
| 0,891899 | 0,001389 | 3,989214 | 0,000348 | 0,89155 | |
| 0,89155 | 0,00021 | 3,987892 | 5,27E-05 | 0,891498 |
Ответ:  .
.
Разбор задач контрольной работы № 5
Тема 3. Неопределённый интеграл.
Тема 4. Определенный интеграл.
Задача 1. Вычислить неопределенный интеграл.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Решение.
а)  . Для вычисления данного интеграла выполним замену переменных
. Для вычисления данного интеграла выполним замену переменных  и
и  . Тогда
. Тогда  .
.
б)  . Для вычисления данного интеграла используем формулу интегрирования по частям
. Для вычисления данного интеграла используем формулу интегрирования по частям  . Пусть функция
. Пусть функция  и дифференциал
и дифференциал  . Найдем
. Найдем  . Тогда
. Тогда  .
.
в)  . Разложим подынтегральную рациональную дробь в сумму простейших дробей с неизвестными коэффициентами
. Разложим подынтегральную рациональную дробь в сумму простейших дробей с неизвестными коэффициентами  . Для того, чтобы найти неизвестные коэффициенты выполним преобразования:
. Для того, чтобы найти неизвестные коэффициенты выполним преобразования: 
Сравнивая полученную дробь с исходной, составим и решим систему уравнений  . Тогда
. Тогда 

 ,
,
г)  . Для вычисления этого интеграла используем универсальную тригонометрическую подстановку
. Для вычисления этого интеграла используем универсальную тригонометрическую подстановку  . При этом
. При этом  . Тогда
. Тогда 
 .
.
Задача 2. Вычислить определенный интеграл.
2.1 а)  ; б)
; б) 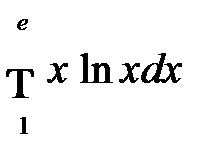 .
.
Решение.
а)  . Пусть
. Пусть  , тогда
, тогда  , и
, и  . Вычислим интеграл
. Вычислим интеграл 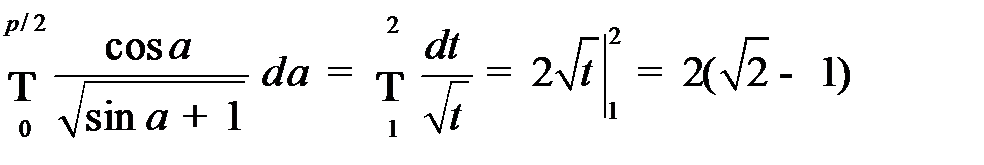 .
.
б) 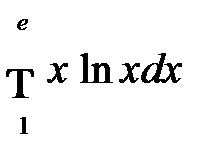 . Интегрируя по частям, обозначим
. Интегрируя по частям, обозначим  . Тогда
. Тогда  .
.
Задача 3. Найти площадь фигуры, ограниченной линиями.
 при
при  .
.
Решение. Найдем точки пересечения линий. Для этого решим уравнение 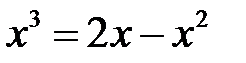 . Корни этого уравнения
. Корни этого уравнения 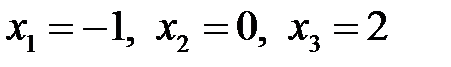 .
.

Вычислим площадь фигуры, расположенной в первой четверти  .
.
Задача 4. Вычислить несобственный интеграл или доказать его расходимость.
Решение.
а)  . По определению несобственный интеграл первого рода
. По определению несобственный интеграл первого рода 
 .
.
б)  . Так как подынтегральная функция имеет бесконечный разрыв в точке
. Так как подынтегральная функция имеет бесконечный разрыв в точке  , то вычислим несобственный интеграл второго рада
, то вычислим несобственный интеграл второго рада 
 . Интеграл расходится.
. Интеграл расходится.