ПОКАЗАТЕЛЬ КАЧЕСТВА – количественная характеристика свойств продукции, входящих в состав её качества, рассматриваемая применительно к определенным условиям её создания и эксплуатации.
КЛАССИФИКАЦИЯ ПОКАЗАТЕЛЕЙ:
1) по количеству характерных свойств:
§ частные (единичные)
§ комплексные
§ определяющие
§ интегральные
Показатель качества, относящийся только к одному свойству называется единичным, а относящийся сразу к нескольким свойствам – комплексным.
Показатель качества продукции, относящийся к такому её свойству или к такой совокупности свойств, по которым принимают решение оценивать качество, называют определяющими (обобщенными) показателями.
Комплексный показатель качества продукции, отражающий соотношение суммарного полезного эффекта от эксплуатации или потребления продукции к суммарным затратам на её создание и эксплуатацию называется интегральным.
где ∏ ∑ - положительный эффект;
Зс+Зэ – сумма затрат.
2) по способу выражения свойств:
§ натуральные;
§ денежные;
§ балльные.
3) по применению для оценки:
§ базовые (показатели базового образца или эталона);
§ показатели оцениваемой продукции;
§ относительные.
4) по видам свойств объектов
§ показатели назначения;
§ показатели надёжности;
§ показатели экономного использования ресурсов;
§ эргономические;
§ эстетические;
§ показатели технологичности;
§ показатели транспортабельности;
§ показатели стандартизации и унификации;
§ патентно-правовые показатели;
§ экологические;
§ безопасности;
§ экономические.
Показатели назначения
Характеризуют свойства, определяющие основные функции, для которых предназначено изделие.
|
|
ПОКАЗАТЕЛИ НАЗНАЧЕНИЯ
1. Классификационные показатели назначения характеризуют принадлежности продукции к определенной классификационной группе. Например, мощность двигателя, быстрота действия процессора, погрешность измерительного прибора, содержание углерода в стали.
2. Функциональные показатели (показатели эффективности использования) характеризуют полезный эффект от эксплуатации или потребления продукции и прогрессивность закладываемых в продукцию технических решений. Например, грузоподъёмность транспортного средства, калорийность пищевых продуктов.
3. Конструктивные показатели характеризуют основные проектно-конструкторские решения, удобство монтажа, установки продукции, возможность её взаимозаменяемости. Например, габаритные размеры, коэффициент сборности.
где Qc – количество специфицируемых составных частей изделия;
Qн - количество неспецифицируемых составных частей изделия;
Qоб – общее количество составных частей.
4. Показатели структуры и состава характеризуют содержание в продукции химических элементов или структурных групп. Например, концентрация примеси в растворе, структурный состав фасованных пищевых продуктов.
Показатели назначения фиксируются в технических заданиях на разработку продукции, технических условиях, паспорте изделия, и другой сопроводительной документации.
Состав показателей назначения специфичен для данного изделия.
Пример: типовой состав показателей назначения бытового радиоприёмника:
- границы и состав частотных диапазонов;
|
|
- чувствительность;
- помехозащищенность по диапазону;
- вид звукового выхода (моно/стерео);
- характер использования (стационарный, переносной);
- вид настройки (ручной или автоматический);
- материал корпуса;
- габариты;
- масса.
Показатели назначения включаются в стандарты производителей продукции (СТО), в инструкции по эксплуатации и другую сопроводительную документацию и являются объектом рекламы.
Показатели надёжности
Надёжность – свойство объекта выполнять установленные функции, сохраняя свои показатели в заданных пределах в течении требуемого промежутка времени.
Надежность – свойство сложное, состоит из 4-х более простых свойств:
· безотказность;
· долговечность;
· ремонтопригодность;
· сохраняемость.
Схема основных состояний изделия и событий, приводящих к ним.
Расшифровка событий при изменении состояний:
1- повреждение;
2- отказ;
3- переход в предельное состояние;
4- восстановление;
5- ремонт.
Исправное состояние – состояние объекта, при котором он соответствует всем требованиям нормативно-технической документации.
Переход из исправного в поврежденное состояние происходит в результате повреждения.
Повреждение – событие, заключающееся в нарушении исправного состояния при сохранении работоспособного состояния.
Неработоспособное состояние – состояние, когда значения хотя бы одного параметра изделия не соответствуют требованиям нормативно-технической документации. В это состояние изделие переходит в результате отказа.
Предельное состояние – состояние объекта, при котором его дальнейшее применение по назначению недопустимо или целесообразно.
|
|
Существует изделия восстанавливаемые и невосстанавливаемые, ремонтируемые и неремонтируемые.
ПОКАЗАТЕЛИ БЕЗОТКАЗНОСТИ
ГОСТ 27.003 – 83 «Выбор и нормирование показателей надёжности».
Безотказность – свойства объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или некоторой наработки.
Наработка - продуктивность работы объекта в единицах времени.
1) Вероятность безотказной работы – вероятность того, что в пределах заданной наработки t отказ объекта не возникнет.
Р(t)= Р(Т≥t),
где Р – вероятность безотказной работы;
Т – время от начала работы до отказа.
0≤Р(t) ≤1
Р(0)=1, Р(∞)→0
Статистическая оценка вероятности безотказности работы
P(t)=N(t)/N0
Где N0 – число объектов в начале испытаний,
N(t) – число объектов, исправно работающих в интервале [0;t].
2) Вероятность отказа Q(t)=1-P(t)
Где N0 – число объектов в начале испытаний,
N(t)́ – число отказавших изделий за время t.
3) Средняя наработка на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течении этой наработки.
tсрi - время исправной работы между (i-1)ым и i-ым отказами
n – число отказов объекта.
4) Интенсивность отказа – отношение числа отказавших объектов в единицу времени к среднему числу объектов, продолжающих исправно работать в данный интервал времени.
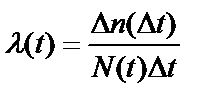где ∆t – интервал времени;
∆n (∆t) – число отказов в интервале [t-∆t/2; t+∆t/2];
где Ni-1 – число исправно работающих объектов в начале интервала ∆t;
Ni - число исправно работающих объектов в конце интервала ∆t;
N(t) – среднее число объектов, продолжающих исправно работать в данном интервале времени.
При внезапном отказе параметры объекта меняются скачкообразно, при постепенном – медленно.
Интенсивность отказов показывает, какая часть объектов выходит из строя в единицу времени по отношению к среднему числу исправно работающих объектов.
Р(t)=exp (∫λ(t)dt, если λ=const, то Р(t)= =exp (-λ(t)) – основное уравнение теории надёжности
5) Параметр потока отказа – отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки.
При этом время восстановления не учитывается, считается, что изделие восстанавливается мгновенно.
– параметр потока отказа,
6) Частота отказа – отношение числа отказавших изделий в единицу времени к первоначальному числу испытываемых изделий при условии, что все вышедшие из строя изделия не восстанавливаются. 
где ∆n (∆t) – число отказов в интервале [t-∆t/2; t+∆t/2];
N0 – общее число изделий в начале испытания.
ОБЕСПЕЧЕНИЕ БЕЗОТКАЗНОСТИ
Для обеспечения безотказности используют метод резервирования.
РЕЗЕРВИРОВАНИЕ – способ повышения безотказности путём параллельного включения в систему резервных дополнительных элементов, способных в случае отказа основного элемента выполнить его функции.
Любую техническую систему можно представить в виде совокупности последовательно соединенных элементов.
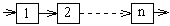
Вероятность безотказной работы системы из n элементов:
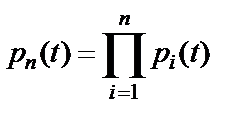
Отказ любого элемента приводит к отказу всей системы.
Существует три метода резервирования:
· общее
· раздельное
· комбинированное
Общее резервирование - такое резервирование, при котором параллельно основной подключаются другие идентичные системы. Эти системы называются резервными.
Схема общего резервирования.
Раздельное резервирование – резервирование отдельных элементов системы изделий в n звеньев.
Схема раздельно резервирования.
При комбинированном резервировании применяется как общее так и раздельное резервирование.
РАСЧЁТ НАДЁЖНОСТИ
Общее резервирование
Вероятность отказа j-ой параллельной цепи: 
Вероятность отказа всей системы из (m+1) цепи: 
Пусть все цепи одинаковы: 
Вероятность безотказной работы: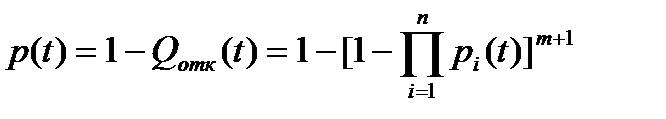 
Все элементы равнонадёжные: 