Тема: Показательные неравенства.
Дата: 19.10.2021 г.
Группа: ПЦ-265
Цель урока:
введение понятия «показательные неравенства» и методов их решения
Изучив тему, учащиеся должны:
Знать:
- определение показательного неравенства;
- методы решения показательных неравенств;
- классификацию типов показательных неравенств по методу решения.
Уметь:
- решать показательные неравенства различными способами;
- применять полученные знания для решения практических задач;
- анализировать полученную информацию;
- уметь проводить взаимоконтроль и самоконтроль учебной деятельности
Актуализация знаний студентов
Сегодня на уроке, мы рассмотрим показательные неравенства и основные методы их решения, что даст нам возможность решать их уверенно и быстро. Для начала предлагаю вспомнить методы решения показательных уравнений, так как они аналогичны методам решения показательных неравенств.
- Сведение к одному основанию.
- Вынесение общего множителя за скобки.
- Метод введения новой переменной.
- Графический.
А теперь вспомните свойства показательной функции
1) Область определения – R (множество всех действительных чисел).
2) Множество значений – множество всех положительных чисел.
3) Показательная функция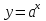 
является возрастающей на множестве всех действительных чисел, если 
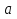>1, и убывающей, если 0< 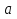<1.
Изучение нового материала.
Итак, при решении показательных неравенств необходимо использовать 3-е свойство показательной функции:
1. Если 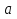>1, то неравенство ах>ab,справедливо тогда и только тогда, когда a>b.
2. Если 0< 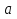<1, то неравенство ах>ab, справедливо тогда и только тогда, когда a<b.
Запишите в тетрадях
|
|
Показательные неравенства.
1. Если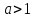 
, то неравенство ах>ab Û х>b.
2. Если 0< 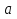<1, то неравенство ах>ab Û х<b.
Давайте запишем определение показательного неравенства.
Показательное неравенство – это неравенство вида ах>ab, где а>0, а≠1.
А теперь приступаем к разбору ключевых примеров.
Пример 1. Решить неравенство: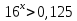 
(метод приведения к одному основанию). Перепишем неравенство: 
; 
; 
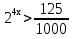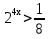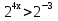.Т. К 2>1, то по свойству 1 знак остаётся прежним, т. е. 
⇒ 
.
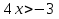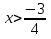Ребята, важно отметить, что ответ можно записать либо в виде неравенства, либо в виде промежутка. Запишем в виде промежутка.
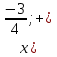
Ответ: ()
Пример 2. Решить неравенство: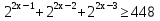 
.
Как вы думаете, какой метод используется здесь?
Метод вынесения общего множителя за скобки:
.
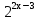Потому что за скобки выносится наименьшая степень.
Продолжим: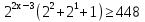 
; 
; 
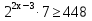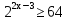(т. к 2>1, то по свойству 1 знак остаётся прежним) ⇒ 
⇒ 
⇒ 
.
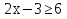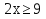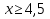Ответ: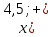 
Запись тетрадях:
; ; ; ⇒ ⇒ ⇒ .
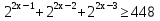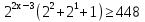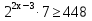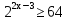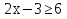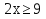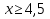Ответ: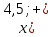
Пример 3. Решить неравенство: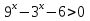 
.
Здесь, как вы видите, лучше использовать метод введения новой переменной. Пусть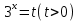 
⇒ 
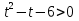. У нас получилось квадратное неравенство, которое решается методом интервалов.
Для начала найдём корни, т.е. от неравенства перейдём к уравнению: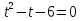 
⇒ 
.
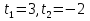Отмечаем их на числовой прямой, у нас получилось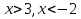 
⇒ 1)Неравенство 
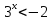–решений не имеет, т.к. корень 
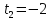не удовлетворяет нашему условию 
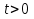; 2)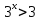 
, т.к. 3>1⇒ 
.
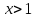Ответ: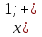 
Запись в тетрадях:
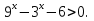Пусть ⇒ , ⇒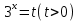
⇒ 
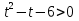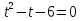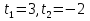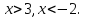
1) 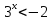–решений не имеет, т.к. корень 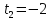не удовлетворяет нашему условию ,
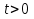2) 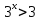, т.к. 3>1⇒ .
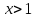Ответ: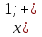
Закрепление изученного материала.
Ну, а теперь, закрепим полученные знания.
|
|
Сегодня мы должны решить номера №228(1,3,5)-устно,
№229(1), №231(1,2) и №232(1,3).
№228(1) устно
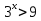. Т.к. 3>1, то 
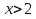. Ответ: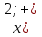 
№228(3) устно
; 
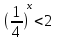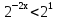. Т.к. 2>1, то 
⇒ 
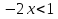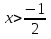. Ответ: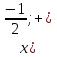 
№229(1)
, 
⇒ 
⇒ 
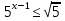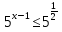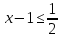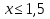. Ответ: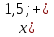 
Запись в тетрадях:
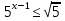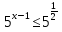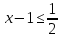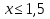, ⇒ ⇒ . Ответ: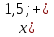
№231(1)
, 
, 
, 
, 
⇒ 
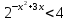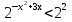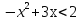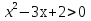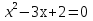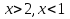. Ответ: .
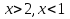Запись в тетрадях:
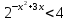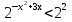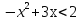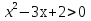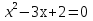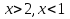, , , , ⇒ . Ответ: .
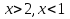№231(2)
, 
, 
⇒ 
, 
⇒ 
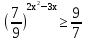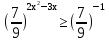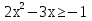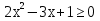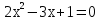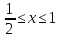. Ответ: .
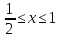Запись в тетрадях:
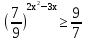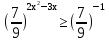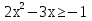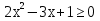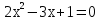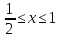, , ⇒ , ⇒ . Ответ: .
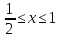№232(1)
, 
, 
· 
, 
⇒ 
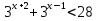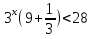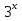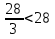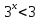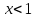. Ответ: .
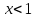Запись в тетрадях:
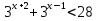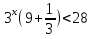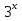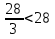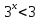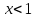, , · , ⇒ . Ответ: .
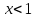№232(3)
, 
, 
· 
, 
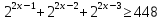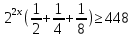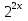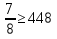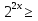512⇒
⇒ 
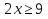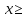4,5. Ответ: .
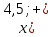Запись в тетрадях:
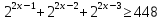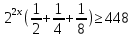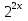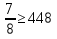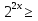, , · , 512⇒
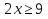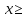⇒ 4,5. Ответ: .
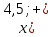Подведение итогов.
Что нового вы узнали сегодня на уроке?
Узнали, что такое показательные неравенства и научились их решать.
Так что называется показательным неравенством?
Показательное неравенство – это неравенство вида ах>ab, где а>0, а≠1.
Домашнее задание.
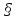13, №231(3,4), №232(2,4), №233(1).
Критерии оценивания:
1.Оценка «отлично» - выставляется обучающемуся, если правильно решены все задания, выполнены в полной мере, изложены логично.
1. Оценка «хорошо» - выставляется обучающемуся, если допущены незначительные погрешности в задании.
2. Оценка «удовлетворительно» - выставляется обучающемуся, если ответ на вопрос нелогичный, не полный.
3. Оценка «неудовлетворительно» - выставляется обучающемуся, если задания не решены.
ВНИМАНИЕ!!!
Уважаемые студенты, практическое задание необходимо выполнить в рабочей тетради (сфотографировать) или в формате Документа Word. Отправлять для проверки в личные сообщения на страницу ВКонтакте:https://vk.com/kolomiyetssg?z=photo95751036_324720501%2Falbum95751036_0%2Frev
Преподаватель: Коломиец Светлана Григорьевна
|
|