Растягивающее напряжение в шипе

s _рш=С_рш/(z_шF_ш)= rw²F_бr_бt_б/z_шF_ш,

где F_ш- площадь поперечного сечения шипа; z_ш- количество шипов на лопатке.

Результаты расчетов на прочность шипа и ленточной бандажной связи сведены в таблицу 6.1.

6.2. Расчет пера лопатки на растяжение

К расчету пера лопатки на растяжение

Рис. 6.2

Центробежную силу профильной части лопатки (рис. 6.2) с постоянным по высоте профилем определяют по формуле

С_Р=rF_лlrw²,

где r- плотность материала лопатки;

F_л- площадь поперечного сечения лопатки; l- длина лопатки; r- средний радиус облопачивания, на котором лежит центр тяжести лопатки; w-угловая скорость вращения.

Напряжение растяжения от центробежной силы, развиваемой массой лопатки в корневом сечении равно:

s_p=C_p/F_л=rlrw²

Как видно из формулы, напряжения растяжения лопатки постоянного профиля пропорциональны квадрату частоты вращения, длине, среднему радиусу и не зависят от площади сечения лопатки.

В том случае, когда лопатки скреплены в пакеты ленточными бандажами, в корневом сечении, помимо центробежной силы собственной массы лопатки, действуют центробежные силы бандажей.

Центробежная сила ленточного бандажа определяется следующим образом:

С_б=rF_бt_бr_бw²,

Тогда суммарное напряжение растяжения в корневом сечении лопатки равно:

s_p=(C_л+С_б)/F_л.

6.3. Расчет лопатки на изгиб от парового усилия

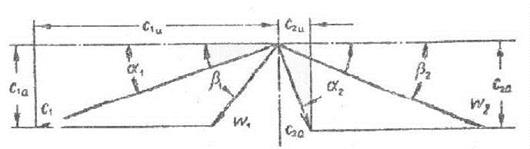
Действие пара на лопатку обуславливает возникновение силы, которая может быть разложена на окружную составляющую P_u и осевую P_a. Обе силы относятся к массе, проходящей через лопаточный канал. P_u может быть определена из уравнения количества движения:

P_u=G(c_1u-c_2u)/ez₂, где G- массовый расход пара через ступень, кг/сек; e- степень парциальности; z₂-число рабочих лопаток; с_1u- проекция абсолютной скорости выхода пара из сопел на направление окружной скорости, м/сек; с_2u- проекция абсолютной скорости выхода пара из рабочих лопаток на направление окружной скорости, м/сек.

Осевая составляющая парового усилия обуславливается как динамическим действием рабочей среды при обтекании лопатки, так и разностью статических давлений по обе стороны лопатки:

P_a=G(c_1a-c_2a)/(ez₂)+(p₁-p₂)t₂l, где с_1а и с_2а- осевые составляющие скоростей (см. рис. 6.3), м/сек; p₁ и p₂-давление перед и за рабочей решеткой, Па; t₂-шаг лопаток, м; l-высота лопатки, м.

Треугольники скоростей турбинной ступени

Рис. 6.3

При подсчете сил по приведенным выше формулам необходимо выбирать режим работы турбины, при котором окружное усилие достигает максимальной величины. Для большинства ступеней турбины, и в особенности для последней ступени, таким режимом является максимальная нагрузка турбины: для первой ступени паровой турбины с сопловым парораспределением опасным режимом служит нагрузка, соответствующая полному открытию первого регулирующего клапана (остальные клапаны закрыты), когда ступень работает с большим тепловым перепадом и малой парциальностью.

Равнодействующая сил P_u и P_a (рис. 6.4) равна их геометрической сумме:

.

Силы, изгибающие лопатку

.

Рис. 6.4

Для определения напряжений изгиба необходимо найти положение главных центральных осей инерции сечения –h и x -x, проходящих через центр тяжести профиля 0. Силы, действующие в плоскостях наименьшей (ось h–h) и наибольшей (ось x- x) жесткости профиля, обозначенные соответственно P₁ и P₂, находятся следующим образом:

,

где j-угол между направлением силы Р и перпендикуляром оси минимального момента инерции.

Данная методика довольна сложна, поэтому для расчетов применяются следующие упрощения:

1) ось x- x минимального момента инерции без большой погрешности может быть принята параллельной хорде профиля mn (рис.6.4);

2) направление силы Р может быть принято совпадающим с осью h–h, так как угол j между ними обычно невелик и cosj »1.

Таким образом, определив по формуле M_к=Рl/2 изгибающий момент от газовых сил, можно найти максимальное напряжение изгиба в обеих кромках корневого сечения:

(s_u)_кр=M_кe₁/I_min=M_к/W_кр,

и в спинке

(s_u)_сп=M_кe₃/I_min=M_к/W_сп.

В формулах через I_min обозначен момент инерции сечения профиля относительно оси x- x, а через W_кр и W_сп –минимальные моменты сопротивления соответственно кромки и спинки сечения лопатки относительно той же оси. Напряжениями в кромках, вызванными моментом от проекции силы Р на ось x- x, т.е. силой Р₂, можно пренебречь.

На лопатку, изогнутую силами пара, действует центробежная сила ее массы, которая стремится выпрямить лопатку и поэтому создает момент, обратный моменту сил пара. С учетом этого влияния центробежной силы результирующий изгибающий момент равен не величине М, а cМ, где c - так называемый коэффициент разгрузки, меньший единицы. В данной работе расчет коэффициента разгрузки отсутствует.

Расчет пера лопатки на растяжение от центробежных сил и на изгиб от паровых сил сведен в табл. 6.2.

6.4. Расчет Т- образного хвостовика

При расчете хвостовиков обычно определяют лишь центробежную силу лопатки, которая может вызвать в хвостовике растягивающие, изгибающие, сминающие и срезывающие напряжения. Напряжения изгиба, возникающие от усилий пара, не учитываем, т.к. при плотной пригонке хвостовиков соседних лопаток одного к другому эти напряжения не велики.

Для расчета на прочность задаемся в зависимости от ширины лопатки размерами хвостовика (см. рис. 6.5):

Т- образный хвостовик лопатки

Рис.6.5

T=0.4B м;

h₁=0.4B м;

Ф=0,7В м;

h₂=0.3B м.

При дальнейших расчетах эти отношения уточняются.

Наибольшие растягивающие напряжения возникают в сечении АВ хвостовика.

Сумму центробежных сил пера лопатки и бандажа, т.е. сил, развиваемых массами, лежащими над сечением MN, обозначим SС; центробежную силу части хвостовика, ограниченную линиями MN и АВ, -через С’_х.

Площадь поперечного сечения хвостовика по АВ определяется площадью фигуры befd,обозначим ееf₁. В таком случае растягивающее напряжение

.

Напряжения среза в сечениях AD и BC хвостовика

,

где С”_Х- центробежная сила участка ABCD; ¦₂- площадь среза.

По площадкам abdc и eghf в хвостовике возникает напряжение смятия

,

где С_Х- полная центробежная сила хвостовика (между сечениями MN и хх); ¦₃ площадь abdc или eghf (действительная площадь прилегания хвостовика за вычетом фасок и галтелей).

Результаты расчетов сведены в табл. 6.3.

Из расчетов на прочность видно, что элементы рабочих лопаток проходят на прочность с необходимым запасом.