1) Выбирают способ назначения балльных оценок весомости, способ выполнения контрольной операции; опрашивают экспертов и получают индивидуальные экспертные оценки.
2) Проверяют индивидуальные оценки каждого эксперта на внутреннюю непротиворечивость. В случае обнаружения противоречий проводят повторный опрос экспертов.
3) Проверяют согласованность индивидуальных оценок между собой и выявляют выпадающие индивидуальные оценки и отдельные внутренние согласованные группы оценок (еретиков и школы).
4) В случае обнаружения еретиков и школ выполняют следующие действия:
- проводят собрания экспертной группы, на котором обсуждают обнаруженные разногласия и выполняют повторное назначение оценок;
- если оценки вновь рассогласованы, то принимают решение выполнять дальнейшую разработку в нескольких вариантах в зависимости от количества обнаруженных согласованных групп оценок;
- если это решение не может быть выполнено, то расформировывают экспертную группу и выбирают другой способ ее формирования.
5) Определение обобщённых коэффициентов весомости (усреднение оценок по всем экспертам).
6) Производят нормирование коэффициентов весомости в каждой группе показателей по всем уровням дерева свойств. Исключение малозначимых показателей и перенормировка.
Нормирование: 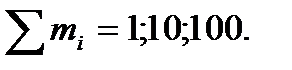
где  - сумма коэффициентов на данном уровне
- сумма коэффициентов на данном уровне
3 способа определения коэффициентов весомостей:
1. способ вспомогательной шкалы
2. способ парных сравнений
3. стоимостной способ
Экспертные кривые
Экспертные кривые – это графики, изображающие зависимость между значениями 2-х показателей, построенные на основе экспертных суждений.
Они предназначены для того, чтобы дать наглядную интерпретацию анализируемого явления, выявить характерные элементы анализируемой зависимости и найти параметры этих характерных элементов.
Кривые полезности (желательности)
Эти кривые применяют для отображения уровня удовлетворения некоторой потребности субъекта в зависимости от значения анализируемого показателя.
Пример
Пусть разрабатывается конструкция нового строительного механизма. Требуется изобразить желательность для оператора усилий при перемещении рычага управления.
4 балла – оптимальные усилия; 1 балл – неприемлемые усилия.
| усилия, Н |
| желательность |
Задача анализа сводится к поиску характерных элементов (ХЭ).
Можно выявить два характерных элемента:
- плато оптимума усилий вблизи 20 Н;
- кривизна кривой больше слева, со стороны меньших усилий, чем справа.
Изготовителю важно обеспечить, чтобы усилия укладывались в ширину плато, если это невозможно, то выгоднее смещать усилия в большую сторону, так как снижение оценки желательности здесь происходит медленнее.
Кривые безразличия
Их проводят в системе координат, образованной двумя показателями так, чтобы соединить точки, соответствующие равнопредпочтительными комбинациями значений показателей.
По одну сторону от кривой оказывается сочетание значений, каждый из которых предпочтительнее любого сочетания, находящиеся по другую сторону.
Назначение кривых безразличия: сравнение объектов, нахождение оптимальных комбинаций показателей.
Пример
Пусть разрабатывается конструкция мотора для прогулочного катера. Рассматривается два показателя: масса мотора m, максимальная скорость катера vmax.
Масса может изменяться от 80 до 160 кг, максимальная скорость катера – от 20 до 60 км/ч. Оптимальной считается скорость 30-35 км/ч. Эта величина оценивается в 4 балла. Но она справедлива для массы 80 кг (min).
Если v=30-35 км/ч и m=100, то присваивается 3,5 балла и т.д.
| m |
| vmax |
| A |
| Б |
| опт |
Можно сравнивать конструкции: А лучше Б.