Рассмотренные выше уравнения позволяют установить общие качественные свойства движения и вычислить искомые функциональные связи с помощью математических операций. Однако во многих случаях, особенно при движении вязких жидкостей, наблюдаемые физические процессы настолько сложны, что не поддаются описанию с помощью данных уравнений. В этих случаях главную роль играют экспериментальные методы исследования, результаты которых позволяют сформулировать законы, управляющие исследуемым процессом, записать их в виде математических соотношений и установить значения коэффициентов (сопротивления, Кориолиса и др.).
Для того чтобы установить общие закономерности процессов по результатам экспериментальных исследований или использовать эти результаты в тех случаях, когда сам эксперимент непосредственно не проводился, необходимо вникнуть в сущность изучаемых процессов и произвести общий качественный анализ их. Это можно осуществить с помощью теории размерностей и подобия, в которой важная роль принадлежит безразмерным параметрам.
Числовое значение размерных (именованных) величин зависит от принятых масштабов, т.е. от системы единиц. Безразмерные (относительные) величины представляют собой отношение двух однородных физических величин, поэтому числовое значение их не зависит от выбора системы единиц (например, отношение двух длин, отношение длины во второй степени к площади и т. д.).
Аксиомы теории размерностей:
числовое значение физической величины не зависит от выбора единицы, т.е, при увеличении единицы измерения в i раз числовое значение данной физической величины уменьшается в i раз;
все члены уравнения, описывающего физический процесс, должны иметь одинаковые размерности.
Теория размерностей позволяет установить математическую зависимость исследуемой физической величины от основных (независимых) величин. В гидравлике в качестве основных величин целесообразно принимать скорость υ0, характерный линейный размер l0, живое сечение ω0 и плотность жидкости ρ0, размерности которых соответственно:
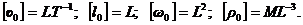
Перечисленные величины являются независимыми, так как размерность любой из них нельзя получить, комбинируя размерности двух других. В то же время, через их размерности можно выразить размерность любой величины, входящей в функциональную зависимость.
Например, известно, что сила давления потока жидкости
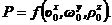
В соответствии с аксиомой теории размерностей, все члены левой и правой частей уравнения должны иметь одинаковую размерность, т. е.
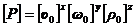(4.37)
или
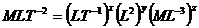. (4.38)
Определим значения показателей степени х,у, z. Так как в левой части уравнения показатель степени для М равен 1, то и в правой части z = 1. Аналогично, при значении показателя для Т, равном - 2, х = 2. Так как в левой части показатель степени для L равен 1, необходимо, чтобы и в правой части после умножения показатель при L был равен 1. Для этого определим показатель степени у из уравнения, составленного для показателей L, т. е. 1 = х + 2 у - 3 z. Подставляя в него значения х = 2, z = 1, получим у = 1. Следовательно, уравнение (4.38) примет вид: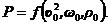 
.
В теории размерностей существует понятие безразмерного комплекса
,
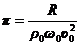позволяющего подставлять размерность в любой системе единиц.
Если имеется сложная функциональная зависимость, то для определения влияния каждой величины друг на друга пользуются π -теоремой:всякое соотношение между n -размерными параметрами, для измерения которых использовано k основных единиц υ, ω, ρ, можно представить в виде соотношения между (n - k) безразмерными комбинациями этих величин – π1, π2, π3.
Например, сила сопротивления при движении вязкой жидкости
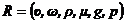
где υ - скорость жидкости; ω - живое сечение; ρ - плотность жидкости; μ - динамическая вязкость жидкости; g – ускорение свободного падения; р — давление жидкости.
Пользуясь π-теоремой, запишем:
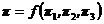(4.39)
где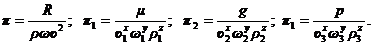 
Подставим размерности [ υ ] =LT-1, [ ω ] =L2, [ l ] = L, [ ρ ] = ML-3; [ μ ] = ML-1T-1, [ g ]=LT-2, [ p ]=ML-1Т-2; [ γ ]=[ μ/ρ ] = L2T-1 в уравнения (4.37) и (4.38). В результате решения этих уравнений получим:
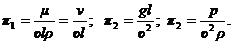
Следовательно, зависимости (4.39) можно представить в виде
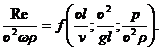(4.40)
Два явления подобны, если по известным характеристикам одного можно получить характеристики другого простым пересчетом, который аналогичен переходу от одной системы единиц к другой. Два процесса подобны, если они качественно одинаковы, а определяющие их критерии попарно равны.
Основными видами подобия являются: геометрическое, кинематическое и динамическое.
Геометрическое подобие - равенство основных относительных линейных размеров и углов: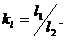 
Кинематическое подобие - подобие полей скоростей и ускорений: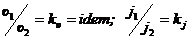 
.
Динамическое подобие существует, если выполнены условия геометрического и кинематического подобий и если соотношения сходственных сил, действующих в потоке, одинаковые, выражаемые критериями подобия.
Критерии подобия - это безразмерные степенные комплексы, которые входят в математическое описание рассматриваемого явления, составленного с помощью π-теоремы. Из зависимости (4.40) видно, что при движении потока жидкости критериями подобия будут
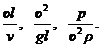
Первый критерий называется числом Рейнольдса
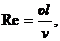
υ - скорость потока; l - характерный геометрический размер; ν - кинематическая вязкость жидкости.
Число Рейнольдса можно представить иначе:
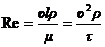(4.41)
где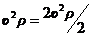 
- удвоенное динамическое давление, определяемое силой инерции; 
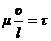- касательное напряжение в жидкости, обусловленное силой внутреннего трения (1.10).
Из выражения (4.41) ясен физический смысл числа Re - это отношение сил инерции к силам внутреннего трения. Следовательно, число Рейнольдса является определяющим критерием подобия при исследовании напорных потоков.
Второй критерий называется числом Фруда
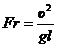(4.42)
Если правую часть выражения (4.42) умножить и разделить на плотность, то получим
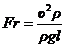(4.43)
т.е, число Фруда - это отношение динамического давления, определяемого поверхностной силой инерции, к массовой силе тяжести, отнесенной к единице площади. Число Фруда является основным критерием при исследовании безнапорных потоков.
В тех случаях, когда основными являются силы давления, критерием подобия служит третий безразмерный комплекс, называемый числом Эйлера,
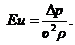(4.44)
Число Эйлера Eu - это отношение приращения силы статического давления к силе инерции, обусловленной динамическим давлением (скоростью, плотностью). Этот критерий является определяющим при исследовании движения тела в жидкости или при обтекании тела потоком.
При неустановившемся движении критерием подобия служит число Струхаля
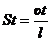, (4.45)
где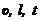 
- характерные скорость, размер и интеравл времени.
Безразмерным комплексом, характеризующим физические основы движения с учетом сжимаемости, служит число Маха (М) (1.7).
Критерии подобия Re, Fr, Eu являются основными в гидравлике при исследовании движения жидкости.