Прямые и плоскости в пространстве
Общие замечания.
Геометрическая фигура называется пространственной, если не все её точки лежат в одной плоскости.
Примером пространственной фигуры может служить геометрическое тело – часть пространства, занимаемое предметом. Геометрическое тело отделяется от окружающего пространства поверхностью.
Две геометрические фигуры называются равными, если их можно совместить так, чтобы они совпали всеми своими частями.
Предполагается, что при перемещении в пространстве геометрические фигуры не изменяются. Пространственные фигуры изображаются на чертеже в виде рисунков, которые выполняются по определённым правилам, основанным на геометрических свойствах фигур.
Основные свойства плоскости.
Основными понятиями стереометрии являются: точка, прямая и плоскость.
– через любые три точки пространства, которые не лежат на одной прямой, можно провести плоскость, и к тому же только одну;
– если две плоскости имеют общую точку, то они пересекаются по прямой, которая проходит через эту точку;
– если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Следствия:
– через прямую и точку, лежащую вне этой прямой, можно провести плоскость, и к тому же только одну;
– через две прямые, которые пересекаются, можно провести плоскость, и к тому же только одну;
– через две параллельных прямых можно провести плоскость, и к тому же только одну;
– через любую прямую в пространстве можно провести огромное количество плоскостей.
Множество плоскостей, которые проходят через некоторую прямую, называют пучком плоскостей, а прямую, через которую они проходят, – осью пучка. Плоскость на рисунку изображается в виде параллелограмма и обозначается одной буквой, например Р.

Взаимное расположение двух прямых в пространстве.
Две прямые в пространстве могут иметь такое расположение:
– две прямые лежат в одной плоскости, при этом они могут или иметь общую точку, то есть пересекаются, или не иметь общих точек, тогда их называют параллельными;
– две прямые не лежат в одной плоскости и, следовательно, не имеют общих точек, тогда их называют скрещивающимися.
Две скрещивающиеся прямые не образуют угла в обычном понимании, потому что у них нет общей точки.
Условились считать, что угол между двумя скрещивающимися прямыми равняется углу, образованному двумя лучами, выходящимииз одной точки и параллельными этим скрещивающимсяпрямым.
ПРИМЕР;
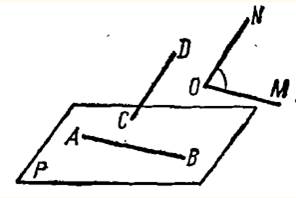
На рисунку прямые АВ и СD – скрещивающиеся, а лучи ОМ ∥ АВ и ОN ∥ СD; угол между мимолетными прямыми считают таким, который равняется углу МОN.
Расстоянием между двумя параллельными прямыми считают длину заключенного между ними отрезка прямой, перпендикулярной к каждой из параллельных прямых и пересекающей их.
Расстояние между скрещивающимися прямыми измеряется длиной отрезка прямой, перпендикулярной к каждой из скрещивающихся прямых и пересекающей каждую из них в точках, являющихся концами этого отрезка. Расстояние между двумя скрещивающимися прямыми есть наименьшее расстояние между точками, лежащими на этих прямых.
ПРИМЕР:
На рисунку изображены скрещивающиеся прямые.
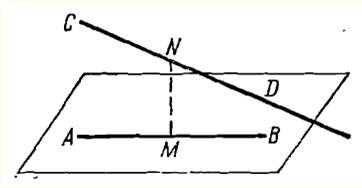
АВ, лежащая в плоскости Р, и СD, пересекающая эту плоскость. Прямая МN перпендикулярна как к АВ, так и к СD. Тогда длина отрезка МN есть расстояние между скрещивающимися прямыми АВ и СD.