План.
1. Общая схема метода разделения переменных. Понятие задачи Штурма-Лиувилля.
2. Задача Штурма-Лиувилля для отрезка, прямоугольника, прямоугольного параллелепипеда.
3. Задача Штурма-Лиувилля для круга, кругового кольца, кругового сектора, цилиндра.
4. Задача Штурма-Лиувилля для шара и шарового слоя.
5. Решение неоднородных уравнений.
1. Метод разделения переменных или метод Фурье является одним из наиболее распространенных методов решения линейных дифференциальных уравнений в частных производных. Рассмотрим общую схему этого метода на примере задачи о колебаниях струны, закрепленной на концах.
Отметим, что используемый метод может применяться и при решении других линейных уравнений математической физики.
Будем искать решение уравнения
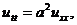 (3.1)
(3.1)
удовлетворяющее однородным граничным условиям
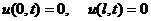 (3.2)
(3.2)
и начальным условиям
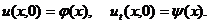 (3.3)
(3.3)
Уравнение (3.1) линейно и однородно. Поэтому сумма частных решений этого уравнения также является его решением. Найдем частное решение уравнения (3.1), удовлетворяющее граничным условиям (3.2). Представим частное решение в виде произведения
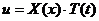 , (3.4)
, (3.4)
где 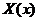 - функция только переменного
- функция только переменного 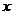 , а
, а 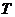 - функция только
- функция только 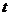 . Подставляя (3.4) в (3.1), имеем:
. Подставляя (3.4) в (3.1), имеем:
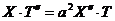 .
.
Поделим последнее уравнение на 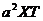 :
:
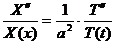 (3.5)
(3.5)
По условию переменные 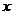 и
и 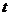 независимы. В левой части равенства находится функция только от
независимы. В левой части равенства находится функция только от 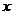 , а в правой – только
, а в правой – только 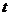 . Фиксируя, например, некоторое значение
. Фиксируя, например, некоторое значение 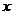 и меняя
и меняя 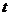 (или наоборот), получим, что правая и левая части равенства (3.5) при изменении своих аргументов сохраняют постоянное значение
(или наоборот), получим, что правая и левая части равенства (3.5) при изменении своих аргументов сохраняют постоянное значение
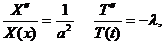 (3.6)
(3.6)
где 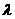 - некоторая произвольная постоянная. Знак «минус» в (3.6) использован для удобства (постоянная
- некоторая произвольная постоянная. Знак «минус» в (3.6) использован для удобства (постоянная 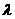 может иметь любой знак, поэтому значение выражения (3.6) не изменяется).
может иметь любой знак, поэтому значение выражения (3.6) не изменяется).
Уравнение (3.6) равносильно системе двух обыкновенных дифференциальных уравнений.
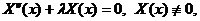 (3.7)
(3.7)
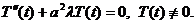 (3.8)
(3.8)
Подставляя (3.4) в граничные условия, получим:
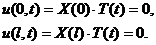
В силу нетождественности 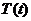 нулю, из граничных условий следует:
нулю, из граничных условий следует:
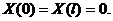 (3.9)
(3.9)
Уравнение (3.7) вместе с граничными условиями (3.9) образуют задачу о собственных значениях:
Найти те значения параметра 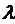 , при которых существуют нетривиальные решения задачи
, при которых существуют нетривиальные решения задачи
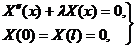 (3.10)
(3.10)
а также найти эти решения.
Значения 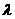 , удовлетворяющие (3.10), называются собственными значениями, а соответствующие им решения – собственными функциями. Краевая задача (3.10) называется задачей Штурма-Лиувилля для отрезка.
, удовлетворяющие (3.10), называются собственными значениями, а соответствующие им решения – собственными функциями. Краевая задача (3.10) называется задачей Штурма-Лиувилля для отрезка.
Перечислим основные свойства собственных значений и собственных функций:
1. Существует бесконечное множество собственных значений  и собственных функций
и собственных функций 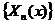 ; собственные значения при увеличении номера
; собственные значения при увеличении номера 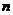 неограниченно возрастают. Каждому собственному значению соответствует конечное число линейно независимых функций.
неограниченно возрастают. Каждому собственному значению соответствует конечное число линейно независимых функций.
2. Собственные функции ортогональны между собой в области определения 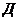 с весом
с весом 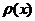 :
:
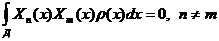 (3.11)
(3.11)
3. Теорема разложимости Стеклова. Производная дважды непрерывно дифференцируемая функция 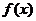 , удовлетворяющая однородному граничному условию, разлагается в абсолютно и равномерно сходящийся ряд по собственным функциям данной краевой задачи:
, удовлетворяющая однородному граничному условию, разлагается в абсолютно и равномерно сходящийся ряд по собственным функциям данной краевой задачи:
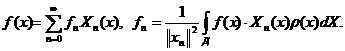 (3.12)
(3.12)
В общем случае решения с помощью метода Фурье произвольной краевой задачи для уравнения в частных производных под 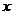 понимают совокупность переменных.
понимают совокупность переменных.
Решим задачу Штурма-Лиувилля (3.10). Отдельно рассмотрим случаи, когда параметр 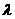 положителен, отрицателен или равен нулю.
положителен, отрицателен или равен нулю.
1. Пусть 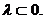 Решение уравнения (3.7) имеет вид:
Решение уравнения (3.7) имеет вид:
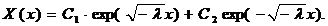
Подставляя полученное соотношение в граничные условия (3.9), имеем:
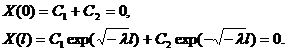 (3.13)
(3.13)
Определитель, составленный из коэффициентов при 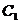 и
и 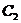 , отличен от нуля, т.е. система уравнений (3.13) имеет единственное решение:
, отличен от нуля, т.е. система уравнений (3.13) имеет единственное решение:
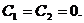
Таким образом, при 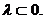 уравнение (3.7) имеет тривиальное решение.
уравнение (3.7) имеет тривиальное решение.
2. При 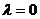 решение уравнения (3.7) имеет вид:
решение уравнения (3.7) имеет вид:
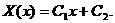
Подстановка последнего выражения в (3.9) приводит к системе уравнений для коэффициентов 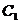 и
и 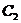 :
:

Определитель этой системы равен 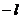 , т.е. также отличен от нуля. Таким образом уравнение (3.7) при
, т.е. также отличен от нуля. Таким образом уравнение (3.7) при 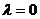 также имеет тривиальное решение.
также имеет тривиальное решение.
3. Рассмотрим случай 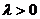 . Общее решение уравнения (3.7) имеет в этом случае вид:
. Общее решение уравнения (3.7) имеет в этом случае вид:
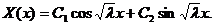 (3.14)
(3.14)
Подставляя (3.14) в граничные условия, имеем:
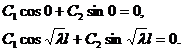 (3.15)
(3.15)
Из первого уравнения системы (3.15) следует:
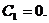
Тогда второе уравнение этой системы принимает вид:
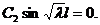
Возможны два решения последнего уравнения:
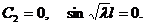
В первом случае мы получаем тривиальное решение для 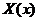 . Поэтому рассмотрим уравнение
. Поэтому рассмотрим уравнение
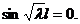
Его решение имеет вид
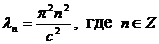 (3.16)
(3.16)
Выражение (3.16) определяет собственные значения задачи Штурма-Лиувилля. Собственные функции этой задачи имеют вид:
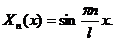 (3.17)
(3.17)
Заметим, что собственные функции задачи Штурма-Лиувилля определяются с точностью до произвольного постоянного множителя.
Рассмотрим теперь уравнение (3.8) для 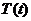 . Заметим, что отдельную задачу для
. Заметим, что отдельную задачу для 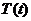 мы построить не можем, так как начальные условия (3.3) не являются однородными. Итак,
мы построить не можем, так как начальные условия (3.3) не являются однородными. Итак,
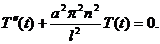 (3.18)
(3.18)
Решения уравнения (3.18) имеют вид:
 (3.19)
(3.19)
где 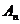 и
и 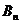 - постоянные коэффициенты.
- постоянные коэффициенты.
Подставляя (3.17) и (3.19) в (3.4), получим
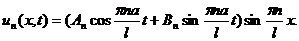 (3.20)
(3.20)
Функции 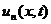 являются частными решениями уравнения (3.1), удовлетворяющими граничным условиям (3.2). Общее решение представляется в виде суммы частных решений:
являются частными решениями уравнения (3.1), удовлетворяющими граничным условиям (3.2). Общее решение представляется в виде суммы частных решений:
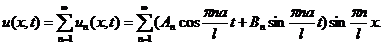 (3.21)
(3.21)
Определим неизвестные пока коэффициенты 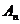 и
и 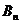 из начальных условий.
из начальных условий.
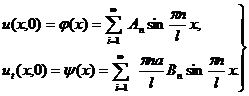 (3.22)
(3.22)
Выражения (3.22) представляют собой разложения функций 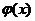 и
и 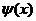 в ряд Фурье по синусам. Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция
в ряд Фурье по синусам. Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция 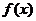 , заданная в интервале
, заданная в интервале 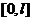 , разлагается в ряд Фурье
, разлагается в ряд Фурье
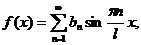
где 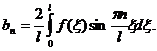
Сравнивая выражение для коэффициентов ряда Фурье и соотношениями (3.22), получим
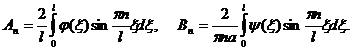 (3.23)
(3.23)
Таким образом, выражение (3.21), коэффициенты 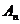 и
и 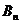 которого определяются согласно (3.23), является общим решением краевой задачи (3.1) – (3ю3) для колебаний струны.
которого определяются согласно (3.23), является общим решением краевой задачи (3.1) – (3ю3) для колебаний струны.
В заключение перечислим еще раз основные этапы решения краевой задачи с помощью метода Фурье:
1) Представить искомое решение в виде произведения двух функций:
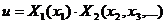 (3.24)
(3.24)
и разделить переменные.
Разделение переменных во избежание ошибки целесообразно осуществлять последовательно, отделяя, в первую очередь, те переменные, которые входят в неоднородные начальные или граничные условия.
2) Полученная в результате разделения переменных задача для функции 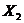 будет являться задачей Штурма-Лиувилля. Для ее решения также можно воспользоваться также расчетной схемой метода разделения переменных.
будет являться задачей Штурма-Лиувилля. Для ее решения также можно воспользоваться также расчетной схемой метода разделения переменных.
3) Решить задачу Штурма-Лиувилля для функции 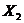 . В результате будут получены собственные функции
. В результате будут получены собственные функции 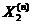 и собственные значения
и собственные значения 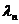 .
.
Если 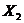 представляет собой функцию нескольких переменных, то вместо
представляет собой функцию нескольких переменных, то вместо 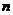 может использоваться несколько индексов, по каждому из которых в последующем будет производиться суммирование.
может использоваться несколько индексов, по каждому из которых в последующем будет производиться суммирование.
4) С учетом известных собственных значений 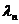 задачи Штурма-Лиувилля найти систему частных решений
задачи Штурма-Лиувилля найти систему частных решений 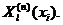
5) Представить искомое решение в виде ряда:
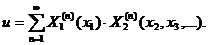 (3.25)
(3.25)
Если вместо 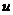 используется несколько индексов, суммирование производится по каждому из них.
используется несколько индексов, суммирование производится по каждому из них.
Коэффициенты ряда (3.25) находятся как коэффициенты разложения функций, входящих в неоднородные начальные или граничные условия по системе ортогональных функций 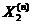 , являющихся решением задачи Штурма-Лиувилля.
, являющихся решением задачи Штурма-Лиувилля.
2. Как было отмечено выше, важную роль в решении дифференциального уравнения в частных производных методом разделения переменных играет задача Штурма-Лиувилля. В наиболее общей постановке задача Штурма-Лиувилля для оператора Лапласа имеет вид:
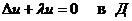 (3.26)
(3.26)
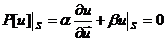 (3.27)
(3.27)
Здесь 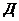 - область определения уравнения (3.26),
- область определения уравнения (3.26), 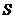 - граница области
- граница области 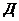 , коэффициенты
, коэффициенты 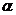 и
и 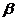 не равны нулю одновременно:
не равны нулю одновременно: 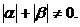
Рассмотрим методы решения задачи Штурма-Лиувилля для областей различной геометрической формы.
1) Задача Штурма-Лиувилля для отрезка.
Частный случай этой задачи рассмотрен выше. Рассмотрим ее общую постановку. Найти собственные функции уравнения
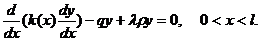 (3.28)
(3.28)
и собственные значения 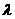 при следующих граничных условиях:
при следующих граничных условиях:
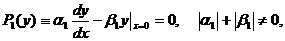 (3.29а)
(3.29а)
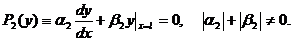 (3.29б)
(3.29б)
Знак «минус» в (3.29а) связан с тем, что внешняя нормаль к границе 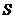 для отрезка при
для отрезка при 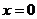 направлена в отрицательную сторону.
направлена в отрицательную сторону.
Обозначим через 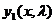 и
и 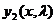 фундаментальную систему решений уравнений (3.28). Общее решение имеет вид:
фундаментальную систему решений уравнений (3.28). Общее решение имеет вид:
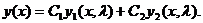 (3.30)
(3.30)
Подставим решение (3.30) в граничные условия (3.29):
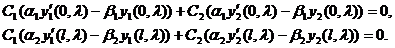 (3.31)
(3.31)
Выражение (3.31) можно рассматривать как систему алгебраических уравнений относительно неизвестных 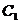 и
и 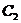 . В случае, если эта система имеет единственное решение, оно равно:
. В случае, если эта система имеет единственное решение, оно равно: 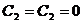 . Это решение является тривиальным и не представляет никакого интереса с физической точки зрения. По этой причине потребуем, чтобы система (3.31) имела множество решений. Это возможно в том случае, если определитель, составленный из коэффициентов системы (3.31), был равен нулю:
. Это решение является тривиальным и не представляет никакого интереса с физической точки зрения. По этой причине потребуем, чтобы система (3.31) имела множество решений. Это возможно в том случае, если определитель, составленный из коэффициентов системы (3.31), был равен нулю:
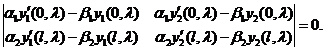 (3.32)
(3.32)
Уравнение (3.32) записано относительно 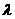 и называется дисперсным уравнением. Система решений
и называется дисперсным уравнением. Система решений  уравнения (3.32) образует спектр собственных значений задачи Штурма-Лиувилля.
уравнения (3.32) образует спектр собственных значений задачи Штурма-Лиувилля.
Найдем собственные функции задачи Штурма-Лиувилля. В силу равенства нулю определителя (3.32) уравнения системы (3.31) являются равносильными. Выберем, например, первое уравнение системы (3.31). Его решение имеет вид:
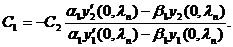
Подставляя полученный результат в (3.30), имеем:
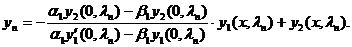 (3.33)
(3.33)
Функция (3.33) является собственной функцией задачи Штурма-Лиувилля для отрезка. Напомним, что собственные функции определяются с точностью до постоянного коэффициента, значение которого находится отдельно.
Важным частным случаем является задача Штурма-Лиувилля для отрезка 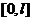 с периодическими граничными условиями. Рассмотрим задачу
с периодическими граничными условиями. Рассмотрим задачу
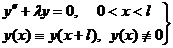 (3.34)
(3.34)
Общее решение уравнения имеет вид:
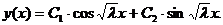
Периодичность связана с периодичностью функций синуса и косинуса. Это возможно в том случае, если
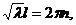
отсюда
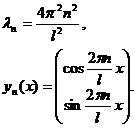 (3.35)
(3.35)
2) Задача Штурма-Лиувилля для прямоугольника.
Найти собственные функции уравнения
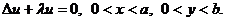 (3.36)
(3.36)
с граничными условиями
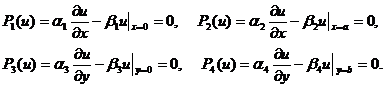 (3.37)
(3.37)
Здесь 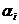 и
и  - постоянные, причем
- постоянные, причем 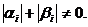
Для решения задачи (3.36) – (3.37) воспользуемся методом разделения переменных. Представим функцию 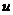 в виде произведения:
в виде произведения:
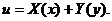 (3.38)
(3.38)
Подставляя (3.38) и выполняя преобразования, запишем:
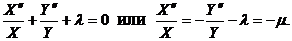 (3.39)
(3.39)
Граничные условия (3.37) принимают вид:
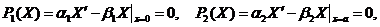 (3.40а)
(3.40а)
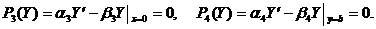 (3.40б)
(3.40б)
Соотношения (3.39) – (3.40) можно рассматривать как две задачи Штурма-Лиувилля для отрезка.
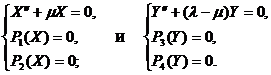 (3.41)
(3.41)
Тогда собственные значения 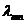 задачи Штурма-Лиувилля для прямоугольника есть сумма собственных значений
задачи Штурма-Лиувилля для прямоугольника есть сумма собственных значений 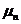 и
и 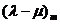 соответствующих задач для отрезка, собственная функция задачи Штурма-Лиувилля для прямоугольника есть произведения соответствующих собственных функций для отрезка:
соответствующих задач для отрезка, собственная функция задачи Штурма-Лиувилля для прямоугольника есть произведения соответствующих собственных функций для отрезка:
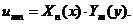 (3.42)
(3.42)
3) Задача Штурма-Лиувилля для прямоугольного параллелепипеда. Найти решение уравнения
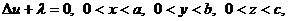 (3.43)
(3.43)
с граничными условиями
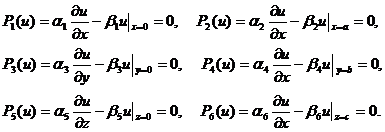 (3.44)
(3.44)
После первого разделения переменных задача (3.43) – (3.44) сведется к задачам Штурма-Лиувилля для отрезка и прямоугольника, рассмотренным выше.
Собственные функции и собственные значения задачи для прямоугольного параллелепипеда имеют вид
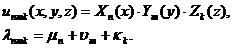 (3.45)
(3.45)
Здесь 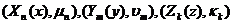 - собственные функции и собственные значения соответствующих одномерных задач Штурма-Лиувилля по каждой переменной.
- собственные функции и собственные значения соответствующих одномерных задач Штурма-Лиувилля по каждой переменной.