Понятие отношения делимости
Определение. Число а делится на число в тогда и только тогда, когда существует такое число q, что а = в × q. а  в
в  (
( q
q  N0) [а = вq].
N0) [а = вq].
Обозначают: а  в. Читают: «число а кратно числу в», «число в – делитель числа а», «а кратно в».
в. Читают: «число а кратно числу в», «число в – делитель числа а», «а кратно в».
Равенство а=вq называют формулой кратности числа а числу в.
Число а, кратное 2, называют четным. Общий вид четного числа: а = 2n, n  N0.
N0.
Число, кратное 3 имеет формулу: а = 3n, n  N0.
N0.
Определение. Отношение делимости на множестве N0  N содержит те и только те пары чисел (а, в), у которых первая координата кратна второй. Обозначают: «
N содержит те и только те пары чисел (а, в), у которых первая координата кратна второй. Обозначают: « ».
».
« » = {(а, в)| (а, в)
» = {(а, в)| (а, в)  N0
N0  N
N 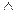 а
а  в}.
в}.
Если отношение делимости обозначить  , то
, то 
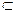 N0
N0  N
N 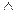
 ={(а, в)| (а, в)
={(а, в)| (а, в)  N0
N0  N
N 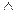 а=вq}.
а=вq}.
Теорема. Делитель в данного числа а не превышает этого числа, то есть, если а  в
в  в
в  а.
а.
Доказательство. Так как а  в, то (
в, то ( q
q  N0) [а = вq]
N0) [а = вq]  а – в=вq-в=в(q – 1), так как q
а – в=вq-в=в(q – 1), так как q  N
N  q
q  1.
1.
Тогда в (q – 1)  0
0  в
в  а. Из определения отношения делимости и равенства а = 1 × а, следует, что 1 является делителем для любого натурального числа.
а. Из определения отношения делимости и равенства а = 1 × а, следует, что 1 является делителем для любого натурального числа.
Следствие. Множество делителей данного числа конечно.
Например, делители числа 18 является конечное множество: {1, 2, 3, 6, 9, 18}.
Свойства отношения делимости
1. Отношение делимости рефлексивно, то есть любое натуральное число делится само на себя: ( а
а  N) [(а,а)
N) [(а,а) 
 ], то есть а: а = 1.
], то есть а: а = 1.
Доказательство. ( а
а  N)[а = а × 1]
N)[а = а × 1]  по определению отношения делимости а: а.
по определению отношения делимости а: а.
2. Отношение делимости антисимметрично, то есть для различных чисел а и в из того, что а 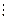 в, следует, что в не кратно а. (
в, следует, что в не кратно а. ( а, в
а, в  N0
N0  N)[а
N)[а  в
в 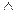 а
а 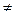 в
в 
 ].
].
Доказательство. Допустим, что в 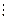 а, тогда в
а, тогда в  а. Но по условию а
а. Но по условию а  в, так как а
в, так как а  в.
в.
Неравенства в  а
а 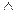 а
а  в истины только в том случае, если а = в. пришли к противоречию с условием. Следовательно, допущение, что в
в истины только в том случае, если а = в. пришли к противоречию с условием. Следовательно, допущение, что в 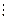 а
а 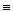 Л. Таким образом, отношение делимости антисимметрично.
Л. Таким образом, отношение делимости антисимметрично.
3. Отношение делимости транзитивно. ( а,в,с
а,в,с  N0
N0  N)[а
N)[а  в
в 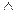 в
в  с
с  а
а  с].
с].
Доказательство. Если а  в
в  (
( q
q  N)[а = вq] (1) Из того, что в
N)[а = вq] (1) Из того, что в  с
с  (
( t
t  N)[в = сt] (2)
N)[в = сt] (2)
Подставим в = сt в равенство (1), получим: а = (сt)q = c(tq), t,q  N
N  tq
tq  N
N  tq = р
tq = р  а = ср, р
а = ср, р  N. А это значит, что а
N. А это значит, что а  с.
с.
Признаки делимости. Делимость суммы, разности, произведения
Определение. Признаком делимости называется предложение, в котором доказывается как можно предсказать делимость одного числа на другое, не выполняя деления этих чисел.
Теорема (признак делимости суммы). Если числа а и в делится на число n, то их сумма делится на это число, ( а,в, n
а,в, n  N0
N0  N)[а
N)[а  n
n 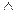 в
в  n
n  (а + в)
(а + в)  n].
n].
Доказательство. Из того что а  n
n 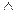 в
в  n (по определению отношения делимости)
n (по определению отношения делимости) 
 а=nq1 (1), q1
а=nq1 (1), q1  N. в=nq2 (2), q2
N. в=nq2 (2), q2  N. Преобразуем сумму (а + в) к виду:
N. Преобразуем сумму (а + в) к виду:
а + в = nq1 + nq2 = n (q1 + q2) = nq,q = q1 + q2.  а + в = nq.
а + в = nq.
Следовательно, по определению отношения делимости, что (а + в)  n.
n.
Теорема (признак делимости разности). Если числа а и в делятся на число n и а  в, то их разность а – в делится на число n, то есть
в, то их разность а – в делится на число n, то есть
( а,в,n
а,в,n  N0
N0  N)[а
N)[а  n
n 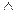 в
в  n
n 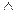 а
а  в
в  (а – в)
(а – в)  n].
n].
Теорема (признак делимости произведения). Если один из множителей произведения делится на число n, то и все произведение делится на число n.
( а,в,n
а,в,n  N0
N0  N)[а
N)[а  n
n  (ав)
(ав)  n].
n].
Доказательство. Из того, что а  n
n  а = nq (1). Умножим обе части равенства (1) на в
а = nq (1). Умножим обе части равенства (1) на в  N, получим: ав = nqв
N, получим: ав = nqв  (по ассоциативности умножения) ав = n(qв) = nt, где t = qв
(по ассоциативности умножения) ав = n(qв) = nt, где t = qв  ав = nt. А это значит, что ав
ав = nt. А это значит, что ав  n (по определению отношения делимости). Таким образом, для делимости произведения на число достаточно чтобы на данное число делился хотя бы один из множителей этого произведения.
n (по определению отношения делимости). Таким образом, для делимости произведения на число достаточно чтобы на данное число делился хотя бы один из множителей этого произведения.
Теорема. Если в произведении ав множитель а делится на натуральное число m, а множитель в делится на натуральное число n, то ав делится на mn.
( а,в,m,n
а,в,m,n  N)[а
N)[а  m
m 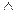 в
в  n
n  ав
ав  mn].
mn].
Доказательство. Из того, что а  m
m  а = mq1, q1
а = mq1, q1  N; в
N; в  n
n  в = nq2, q2
в = nq2, q2  N
N 
 ав = mq1 × nq2, = mn(q1 × q2) = mnq, q1 × q2 = q
ав = mq1 × nq2, = mn(q1 × q2) = mnq, q1 × q2 = q  N.
N.  ав = mnq
ав = mnq  ав
ав  mn.
mn.
Теорема (признак делимости на 2). Для того, чтобы число х делилось на 2 необходимо и достаточно, чтобы его десятичная запись оканчивалась одной из цифр: 0, 2, 4, 6, 8.
Доказательство. Пусть число х записано в десятичной системе счисления, то есть:
х = аn10n + an–110n–1 + …+a110 + a0, где аn, an–1, …, а1 – цифры, принимающие значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и аn 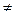 0, а0 – принимает значения 0, 2, 4, 6, 8.
0, а0 – принимает значения 0, 2, 4, 6, 8.
 Докажем, что число х
Докажем, что число х  2. Так как 10
2. Так как 10  2, то любая степень числа 10
2, то любая степень числа 10  2. Десятичную запись числа х представим в виде: х = (аn10n + an–110n–1 + …+a110) + a0
2. Десятичную запись числа х представим в виде: х = (аn10n + an–110n–1 + …+a110) + a0
I слагаемое II слагаемое
В этой сумме первое слагаемое по признаку делимости суммы делится на 2. Второе слагаемое а0  2 (по условию). Следовательно, по признаку делимости суммы на число х делится на 2.
2 (по условию). Следовательно, по признаку делимости суммы на число х делится на 2.
Обратно, если число х делится на 2, то его десятичная запись оканчивается цифрой 0, 2, 4, 6, 8.
Запишем число х = аn10n + an–110n–1 + …+a110 + a0 в виде: а0 = х – (аn10n + an–110n–1 + …+a110).
В этой разности число х  2 (по условию), вычитаемое (аn10n + an–110n–1 + …+a110)
2 (по условию), вычитаемое (аn10n + an–110n–1 + …+a110)  2 (по признаку делимости суммы). Следовательно, по теореме о делимости разности а0
2 (по признаку делимости суммы). Следовательно, по теореме о делимости разности а0  2. Чтобы однозначное число а0 делилось на 2, оно должно принимать значения 0, 2, 4, 6, 8.
2. Чтобы однозначное число а0 делилось на 2, оно должно принимать значения 0, 2, 4, 6, 8.
Признак делимости на 2. На 2 делятся те и только те числа, в разряде единиц которых содержится число, делящееся на 2 или на 2 делятся те и только те числа, десятичная запись которых оканчивается одной из цифр 0, 2, 4, 6, 8.
Теорема (признак делимости на 5). Для того, чтобы число х делилось на 5, необходимо и достаточно, чтобы его десятичная запись оканчивалась цифрой 0 или 5.
Лемма. ( n
n  N) [n > 1
N) [n > 1  10n
10n  4].
4].
Доказательство. Так как 100 = 4 × 25, то по признаку делимости произведения
100  4. Тогда (
4. Тогда ( n
n  N
N 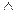 n > 1)[10n = 102 × 10n–2]
n > 1)[10n = 102 × 10n–2]  10n = 100 × 10n–2 и по признаку делимости произведения 10n
10n = 100 × 10n–2 и по признаку делимости произведения 10n  4.
4.
Теорема (признак делимости на 4). Натуральное число х делится на 4 тогда и только тогда, когда две последние цифры его десятичной записи образуют двузначное число, делящееся на 4.
Пусть х = аn10n + an–110n–1 + …+a110 + a0 и пусть десятичная запись двух последних цифр a110 + a0 выражает число  , которое делится на 4.
, которое делится на 4.
Доказательство. Представим число х в виде суммы двух слагаемых:
 х = (аn10n + an–110n–1 + …+a2102) + (а110 + а0),
х = (аn10n + an–110n–1 + …+a2102) + (а110 + а0),
I слагаемое II слагаемое
где первое слагаемое, по доказанной выше Лемме, делится на 4, второе слагаемое делится на 4 по условию. Следовательно, согласно признака делимости суммы на число, число х делится на 4.
Обратно, если число х  4, то
4, то  – двузначное число, образованное последними цифрами его десятичной записи, делится на 4.
– двузначное число, образованное последними цифрами его десятичной записи, делится на 4.
По условию х  4. Докажем, что (а110 + а0)
4. Докажем, что (а110 + а0)  4.
4.
Доказательство. Десятичная запись числа х имеет вид:
х = аn10n + an–110n–1 + …+а2 102 + a110 + a0, представим число х в виде суммы двух слагаемых:
х = (аn10n + an–110n–1 + …+a2102) + (а110 + а0) и запишем равенство в виде:
х – (аn10n + an–110n–1 + …+a2102) = а110 + а0, где х  4
4 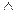 (аn10n + an–110n–1 + …+a2102)
(аn10n + an–110n–1 + …+a2102)  4 (по лемме).
4 (по лемме).
Следовательно, по признаку делимости разности а110 + а0  4. выражение а110 + а0 =
4. выражение а110 + а0 =  – есть запись двузначного числа, образованного последними цифрами записи числа х.
– есть запись двузначного числа, образованного последними цифрами записи числа х.
Признак делимости на 4. На 4 делятся те и только те числа, две последние цифры десятичной записи которых образуют число, делящееся на 4.
Теорема. Для того чтобы число х делилось на 25 необходимо и достаточно, чтобы на 25 делилось двузначное число, образованное последними двумя цифрами десятичной записи числа х.
Доказывается аналогично.
Признак делимости на 25. На 25 делятся те и только те числа, у которых две последние цифры в записи числа 00, 25, 50, 75.
Лемма. ( n
n  N) [(10n – 1)
N) [(10n – 1)  9].
9].
Докажем методом математической индукции.
1. Проверим справедливость утверждения для n = 1,
имеем: 101 – 1 = 9  9
9  9.
9.  А(1)
А(1) 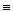 И.
И.
2. Допустим, что утверждение справедливо для n = k,
имеем: 10k – 1  9
9  А(k)
А(k) 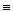 И – индукционное допущение.
И – индукционное допущение.
1. Докажем справедливость утверждения для n = k + 1, имеем:
2. 10k+ 1 – 1 = 10k × 10 – 1 = 10k (9 + 1) – 1 = 10k × 9 + 10k × 1 – 1 = 10k × 9 + 10k – 1, где первое слагаемое 10k × 9  9 (по признаку делимости произведения), второе слагаемое 10k – 1
9 (по признаку делимости произведения), второе слагаемое 10k – 1  9 (по допущению индукции). Следовательно, по признаку делимости суммы вся сумма делится на 9.
9 (по допущению индукции). Следовательно, по признаку делимости суммы вся сумма делится на 9.
Таким образом, А (1) 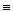 И
И 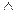 А(k)
А(k) 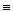 И
И  А(k + 1)
А(k + 1) 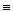 И.
И.
Следовательно, лемма доказана, то есть (10n – 1)  9.
9.
Теорема (признак делимости на 9). Для того чтобы число х делилось на 9, необходимо и достаточно, чтобы сумма цифр его десятичной записи делалась на 9.
Пусть х = аn10n + an–110n–1 + …+a110 + a0 (1), где где аn, an–1, …, а1, а0 – цифры, принимающие значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и аn 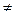 0 и (аn + an–1 + … + а1 + а0)
0 и (аn + an–1 + … + а1 + а0)  9.
9.
Докажем, что число х  9. Доказательство. Преобразуем сумму (1), прибавив и вычтя из нее выражение аn + an–1 + … + а1 + а0, получим:
9. Доказательство. Преобразуем сумму (1), прибавив и вычтя из нее выражение аn + an–1 + … + а1 + а0, получим:
х = аn10n + an–110n–1 + …+a110 + a0 + аn – an + an – 1 – an – 1 + …+ a1 – a1 + a0 – a0 =
= (аn10n – an) + (an–110n–1 – an – 1) + … + (a110 – a1) + (a0 – a0) =
=аn (10n – 1) + an–1 (10n–1 – 1) + … + a1 (10 –1) + (аn + an–1 + … + а1 + а0).
В полученной сумме каждое слагаемое делится на 9 (по признаку делимости произведения):
аn (10n – 1)  9, так как (10n – 1)
9, так как (10n – 1)  9; an–1 (10n–1 – 1)
9; an–1 (10n–1 – 1)  9, так как (10 – 1)
9, так как (10 – 1)  9; аn + an–1 + … + а1 + а0
9; аn + an–1 + … + а1 + а0  9 (по условию). Следовательно, х
9 (по условию). Следовательно, х  9.
9.
Обратно, если х  9, то сумма цифр десятичной записи числа х делится на 9.
9, то сумма цифр десятичной записи числа х делится на 9.
Равенство х = аn10n + an–110n–1 + …+a110 + a0 запишем в виде: а
аn + an–1 + … + а1 + а0 = х – (аn (10n – 1) + an–1 (10n–1 – 1) + … + a1 (10 –1)).
Так как х  9 (по условию) и вычитаемое (аn (10n – 1) + an–1 (10n–1 – 1) + … + a1 (10 –1))
9 (по условию) и вычитаемое (аn (10n – 1) + an–1 (10n–1 – 1) + … + a1 (10 –1))  9 (по признаку делимости суммы), то по теореме о делимости разности (аn + an–1 + … + а1 + а0)
9 (по признаку делимости суммы), то по теореме о делимости разности (аn + an–1 + … + а1 + а0)  9, то есть сумма цифр десятичной записи числа х делится на 9.
9, то есть сумма цифр десятичной записи числа х делится на 9.
Лемма. ( n
n  N) [(10n – 1)
N) [(10n – 1)  3].
3].
Доказательство проведем методом математической индукции по n.
1. Проверим справедливость утверждения для n = 1,
имеем: 101 – 1 = 9  9
9  3.
3.  А(1)
А(1) 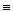 И.
И.
2. Допустим, что утверждение справедливо для n = k,
имеем: 10k – 1  3
3  А(k)
А(k) 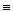 И – индукционное допущение.
И – индукционное допущение.
3. Докажем справедливость утверждения для n = k + 1, имеем: 10k+ 1 – 1 = 10k × 10 – 1 = 10k (9 + 1) – 1 = 10k × 9 + 10k × 1 – 1 = 10k × 9 + 10k – 1, где первое слагаемое 10k × 9  3 (по признаку делимости произведения), второе слагаемое 10k – 1
3 (по признаку делимости произведения), второе слагаемое 10k – 1  3 (по допущению индукции). Следовательно, по признаку делимости суммы вся сумма делится на 3.
3 (по допущению индукции). Следовательно, по признаку делимости суммы вся сумма делится на 3.
Таким образом, А (1) 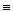 И
И 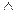 А(k)
А(k) 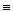 И
И  А(k + 1)
А(k + 1) 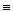 И. Следовательно, (10n – 1)
И. Следовательно, (10n – 1)  3
3
Признак делимости на 3. На 3 делятся те и только те числа, сумма цифр которых делится на 3.