Определение:
Расстоянием между двумя точками А и В является длина отрезка АВ, соединяющего эти точки.

При этом следует отметить, что точки А и В можно соединить и таким образом:
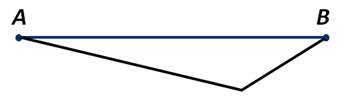
Но именно кратчайший путь, то есть отрезок АВ, является расстоянием между данными точками.
Возьмём некоторую прямую b и точку А, которая не лежит на этой прямой. Опустим перпендикуляр из точки А к прямой b:
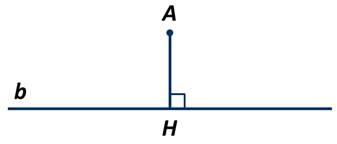
Полученный отрезок АН и будет называться расстоянием от точки А до прямой, так как это кратчайшее расстояние между данными точкой и прямой.
Действительно так. Отметим точку В на прямой b и рассмотрим прямоугольный треугольник АНВ:
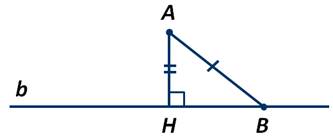
АВ - гипотенуза, а АН - катет этого треугольника. Известно, что катет всегда меньше гипотенузы.
Отрезок АВ называется наклонной, проведённой из точки А к прямой b.
Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.,
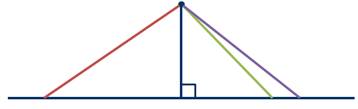
Определение:
Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой.
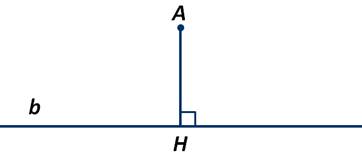
Обозначают следующим образом:
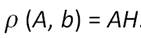
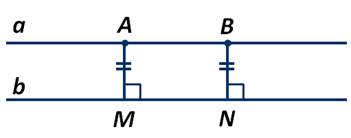
Пусть а и b - параллельные прямые. Отметим на прямой а две точки А и В и опустим из них перпендикуляры АМ и BN на прямую b:
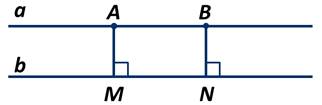
Если прямая a || b, а отрезки AM⊥ b, BN⊥ b, то АМ=BN и равняется расстоянию между параллельными прямыми а и b.
Проведём отрезок АN и рассмотрим полученные треугольники АBN и АМN:
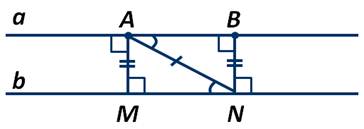
Так как AM⊥ b, а a || b, то AM⊥ a. То есть ВN⊥ b, а a || b, то и ВN⊥ a.
Получили, что АBN и АМN - прямоугольные треугольники. У них сторона АN - общая, она является гипотенузой для обоих треугольников. Углы ВАN и АNМ равны, так как являются внутренними накрест лежащими при параллельных прямых АВ и MN и секущей АN.
Следовательно, получаем, что прямоугольные треугольники АBN и АМN равны по гипотенузе и острому углу. Из этого следует, что АМ=ВN.
Получили, что отрезки АМ и BN равны.
Расстоянием между параллельными прямыми является длина их общего перпендикуляра.
Обозначают следующим образом:
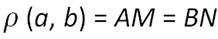
Верно и обратное утверждение:
Все точки плоскости, расположенные по одну сторону от прямой и находящиеся на равном расстоянии от неё, лежат на прямой параллельной данной.
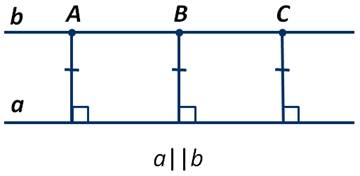
Пример.
На рисунке отрезок АВ=6 см, ∠В=30 градусов. Найти расстояние от точки А до прямой а.
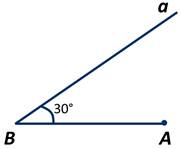
Опустим из точки А к прямой а перпендикуляр АС, который и есть расстояние от точки А до прямой а:
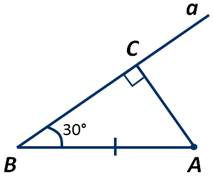
Получили прямоугольный треугольник АВС. У которого ∠В=30 градусов, АВ=6см.
Известно, что катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы. Получаем:
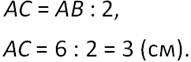
Пример.
На рисунке расстояние между параллельными прямыми а и b равно 5 сантиметров, а расстояние между параллельными прямыми а и с равно 9 сантиметров. Чему равно расстояние между параллельными прямыми b и с?

Известно, что:
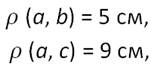
Из этого следует:
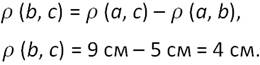
https://www.youtube.com/watch?v=UBHgFtsAVqM
https://www.youtube.com/watch?v=tpQYOm4_eHs
https://www.youtube.com/watch?v=JzeNWfukbFs
https://videouroki.net/video/25-rasstoianiie-ot-tochki-do-priamoi-rasstoianiie-miezhdu-paralliel-nymi-priamymi.html
ссылки на урок
Д/З § - 38 изучить, подготовить конспект
№ 271, 272 за 07.04.20 решить
№ 273, 274 за 09.04.20 решить