Модель точки
На рис.55, 57, 59, 61, 63 плоские изображения трехмерного объекта построены с помощью линий. Каждая линия – это множество точек, которые ограничивают линию, превращая ее в отрезок или дугу. Работая с этими изображениями, приходится выделять на линиях точки. В связи с этим необходимо знать, как строится модель точки, какие задачи нужно решать при работе с этой моделью. Поэтому рассмотрим процедуру возникновения модели точки, построенной методом двух изображений, и приемы решения задач, которые необходимо решать, работая с этой моделью.
Общий случай. Возьмём произвольную точку А трехмерного пространства и построим её модель, используя метод двух изображений (рис. 64).
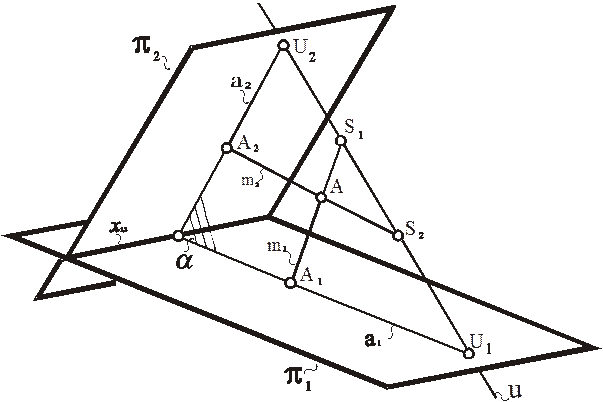
Рис. 64. Моделирование точки.
Метод двух изображений: общий случай
Алгоритм этой процедуры составят следующие операции:
1) A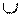 
u =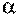 
– проецирующая плоскость;
2) α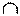 
π1= а 1 – линия связи;
3) α 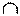π2= a 2 – линия связи;
4) А 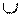S 1 = m 1 – проецирующая прямая;
5) А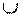 
S 2 = m 2 – проецирующая прямая;
6) m 1 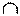а 1 = A 1 – первая проекция точки A;
7) m 2 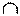a 2 = A 2 – вторая проекция точки A.
Плоскость α – плоскость в пучке проецирующих плоскостей с осью u. Прямые а 1 и а 2 называются линиями связи, а прямые m 1 и m 2 – проецирующими прямыми.
Аналогично возникают изображения любой другой точки трёхмерного пространства. Множество таких точек М, N... и исключенная прямая u порождают пучок проецирующих плоскостей (рис. 60). Эти пучки рассекаются картинами по пучкам прямых – линиям связи с вершинами в исключенных точках U 1 и U 2.
Таким образом, моделью точки трёхмерного пространства называют два её изображения (проекции), расположенные на соответствующих линиях связи.
|
|
Докажем, что такая модель является однозначной, т.е. сохраняет всю геометрическую информацию исходной точки. Такой информацией будет только положение в пространстве, так как точка не имеет ни размеров, ни формы. Для этого через центры проецирования (S 1, S 2) и изображения точки (A 1, A 2) достаточно провести проецирующие прямые, которые, пересекаясь, восстановят положение исходной точки в исходном пространстве. Кроме того, если сравнить размерность исходного и картинного пространств, то она окажется одинаковой. Действительно, на выделение одной точки из множества точек трехмерного пространства затрачивается три параметра и на выделение пары точек, которые принадлежат соответствующим лучам двух пучков, – также три параметра: один параметр тратится на то, чтобы выделить один луч в пучке прямых, другой – на выделение на этом луче проекции исходной точки, еще один параметр нужно затратить, чтобы выделить на другом луче другую проекцию точки.
Рис. 65. Моделирование точек трехмерного пространства
Исключением из этого правила окажутся точки, принадлежащие прямой u. Моделью любой точки этой прямой будут только точки U 1 и U 2. Поэтому прямая названа исключенной, а точки U 1, U 2 – исключенными.
Полученная модель, как было доказано, однозначна, но не удобна в работе, так как представляет собой громоздкую конструкцию, состоящую из двух плоскостей. Поэтому был предложен переход к однокартинному чертежу. Он заключается в перепроецировании изображений с одной картины на другую из дополнительного центра, который может совпадать с одни из заданных центров проецирования. Для каждого из частных случаев метода двух изображений, о которых будет сказано ниже, предлагается свой конкретный переход к однокартинному чертежу. Но во всех случаях возникает совмещенная картинная плоскость, каждая точка которой содержит точку обеих картин. Поэтому появилась необходимость приписывать индексы проекциям. Значения этих индексов соответствуют значению индекса той картины, которой принадлежала проекция до совмещения. При этом, после совмещения тождественно совпадают исключенные точки и линии связи. Двойные элементы, имеющие один и тот же символ, но разные индексы, помечаются двойным индексом.
|
|
В результате плоской моделью точки трехмерного пространства окажется две ее проекции, которые располагаются на двойной линии связи, проходящей через двойную исключенную точку.
Работа с моделью точки заключается в решении следующих задач:
1) построение модели любой точки трёхмерного пространства;
2) определение положения точки относительно проекционного аппарата по её модели.
В сущности решение этих задач сводится к установлению принадлежности точки к одной из групп, на которые делятся точки исходного пространства. Основанием для такой классификации служит положение точки относительно проекционного аппарата. В результате выделяются следующие группы точек:
1. Точки частного положения:
§ принадлежащие тождественной плоскости;
· принадлежащие картинам π1, π2;
· бесконечно удаленные;
· принадлежащие нейтральной плоскости.
2. Точки общего положения – все остальные.
|
|
Тождественной плоскостью называют такую, точки которой моделируются тождественно совпавшими проекциями.
Работа с моделью точки обеспечивается системой знаний, представленной в идее схемы на рис. 61. Для построения модели любой точки трехмерного пространства, необходимо знание устройства проекционного аппарата и алгоритм его работы. Для определения положения точки по отношению к проекционного аппарата необходимо умение провести процедуру обратную той, которая позволяет построить модель. Эту процедуру облегчает знание характерных признаков моделей точек частного положения.
Следует заметить, что при моделировании точек трехмерного пространства методом двух изображений мы получаем модель, которая сохраняет всю информацию исходного объекта, но пользоваться такой моделью неудобно потому, что проекции точки принадлежат двум различным плоскостям. Это обстоятельство обусловило переход к однокартинному чертежу, который осуществляется с помощью дополнительного проецирования. В различных вариантах метода двух изображений для этого выбирают различное положения дополнительного центра, но всегда проецируют из него на картину π2.
Рассмотрим решение обеих выше указанных задач на примере моделирования точек общего и частного положения в перспективе, аксонометрии и на эпюре Монжа.
Рис. 66. Знания, необходимые при работе с моделью точки
3.5.1. Моделирование точек общего положения в стандартных вариантах метода двух изображений
Перспектива.
На рис. 67 приведены пример построения модели точки трехмерного пространства в перспективе на наклонной картине с высоким горизонтом. Выводы, полученные на этом примере, справедливы для любого варианта перспективы.
Алгоритм построения модели точки такой же, как и для общего случая. Исходная точка выделяет в проецирующем пучке плоскость α, которая определяет положение линий связи а 1, а 2. Через центры проецирования и исходную точку проводят проецирующие прямые m 1, m 2. Они, пересекая соответствующие линии связи, выделяют на них проекции точки А 1, А 2.
Переход к однокартинному чертежу осуществляется благодаря перепроецированию из центра S 2 изображений с картины π 1 на картину π 2. В результате возникает еще одна проецирующая прямая m 3, которая пересекает линию связи а 2 в точке А 1. Это добавляет к алгоритму еще две операции. Чтобы различить два положения первой проекции точки А, первоначальное ее положение на картине π 1 помечают штрихом (рис. 67, 68, 69, 70).
Такой переход приводит к тому, что на картине π 2 линии связи исключенная точка оказываются двойными элементами. Алгоритм построения модели точки в перспективе с учетом перехода к однокартинному чертежу выглядит в символической записи следующим образом:
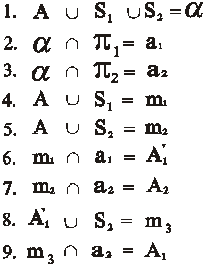
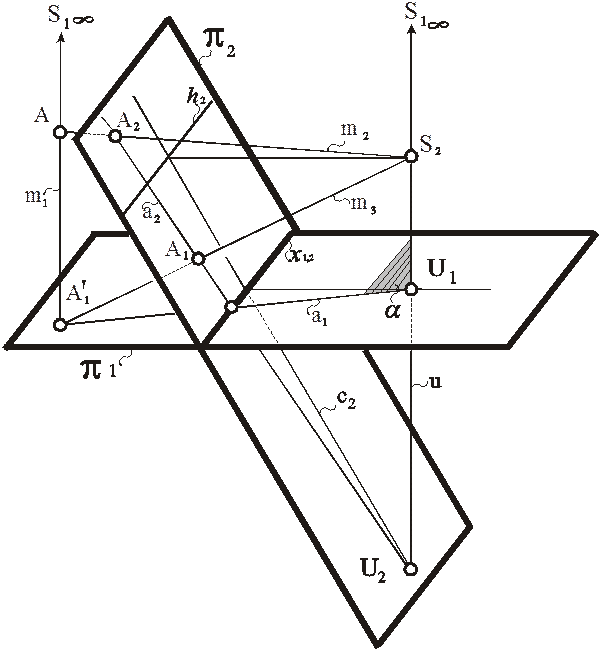
Рис. 67. Моделирование точки трехмерного пространства в перспективе
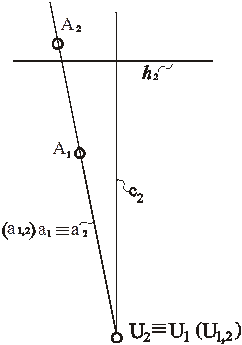
Рис. 68. Модель точки в перспективе на наклонной картине с высоким горизонтом
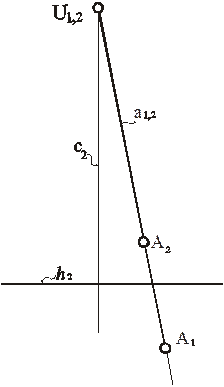
Рис. 69. Модель точки в перспективе на наклонной картине с высоким горизонтом
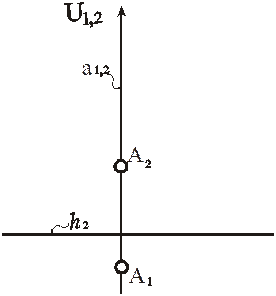
Рис. 70. Модель точки в перспективе на вертикальной картине
Аксонометрия. На рис. 71, 72 приведены пример построения модели точки трехмерного пространства в аксонометрии. Порядок операций осуществляется в соответствии со следующим алгоритмом:
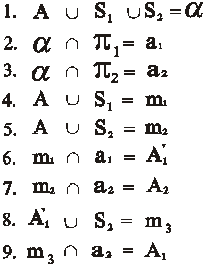
Переход к однокартинному чертежу так же как и в перспективе осуществляется благодаря перепроецированию из центра S 2 изображений с картины π 1 на картину π 2. В результате к алгоритму добавляются две операции. Возникает прямая m 3, которая пересекает линию связи а 2 в точке А 1. Чтобы различить два положения первой проекции точки А, первоначальное ее положение на картине π 1 также помечают штрихом.
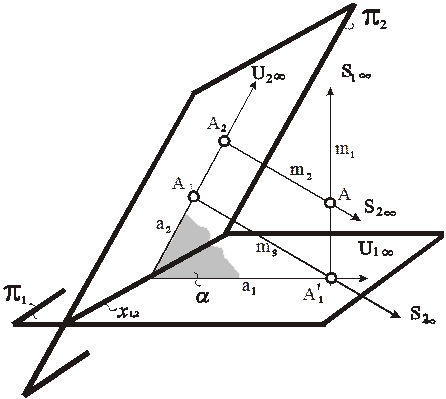
Рис. 71. Моделирование точки трехмерного пространства в аксонометрии
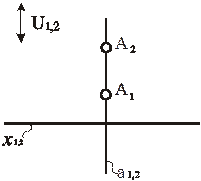
Рис. 72. Модель точки в аксонометрии
Эпюр Монжа. На рис. 73, 74 приведен пример построения модели точки трехмерного пространства на эпюре Монжа. Порядок операций осуществляется в соответствии с алгоритмом, по которому строилась модель точки в перспективе.
Только при переходе к однокартинному чертежу перепроецирование изображений с картины π 1 на картину π 2 осуществлялось из центра S 3, который удален в бесконечность под углом 45˚ к обеим картинам и принадлежит одной из биссекторных плоскостей двугранного угла, образованного обеими картинами. В результате к алгоритму также добавляются две операции. Через этот центр и А 1ʹ проходит прямая m 3, которая пересекает линию связи а 2 в точке А 1.
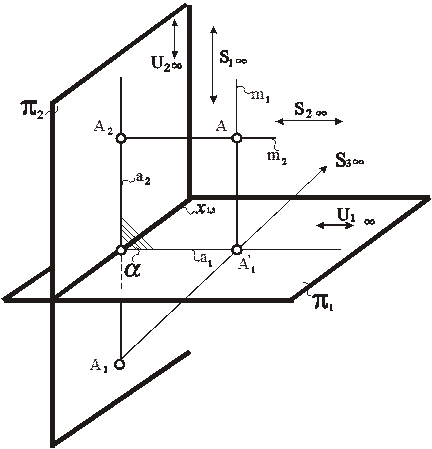
Рис. 73. Моделирование точки трехмерного пространства на эпюре Монжа
В результате получаем модель точки. Ее определение не отличается от определений в перспективе и аксонометрии: моделью точки на эпюре Монжа являются два ее изображения (проекции) на картине π2, которые принадлежат двойной линии связи пучка U 1, 2 (рис. 74).
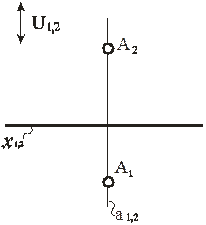
Рис. 74. Модель точки на эпюре Монжа
3.5.2. Моделирование точек частного положения в стандартных вариантах метода двух изображений
Характерный признак модели точки, принадлежащей тождественной плоскости во всех вариантах метода двух изображений один и тот же: тождественное совпадение обеих ее проекций (рис. 75, 76, 77, 78).
Роль тождественной плоскости в перспективе и аксонометрии играет картина π1. В качестве примеров приведена точка А картины π1, которая моделируется в перспективе и аксонометрии (рис. 76, 78).
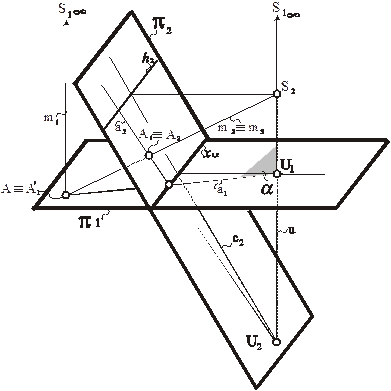
Рис. 75. Моделирование точки, принадлежащей картине π1,
в перспективе
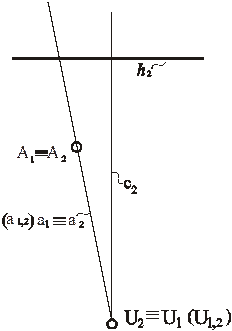
Рис. 76. Модель точки, принадлежащей картине π1, в перспективе
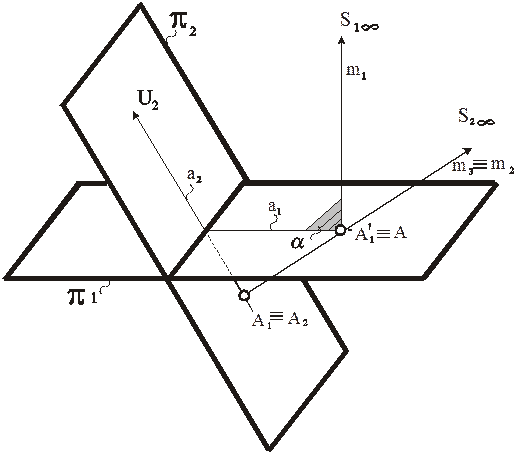
Рис. 77. Моделирование точки, принадлежащей картине π1, в аксонометрии
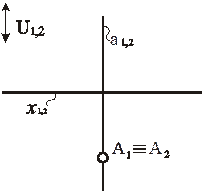
Рис. 78. Модель точки, принадлежащей картине π1, в аксонометрии
Доказательством совпадения обеих проекций точек служат не только чертежи на рис. 75и 77, но и приведенный ниже алгоритм. Он показывает, что тождественное совпадение исходной точки и ее первой проекции (А 1ʹ)приводит к тождественному совпадению проецирующих прямых m 2 и m 3. Это, в свою очередь приводит к тождественному совпадению обеих проекции точки.
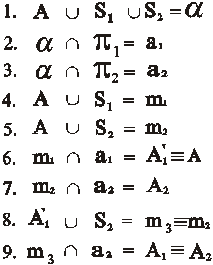
Таким образом, роль тождественной плоскости в перспективе и аксонометрии играет картина π1.
На эпюре Монжа роль тождественной плоскости играет биссекторная плоскость, которая не содержит дополнительного центра проецирования S 3. Она называется биссекторной плоскостью тождества. Процесс моделирования точки этой плоскости представлен на рис. 79. Тождественное совпадение проекций происходит после перепроецирования из центра S 3 c картины π1 на картину π2. Причиной этого совпадения является свойство точек, принадлежащих биссекторной плоскости: они равно удалены от плоскостей, которые образуют двугранный угол. В результате получаем тот же характерный признак (рис. 80), что и модели точек, принадлежащих картине π1 в перспективе и аксонометрии.
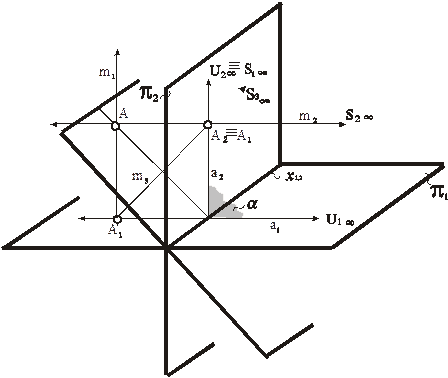
Рис. 79. Моделирование точки, принадлежащей биссекторной плоскости тождества, на эпюре Монжа
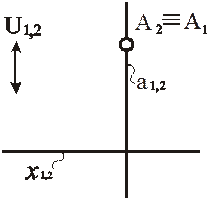
Рис. 80. Модель точки, принадлежащей биссекторной плоскости тождества, на эпюре Монжа
Характерный признак модели бесконечно удаленной точки выглядит следующим образом:
1. В аксонометрии и на эпюре Монжа обе проекции точки находятся в бесконечности.
2. В перспективе первая проекция принадлежит линии горизонта.
Приведем доказательства, опираясь на алгоритм для перспективы и эпюра Монжа.
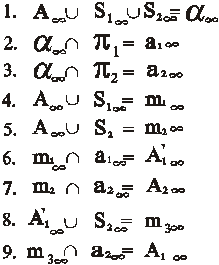
В соответствии с первой операцией алгоритма образуется бесконечно удаленную плоскость α, которая является результатом объединения трех бесконечно удаленных точек А, S 1, S 2. Это проецирующая плоскость. Она содержит все остальные элементы проецирования: линии связи, проецирующие прямые и обе проекции точки А.
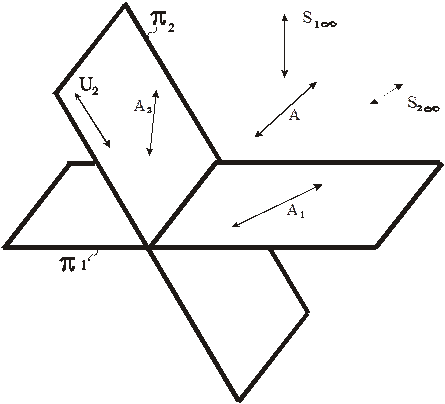
Рис. 81. Моделирование бесконечно удаленной точки в аксонометрии
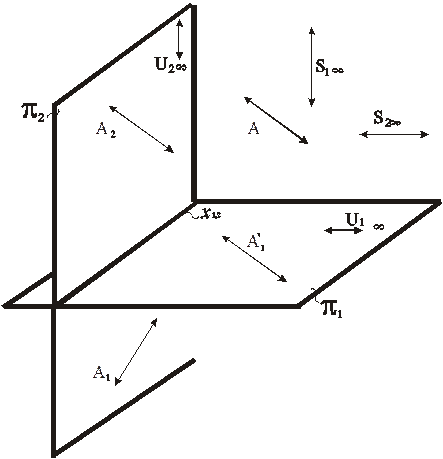
Рис. 82. Моделирование бесконечно удаленной точки на эпюре Монжа
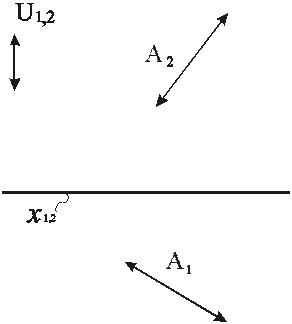
Рис. 83. Модель бесконечно удаленной точки
на эпюре Монжа и аксонометрии
В перспективе центр S 2 находится на конечном расстоянии. Это приводит к тому, что проецирующая плоскость α со всеми элементами (проецирующими прямыми, линиями связи и проекциями точки) также находится на конечном расстоянии. Исключение составляют одна проецирующая прямая m 1 и первая проекция в ее первоначальном положении. Это приводит к тому, что проецирующая прямая m 3 оказывается в плоскости горизонта и пересекает картину в точке, которая принадлежит линии горизонта h 2.
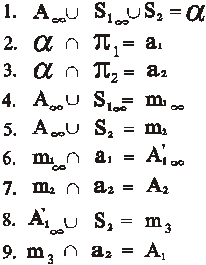
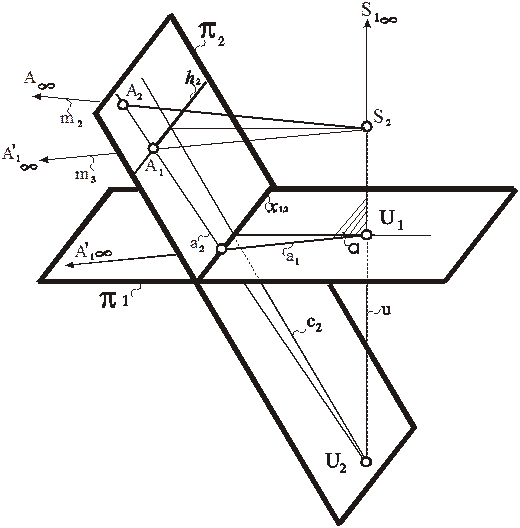
Рис. 84. Моделирование бесконечно удаленной точки в перспективе
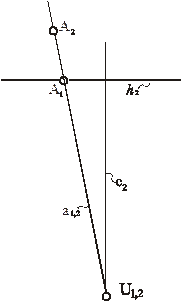
Рис. 85. Модель бесконечно удаленной точки в перспективе
Моделирование точки, принадлежащей картине π1 в перспективе и аксонометрии, уже было рассмотрено выше.
Посмотрим, какой характерный признак имеет модель точки, расположенной в картине π 1, при ее моделировании на эпюре Монжа (рис. 86, 87). Принадлежность точки к картине π1 отражается на алгоритме следующим образом: тождественно совпадают проецирующая прямая m 2 и линия связи a 1. А это, в свою очередь, является условием принадлежности второй проекции точки к оси проекций x 1,2. Таким образом, характерным признаком модели точки, которая принадлежит картине π1 на эпюре Монжа, является принадлежность второй проекции оси x 1,2.
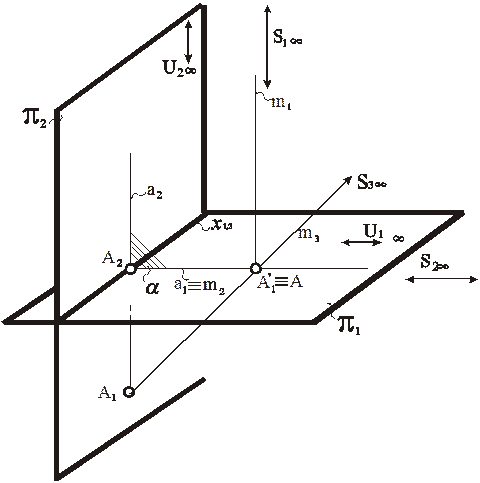
Рис. 86. Моделирование точки, принадлежащей картине π1,
на эпюре Монжа
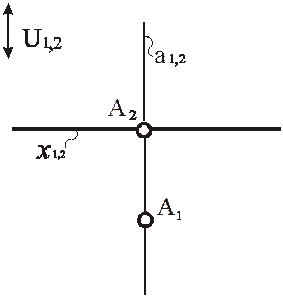
Рис. 87. Модель точки, принадлежащей картине π1
Если точка принадлежит картине π2 в перспективе на наклонной картине и аксонометрии, то ее нельзя отличить от точек общего положения. Только в перспективе на вертикальной картине она обретет отличительные черты. Характерным признаком модели точки, принадлежащей картине π2 в перспективе на вертикальной картине, является принадлежность её первой проекции основанию картины х 1,2.
Доказательством служит приведенный ниже алгоритм и рис. 88, 89. Принадлежность точки А картине π2 приводит к тождественному совпадению проецирующей прямой m 1 и линии связи a 2. В результате первая проекция точки оказывается на основании картины.
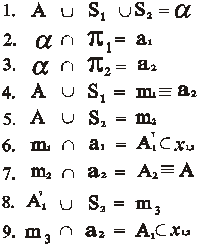
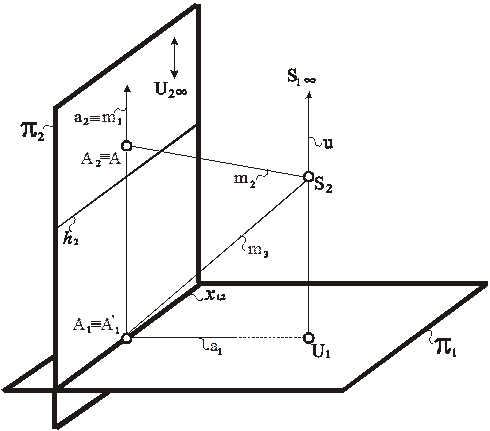
Рис. 88. Моделирование точки, принадлежащей картине π2, в перспективе
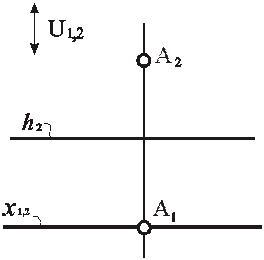
Рис. 89. Модель точки, принадлежащей картине π2,в перспективе
Выявим характерный признак модели точки, принадлежащей нейтральной плоскости. На эпюре Монжа и в аксонометрии нейтральная плоскость существует. В обоих случаях она совпадает с бесконечно удаленной плоскостью трехмерного пространства. Моделирование точек, принадлежащих этой плоскости уже рассматривалось выше. Поэтому нас будет интересовать только перспектива, где нейтральная плоскость находится на конечном расстоянии. Характерные признаки точек, принадлежащих нейтральной плоскости, в перспективе на наклонной и вертикальной картинах будут различными.
Посмотрим, как выглядит модель точки, которая принадлежит нейтральной плоскости ν, в перспективе на наклонной картине. Процесс моделирования отражен на рис. 90 и приведенном ниже алгоритме.
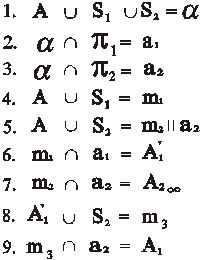
Параллельность картины π2 и плоскости ν отражается на расположении проецирующего элемента: m 2 ‖‖ a 2. Это обстоятельство приводит к тому, что общая точка этих прямых оказывается в бесконечности. Таким образом, характерным признаком модели точки, которая принадлежит нейтральной плоскости является удаление в бесконечность ее второй проекции (рис. 91).
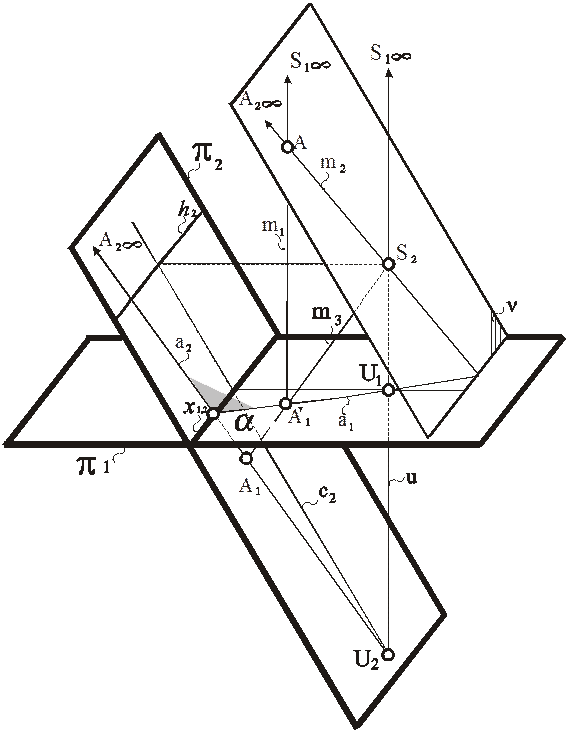
Рис. 90. Моделирование точки, принадлежащей нейтральной плоскости, в перспективе на наклонной картине
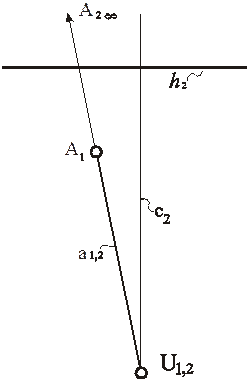
Рис. 91. Модель точки, принадлежащей нейтральной плоскости, в перспективе на наклонной картине
Если моделирование точки, которая принадлежит нейтральной плоскости ν, происходит в перспективе на вертикальной картине, то характерный признак ее модели несколько отличается от рассмотренного выше. Процесс моделирования отражен на рис. 92 и приведенном ниже алгоритме.
В этом случае происходит тождественное совпадение нейтральной плоскости ν и проецирующей плоскости α. Это обстоятельство приводит к тому, что линия связи а2 удаляется в бесконечность вместе с проекциями точки. В результате характерным признаком точки, которая лежит в нейтральной плоскости, в перспективе на вертикальной картине является удаленность в бесконечность обеих ее проекций (рис. 93).
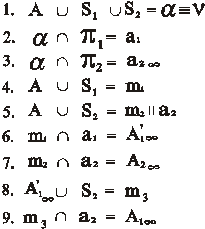
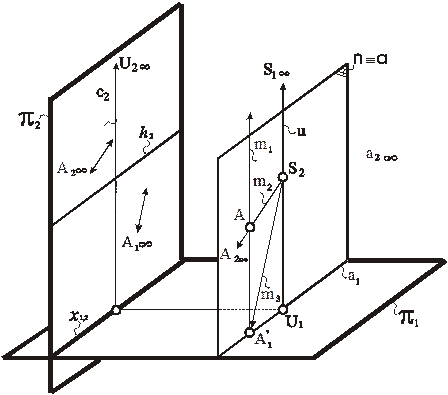
Рис. 92. Моделирование точки, принадлежащей нейтральной плоскости, в перспективе на вертикальной картине
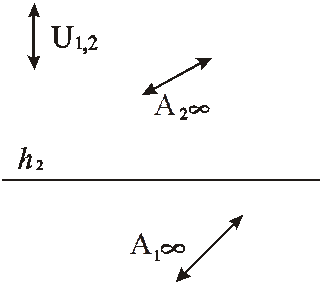
Рис. 93. Модель точки, принадлежащей нейтральной плоскости, в перспективе на вертикальной картине
Контрольные вопросы
1. Каковы операции алгоритма по построению модели точки, построенной методом двух изображений?
2. Как называется плоскость, образованная произвольной точкой трехмерного пространства и центрами проецирования?
3. линии пересечения этой плоскости с картинами?
4. Как называются прямые, проходящие через произвольную точку трехмерного пространства и центры проецирования?
5. Как называются изображения точки на картинах?
6. Дайте определение плоской модели точки трехмерного пространства, построенной методом двух изображений.
7. Приведите доказательство, что полученная модель сохраняет всю геометрическую информацию исходной точки.
8. Положение каких точек не возможно восстановить в исходном пространстве по их модели?
9. Почему необходим и как осуществляется переход к однокартинному чертежу?
10. Из решения каких задач складывается работа с моделью точки?
11. Перечислить точки, которые занимают частное положение по отношению к проекционному аппарату.
12. Какая плоскость называется тождественной в перспективе, аксонометрии, на эпюре Монжа?
13. Каков характерный признак модели точки, которая принадлежит картине p1 в перспективе, аксонометрии, на эпюре Монжа?
14. Каков характерный признак модели точки, которая принадлежит картине p2 в перспективе, аксонометрии, на эпюре Монжа?
15. Что характерного в модели точки, которая бесконечно удалена в перспективе, аксонометрии, на эпюре Монжа?
16. Чем отличается модель точки, которая принадлежит нейтральной плоскости в перспективе на наклонной и вертикальной картинах?