Расчетно-графическая работа по дисциплине «Методы анализа данных»
(задание1 – с.1, задание 2- с.20)
Задание 1 Анализ исходных данных
Выбор варианта:
| Порядковый номер по журналу | Вариант по таблице 1 |
| Значения варианта1 умножить на 1,1 | |
| Значения вариант 3 умножить на 1,1 | |
| Значения вариант 5 умножить на 1,1 | |
| Значения вариант 7 умножить на 1,1 | |
| Значения вариант 8 умножить на 1,1 | |
| Значения вариант 6 умножить на 1,1 | |
| Значения вариант 9 умножить на 1,1 | |
| Значения вариант 2 умножить на 1,1 | |
| Значения вариант 4 умножить на 1,1 | |
| Значения вариант 1 умножить на 1,2 | |
| Значения вариант 2 умножить на 1,2 | |
| Значения вариант 3 умножить на 1,2 | |
| Значения вариант 4 умножить на 1,2 | |
| Значения вариант 5 умножить на 1,2 | |
| Значения вариант 6 умножить на 1,2 |
Для каждого варианта (таблица 1) представлены выборочные значения случайной величины Х (выборка объемом n=45). Х - это результаты регистрации значений затухания сигнала xi на частоте 1000 Гц коммутируемого канала телефонной сети. Эти значения, измеренные в дБ, в виде вариационного ряда представлены в табл. 1 Необходимо построить вариационный ряд, представить его графически, проанализировать и рассчитать характеристики.
Необходимо:
1. Вычислить выборочное среднее по первым 25 значениям, вычислить выборочное среднее по всему объему выборки. Сравнить.
2. Вычислить выборочную дисперсию по первым 25 значениям, вычислить выборочную дисперсию по всему объему выборки. Сравнить.
3. Рассчитать моду и медиану вариационного ряда (n=45).
4. Получить интервальный вариационный ряд по всему объему выборки, разделив выборочные значения на 5 интервалов.
5. Построить гистограмму. Сделать вывод.
6. Рассчитать выборочное среднее, выборочную дисперсию интервального вариационного ряда, моду и медиану.
7. Рассчитать коэффициент вариации, коэффициенты асимметрии и эксцесса и сделать вывод о характере распределения случайной величины Х. Пояснить результат.
8. Построить эмпирическую функцию распределения случайной величины Х. Построить теоретическую функцию распределения случайной величины Х.
9. Проверить, включает ли выборка аномальные значения (по правилу «трех сигм»). Сделать вывод по п.7, 8, 9.
В отчете результаты выполнения представить в виде таблицы.
Распределение значений признака по диапазонам рассеяния признака относительно 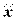
| Границы диапазонов, дБ | Количество значений xi, находящихся в диапазоне | Процентное соотношение рассеяния значений xi по диапазонам, % | ||||
| Первый признак | Первый признак | Первый признак | ||||
| А | ||||||
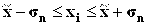
| [; ] | |||||
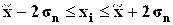
| [; ] | |||||
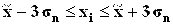
| [; ] |
9. Составить аналитическое заключение по заданию 1.
Таблица 1 – Исходные данные к заданию 1
| № | Варианты | ||||||||
| 1,19 | 1,64 | 2,66 | 4,12 | 4,53 | 5.07 | 7,57 | 8,99 | 9,97 | |
| 0,92 | 1,79 | 2,98 | 4,03 | 4,77 | 7,02 | 6,56 | 6,88 | 7,25 | |
| 0,87 | 1,63 | 3,42 | 3,92 | 5,58 | 6,50 | 6,71 | 6,48 | 8,46 | |
| 0,83 | 2,11 | 2,68 | 3,46 | 5,12 | 7,03 | 6,40 | 9,43 | 7,90 | |
| 0,98 | 2,03 | 3,09 | 4,63 | 4,74 | 5,85 | 8,20 | 8,83 | 8,03 | |
| 1,18 | 1,64 | 3,19 | 3,42 | 5,07 | 6,45 | 8,27 | 7,02 | 9,34 | |
| 1,19 | 2,03 | 2,54 | 4,44 | 5,17 | 5,65 | 8,14 | 8,89 | 10,76 | |
| 1,11 | 2,10 | 2,69 | 3,43 | 4,09 | 7,19 | 5,74 | 9,36 | 10,32 | |
| 1,18 | 2,16 | 2,83 | 3,63 | 4,85 | 6,20 | 8,29 | 8,15 | 7,60 | |
| 0,88 | 2,09 | 2,97 | 4,24 | 4,68 | 5,37 | 6,16 | 8,39 | 7,25 | |
| 0,87 | 1,81 | 3,02 | 4,55 | 5,38 | 7,14 | 6,06 | 8,23 | 10,79 | |
| 1,08 | 1,62 | 3,56 | 4,18 | 4,22 | 7,12 | 6,66 | 8,88 | 10,09 | |
| 1,04 | 2,22 | 2,64 | 3,28 | 4,09 | 4,82 | 7,73 | 8,99 | 9,98 | |
| 0,86 | 1,75 | 3,43 | 3,93 | 4,03 | 6,47 | 6,85 | 6,84 | 7,46 | |
| 1,07 | 1,81 | 2,66 | 4,38 | 5,50 | 5,41 | 8,04 | 8,97 | 8,84 | |
| 1,12 | 2,11 | 2,44 | 3,93 | 4,20 | 6,14 | 7,50 | 8,77 | 8,05 | |
| 0,93 | 1,84 | 2,70 | 3,79 | 5,35 | 6,74 | 6,84 | 9,58 | 9,84 | |
| 0,82 | 1,77 | 3,35 | 4,17 | 4,19 | 6,96 | 6,03 | 9,29 | 7,95 | |
| 1,11 | 2,21 | 3,58 | 4,80 | 4,80 | 4,85 | 6,31 | 8,53 | 10,40 | |
| 0,98 | 2,36 | 2,79 | 4,10 | 5,09 | 5,53 | 7,79 | 8,09 | 9,94 | |
| 1,09 | 2,10 | 3,43 | 3,77 | 4,33 | 5,31 | 5,83 | 6,51 | 7,96 | |
| 0,95 | 1,60 | 2,47 | 3,53 | 4,18 | 6,30 | 7,82 | 7,25 | 8,69 | |
| 0,84 | 2,29 | 2,62 | 3,39 | 5,78 | 6,55 | 6,14 | 6,99 | 7,47 | |
| 1,03 | 1,85 | 3,44 | 3,82 | 4,09 | 7,17 | 6,55 | 7,5 | 7,71 | |
| 1,17 | 2,35 | 2,48 | 3.43 | 4,34 | 5.78 | 6,91 | 6,89 | 7,24 | |
| 1,11 | 2,0 | 2,53 | 3,3 | 5,43 | 7,11 | 6,22 | 8,19 | 9,64 | |
| 0,84 | 1,93 | 3,00 | 3,35 | 5,80 | 5,30 | 6,46 | 9,27 | 9,97 | |
| 1,04 | 1,81 | 3,24 | 3,60 | 5,60 | 6,31 | 8,12 | 7,95 | 10,61 | |
| 0,86 | 2,34 | 3,19 | 4,60 | 4,29 | 5,18 | 7,95 | 7,83 | 7.30 | |
| 0,81 | 2,01 | 3,14 | 4,42 | 5,43 | 6,89 | 7,55 | 7,40 | 8,66 | |
| 1,09 | 2,20 | 2,79 | 4,65 | 5,80 | 6,48 | 7,29 | 7,90 | 8,29 | |
| 0,86 | 2,10 | 3,07 | 3,61 | 5,89 | 5,15 | 8,17 | 9,56 | 9,37 | |
| 0,94 | 2,30 | 2,82 | 3,35 | 5,87 | 6,65 | 8,08 | 6,75 | 10,43 | |
| 1,18 | 1,84 | 3,27 | 4,67 | 4,88 | 5,42 | 8,34 | 7,80 | 9,03 | |
| 1,02 | 2,28 | 2,99 | 4,67 | 5,40 | 5,89 | 7,29 | 8,85 | 7,75 | |
| 1,20 | 1,87 | 2,96 | 3,23 | 5,87 | 5,26 | 6,51 | 9,59 | 9,76 | |
| 1,04 | 2,29 | 2,71 | 3,43 | 4,46 | 5,73 | 6,89 | 7,86 | 9,04 | |
| 0,86 | 2,18 | 2,65 | 3,50 | 5,32 | 5,26 | 6,31 | 7,09 | 7,67 | |
| 1,11 | 1,68 | 3,24 | 3,90 | 4,30 | 5,78 | 5,84 | 6,83 | 10,40 | |
| 1,14 | 1,85 | 2,98 | 4,32 | 5,26 | 6,83 | 6,91 | 9,12 | 9,58 | |
| 0,97 | 2,07 | 3,36 | 3,99 | 4,83 | 6,38 | 8,07 | 6,90 | 9,01 | |
| 1,05 | 1,65 | 3,60 | 3,96 | 4,56 | 4,81 | 7,83 | 7,03 | 7,94 | |
| 1,00 | 2,27 | 3,28 | 4,78 | 4,04 | 6,40 | 7,88 | 9,25 | 7,67 | |
| 1,00 | 2,09 | 2,81 | 3,27 | 5,73 | 5,18 | 6,98 | 6,49 | 10,55 | |
| 0,88 | 2,18 | 3,18 | 3,31 | 5,10 | 5,43 | 7,56 | 7,24 | 10,27 |
Теоретическая часть к заданию 1
А. Общие сведения
Анализ данных включает три основных этапа:
1. Сбор.
2. Подготовка.
3. Обработка данных.
Данные по виду можно подразделить на числовые и категориальные.
Числовые данные (Numerical Data) – это данные, характеризующие состояние какого-либо параметра изучаемого объекта. Наиболее часто такие данные бывают представлены вещественными числами. Примерами числовых данных являются заработная плата, население страны, артериальное давление, температура воздуха.
Категориальные данные (Categorical Data) – это данные, образующие признак принадлежности к какой-либо группе. Примерами категориальных данных являются экзаменационная оценка, цвет автомобиля, уровень образования человека.
Сбор данных – процесс формирования структурированного набора данных в цифровой форме. В некоторых случаях процесс сбора данных может включать также этап оцифровки.
Как правило, оцифрованные данные бывают представлены в виде: электронных таблиц в форматах XLS либо ODS;
- текстовых файлов в формате CSV;
- веб-страниц в формате HTML;
- файлов в формате XML;
- базы данных с доступом по технологии JSON либо через специализированный интерфейс (API).
В случаях, когда источники данных структурированы и представлены в сети Интернет, возможна реализация автоматизированного сбора данных.
Для использования в системах анализа данные должны быть представлены в определенном, как правило, табличном виде. Однако зачастую наборы данных имеют следующие особенности:
- отличную от табличной форму представления;
- пропуски отдельных данных;
- некорректные значения;
- большие числовые значения;
- текстовые данные.
Перечисленные особенности могут либо привести к затруднениям в процессе дальнейшей обработки данных, либо сделать её невозможной. Для устранения отмеченных несоответствий могут быть применены следующие операции:
- структурирование – приведение данных к табличному (матричному) виду;
- отбор – исключение записей с отсутствующими или некорректными значениями;
- нормализация – приведение числовых значений к определенному диапазону, например к диапазону 0...1;
- кодирование – это представление категориальных данных в числовой форме. Например, при бинарной классификации один из классов можно представить числом «0», а другой класс – числом «1». При множественной классификации система кодирования несколько усложняется: создается несколько числовых полей по количеству классов в выборке данных, каждый класс кодируется проставлением числа «1» в соответствующем поле.
Статистические данные, как правило, представляются в виде числовых таблиц больших размеров. Если пытаться анализировать данные, просматривая таблицу, потребуются большие затраты времени и, чаще всего, целый ряд свойств данных останется не выявленным, поскольку представление информации в виде чисел лишено наглядности и не дает конкретного визуального указания о наличии этих свойств. Более информативно для анализа использование графического отображения данных построение полигона (в случае дискретного признака) или гистограммы (в случае непрерывного признака).
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1, n1), (x2, n2), …, (xk, nk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат ni. Точки (xi, ni) соединяют отрезками прямых и получают полигон частот.
1. Пример. В результате выборки получена следующая таблица распределения частот.
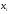
| |||
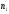
|
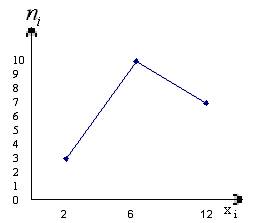
Рисунок 1 – Полигон частот
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 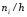 (плотность частоты).
(плотность частоты).
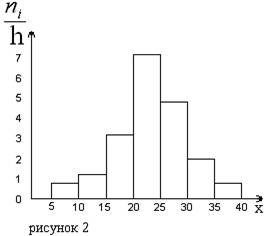
Рисунок 2 – Гистограмма частот
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на расстоянии 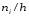 .
.
Площадь i-го частичного прямоугольника равна 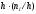 =
= 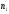 ─ сумме частот вариантi-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки n.
─ сумме частот вариантi-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки n.
На рисунке 2 изображена гистограмма частот распределения объема n=100, приведенного в таблице 2.
Таблица 2 - Вспомогательная таблица
| Частичный интервал, длиною h=5 | Сумма частот вариант частичного интервала 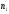
| Плотность частоты 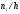
|
| 5 – 10 | 0,8 | |
| 10 – 15 | 1,2 | |
| 15 – 20 | 3,2 | |
| 20 – 25 | 7,2 | |
| 25 – 30 | 4,8 | |
| 30 – 35 | 2,0 | |
| 34 – 40 | 0,8 |
Визуальный анализ полигона или гистограммы позволяет выявить характер распределения данных и ответить на следующие шесть вопросов:
1. Какие значения типичны для заданного набора данных?
2. Как различаются между собой значения (диапазон значений)?
3. Сконцентрированы ли данные вокруг некоторого типичного значения?
4. Какой характер имеет эта концентрация данных? В частности, одинаков ли характер «затухания» для малых и больших значений данных?
5. Есть ли в заданном наборе такие значения, которые сильно отличаются от остальных и требуют специальной обработки (выбросы)? Можно ли сказать, что в целом это однородный набор или отчетливо наблюдается наличие групп, которые надо анализировать отдельно?
При анализе полигонов или гистограмм иногда в данных можно наблюдать выбросы (сильно отклоняющиеся значения), т.е. такие такие значения, которые либо слишком велики, либо слишком малы. Существуют два вида выбросов: ошибки и корректные, но «отличающиеся» значения данных.
С ошибками справиться легко они сильно отличаются от остальных значений на гистограмме. В этом случае нужно перепроверить данные, найти ошибку и исправить это значение.
Более сложной является проблема выбросов корректных данных. Если есть убедительное подтверждение того, что выбросы не соответствуют изучаемым данным, то их можно просто удалить и анализировать оставшиеся более согласованные между собой данные. При отсутствии достаточно обоснованного аргумента для исключения выбросов можно выполнить два различных анализа: один с учетом выбросов, другой – с исключением их. В лучшем случае может оказаться, что наличие выбросов не имеет существенного значения. Если два анализа дадут разные результаты, то выводы могут быть менее определенными и неоднозначными. В современной статистике в настоящее время разрабатываются устойчивые методы, в которых применяется мощный вычислительный аппарат для учета наличия выбросов.
Обычно в статистике предполагают, что распределение данных приблизительно соответствует нормальному. Это объясняется тем, что многие стандартные методы статистического анализа, например, вычисление доверительных интервалов или проверка статистических гипотез, требуют нормального распределения данных (хотя бы приблизительно). Зная свойства нормального распределения и изучив внимательно гистограмму, важно определить, являются ли данные нормально распределенными. Теоретически нормальное распределение представляет собой гладкую гистограмму в форме колокола без случайных отклонений. Кривая нормального распределения задается функцией плотности распределения: 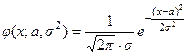 , где a и σ 2 – параметры распределения: a – математическое ожидание; σ 2 – дисперсия данной случайной величины. Для идеального набора нормально распределенных данных такая кривая имеет следующий вид (рис. 3)
, где a и σ 2 – параметры распределения: a – математическое ожидание; σ 2 – дисперсия данной случайной величины. Для идеального набора нормально распределенных данных такая кривая имеет следующий вид (рис. 3)
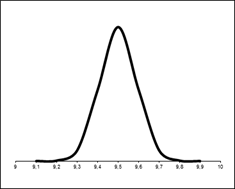 Рисунок 3 – Кривая нормального распределения для идеального набора данных
Как видим, большинство чисел сконцентрировано в средней части диапазона значений (центр колокола a), а оставшиеся значения с затуханием симметрично располагаются по обе стороны от вершины колокола. Величина σ характеризует ширину (масштаб) колокола. Фактически существует много кривых нормального распределения, форма которых напоминает симметричный колокол. Эти кривые отличаются друг от друга расположением центра и масштабом σ. Ниже показаны кривые нормального распределения, построенные в разных масштабах.
Рисунок 3 – Кривая нормального распределения для идеального набора данных
Как видим, большинство чисел сконцентрировано в средней части диапазона значений (центр колокола a), а оставшиеся значения с затуханием симметрично располагаются по обе стороны от вершины колокола. Величина σ характеризует ширину (масштаб) колокола. Фактически существует много кривых нормального распределения, форма которых напоминает симметричный колокол. Эти кривые отличаются друг от друга расположением центра и масштабом σ. Ниже показаны кривые нормального распределения, построенные в разных масштабах.
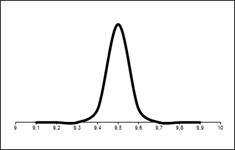 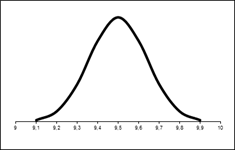 Рисунок 4 – Кривые нормального распределения
Поскольку реальные наборы нормально распределенных данных носят случайный характер, то они не имеют идеальную степень гладкости гистограмм и содержат некоторые случайные отклонения от теоретической кривой.
Рисунок 4 – Кривые нормального распределения
Поскольку реальные наборы нормально распределенных данных носят случайный характер, то они не имеют идеальную степень гладкости гистограмм и содержат некоторые случайные отклонения от теоретической кривой.
|
Б. Вариационные ряды
Исследователь, интересующийся тарифным разрядом рабочих механического цеха, провел опрос 100 рабочих. Расположим наблюдавшиеся значения признака в порядке возрастания. Эта операция называется ранжированием статистических данных. В результате получим следующий ряд, который называется ранжированным:
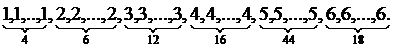
Из ранжированного ряда следует, что исследуемый признак (тарифный разря д ) принял шесть различных значений: 1, 2, 3, 4, 5 и 6.
В дальнейшем различные значения признака будем называть вариантами, а под варьированием – понимать изменение значений признака.
В зависимости от принимаемых признаком значений признаки делятся на дискретно варьирующие и непрерывно варьирующие.
Тарифный разряд – это дискретно варьирующий признак. Число, показывающее, сколько раз встречается вариант х в ряде наблюдений, называется частотой варианта 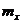 .
.
Вместо частоты варианта х можно рассматривать ее отношение к общему числу наблюдений n, которое называется частостью варианта и обозначается 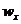 :
:
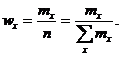 (1.1)
(1.1)
Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом (таблица 3).
Таблица 3 – Дискретный вариационный ряд
| Тарифный разряд, х | Количество рабочих, 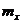
| Доля рабочих, 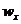
|
| 0,04 | ||
| 0,06 | ||
| 0,12 | ||
| 0,16 | ||
| 0,44 | ||
| 0,18 | ||
| Итого | 1,00 |
Наряду с понятием частоты используют понятие накопленной частоты, которую обозначают 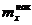 . Накопленная частота показывает, во скольких наблюдениях признак принял значения, меньшие заданного значения х. Отношение накопленной частоты к общему числу наблюдений n, называют накопленной частостью и обозначают
. Накопленная частота показывает, во скольких наблюдениях признак принял значения, меньшие заданного значения х. Отношение накопленной частоты к общему числу наблюдений n, называют накопленной частостью и обозначают 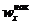 . Очевидно, что
. Очевидно, что
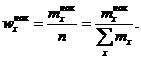 (1.2)
(1.2)
Накопленные частоты (частости) для дискретного вариационного ряда, заданного в таблице 3, вычислены в таблице 4.
Пусть необходимо исследовать выработку на одного рабочего-станоч-ника механического цеха в отчетном году в процентах к предыдущему году. Здесь исследуемым признаком х является выработка в отчетном году в процентах к предыдущему. Это непрерывно варьирующий признак. Для выявления характерных черт варьирования значений признака объединим в группы рабочих, у которых величина выработки колеблется в пределах 10% (всего было опрошено 117 рабочих). Сгруппированные данные представим в таблице 4.
Таблица 4 – Расчет накопленных частот (частостей) для дискретного вариационного ряда
| Х | 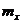
| 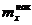
| 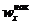
|
| 0,04 | |||
| 4+6=10 | 0,10 | ||
| 10+12=22 | 0,22 | ||
| 22+16=38 | 0,38 | ||
| 38+44=82 | 0,82 | ||
| 82+18=100 | 1,00 | ||
| Итого | -- | -- |
Таблица 5 – Группировка данных исследования выработки на одного рабочего-станочника механического цеха в отчетном году
| Исследуемый признак, Х | Количество рабочих, m | Доля рабочих, w | Накопленная частота,
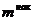
| Накопленная частость,
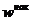
|
| 80-90 | 8/117 | 8/117 | ||
| 90-100 | 15/117 | 8+15=23 | 23/117 | |
| 100-110 | 46/117 | 23+46=69 | 69/117 | |
| 110-120 | 29/117 | 69+29=98 | 98/117 | |
| 120-130 | 13/117 | 98+13=111 | 111/117 | |
| 130-140 | 3/117 | 111+3=114 | 114/117 | |
| 140-150 | 3/117 | 114+3=117 | 117/117=1 | |
| Итого | -- | -- |
В таблице 5 частоты m показывают, во скольких наблюдениях признак принял значения, принадлежащие тому или иному интервалу. Такую частоту называют интервальной, а отношение ее к общему числу наблюдений – интервальной частостью w. Таблицу, позволяющую судить о распределении частот (или частостей) между интервалами варьирования значений признака, называют интервальным вариационным рядом.
В таблице 5 для верхних границ интервалов приведены накопленные частоты (частости) 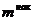 (
(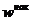 ).
).
Интервальный вариационный ряд строят по данным наблюдений за непрерывно варьирующим признаком, а также за дискретно варьирующим, если велико число наблюдавших вариантов. Дискретный вариационный ряд строят только для дискретно варьирующего признака.
Иногда интервальный вариационный ряд условно заменяют дискретным. Тогда серединное значение интервала принимают за вариант х, а соответствующую интервальную частоту – за 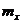 .
.
Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов и в соответствии с ней сгруппировать результаты наблюдений.
Для определения оптимального постоянного интервала h часто используют формулу Стерджесса:
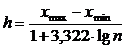 , (1.3)
, (1.3)
где 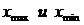 – соответственно максимальный и минимальный значения вариантов.
– соответственно максимальный и минимальный значения вариантов.
Если в результате расчетов h окажется дробным числом, то за величину интервала следует взять либо ближайшее целое число, либо ближайшую несложную дробь.
За начало первого интервала рекомендуется принять величину 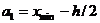 ; начало второго интервала совпадает с концом первого и равно
; начало второго интервала совпадает с концом первого и равно 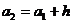 ; начало третьего интервала совпадает с концом второго и равно
; начало третьего интервала совпадает с концом второго и равно 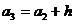 . Построение интервалов продолжается до тех пор, пока начало следующего по порядку интервала не будет больше
. Построение интервалов продолжается до тех пор, пока начало следующего по порядку интервала не будет больше 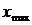 . После установления шкалы интервалов следует сгруппировать результаты наблюдений.
. После установления шкалы интервалов следует сгруппировать результаты наблюдений.
Средние величины
Статистическая средняя величина является обобщенной характеристикой совокупности по определенному признаку. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами, и находят выражение общие, закономерные черты, свойственные всей совокупности явления. Это свойство средних предопределяет использование их в качестве основного метода статистической науки. Заметим, что только для качественно однородных наблюдений имеет смысл вычислять средние величины.
Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или логическую формулу средней (ЛФС):
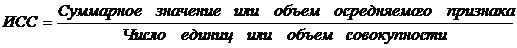
Так, например, для расчета средней урожайности картофеля региона, состоящего из нескольких областей, ИСС представляет собой следующее отношение:
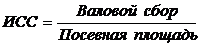
Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней. Если, например, требуется рассчитать средний размер вклада в банке, то ИСС будет следующим:
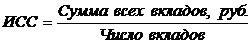
От того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации ИСС потребуется одна из следующих форм средней величины: средняя арифметическая; средняя гармоническая; средняя геометрическая; средняя квадратическая, кубическая и т.д.
Перечисленные средние относятся к степенным средним. Степенной средней q -го порядка  называют такую среднюю, при замене которой каждого наблюдения остается неизменной сумма q -тых степеней наблюдений:
называют такую среднюю, при замене которой каждого наблюдения остается неизменной сумма q -тых степеней наблюдений:
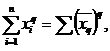 (1.4)
(1.4)
где 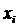 – i -тый вариант усредняемого признака;
– i -тый вариант усредняемого признака;
n – количество наблюдений;
q – положительное или отрицательное целое число.
Из формулы (1.4) получаем выражение для расчета степенной средней q-ого порядка:
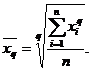 (1.5)
(1.5)
При q = 1 имеем простую среднюю арифметическую (невзвешенную):
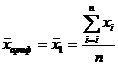 (1.6)
(1.6)
При q = -1 имеем среднюю гармоническую:
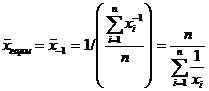 (1.7)
(1.7)
При q = 2 имеет место средняя квадратическая, при q = 3 – средняя кубическая и т.д.
Средней геометрической 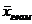 называют корень n -ной степени из произведения значений наблюдений
называют корень n -ной степени из произведения значений наблюдений 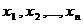 :
:
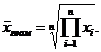 (1.8)
(1.8)
Можно показать, что 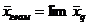
q®0
Наиболее распространенной средней величиной является средняя арифметическая. Простая (невзвешенная) средняя арифметическая рассчитывается по формуле (2.6). Далее среднюю арифметическую величину будем обозначать 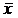 .
.
Если по наблюдениям построен вариационный ряд, то средняя арифметическая величина имеет вид:
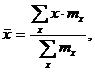 (1.9)
(1.9)
где х – вариант, если ряд дискретный, и центр интервала, если ряд интервальный;
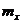 – соответствующая частота;
– соответствующая частота; 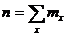 .
.
Частоты 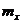 в формуле (2.9) называют весами, операцию умножения х на
в формуле (2.9) называют весами, операцию умножения х на 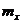 - операцией взвешивания, а среднюю арифметическую, вычисленную по формуле (1.9) – средней арифметической взвешенной.
- операцией взвешивания, а среднюю арифметическую, вычисленную по формуле (1.9) – средней арифметической взвешенной.
Среднюю арифметическую величину для вариационного ряда можно вычислять по формуле:
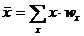 , (1.10)
, (1.10)
которая является следствием формулы (2.9).
Действительно,
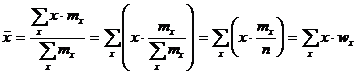
Рассмотрим основные свойства средней арифметической.
Сумма отклонений результатов наблюдений от средней арифметической равна нулю.
Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то средняя арифметическая уменьшится (увеличится) на то же число.
Если все результаты наблюдений уменьшить (увеличить) в одно и тоже число раз, то средняя арифметическая уменьшится (увеличится) во столько же раз.
Если ряд наблюдений состоит из k групп наблюдений, то средняя арифметическая всего ряда 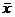 равна взвешенной средней арифметической групповых средних
равна взвешенной средней арифметической групповых средних 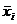 , причем весами являются объемы групп
, причем весами являются объемы групп 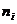 :
:
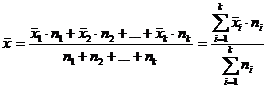 (1.11)
(1.11)
Средняя арифметическая для сумм (разностей) взаимно соответствующих значений признака двух рядов наблюдений с одинаковым числом наблюдений равна сумме (разности) средних арифметических этих рядов:
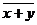 =
= 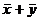 ,
, 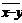 =
= 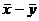 .
.
Следствие. Средняя арифметическая алгебраической суммы соответствующих значений признака нескольких рядов наблюдений равна алгебраической сумме средних арифметических этих рядов.
Известно, что степенные средние разных видов, исчисленные по одной и той же совокупности, имеет различные количественные значения. И чем больше показатель степени, тем больше и величина соответствующей средней:
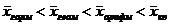 .
.
Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется мажорантностью средних.
Таблица 3.1 - Виды степенных средних и их применение
| m | Название средней | Формула расчета средней | Когда применяется | |
| простая | взвешенная | |||
| Арифметическая | 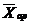 = = 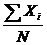 (17) (17)
| 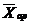 = = 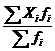 (18) (18)
| Чаще всего, кроме тех случаев, когда должны применяться другие виды средних | |
| –1 | Гармоническая | 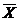 ГМ = ГМ = 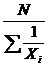 (19) (19)
| 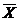 ГМ = ГМ = 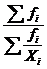 (20) (20)
| Для осреднения величин с дробной размерностью при наличии дополнительных данных по числителю дробной размерности |
| Геометрическая | 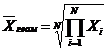 (21) (21)
| 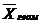 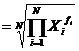 (22) (22)
| Для осреднения цепных индексов динамики | |
| Квадратическая | 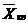 = = 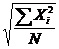 (23) (23)
| 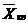 = = 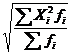 (24) (24)
| Для осреднения вариации признака (расчет средних отклонений) | |
| Кубическая | 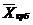 = = 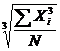 (25) (25)
| 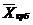 = = 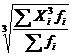 (26) (26)
| Для расчета индексов нищеты населения | |
| Хронологическая | 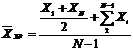 (27) (27)
| 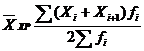 (28) (28)
| Для осреднения моментных статистических величин |
Помимо степенных средних, в статистической практике также используются позиционные средние, среди которых наиболее распространены мода и медиана.
Медианой 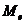 называют значение признака, приходящегося на середину ранжированного ряда наблюдений, если проведено нечетное число наблюдений
называют значение признака, приходящегося на середину ранжированного ряда наблюдений, если проведено нечетное число наблюдений 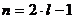 , а результаты наблюдений проранжированы и выписаны в следующий ряд:
, а результаты наблюдений проранжированы и выписаны в следующий ряд:
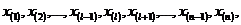
где 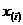 – значение признака, занявшее i -ое порядковое место в ранжированном ряду.
– значение признака, занявшее i -ое порядковое место в ранжированном ряду.
На середину ряда приходится значение 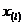 , следовательно
, следовательно 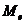 =
= 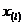 .
.
Если проведено четное число наблюдений n=2×l, то на середину ранжированного ряда 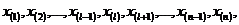 приходятся значения
приходятся значения 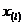 и
и 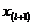 . В этом случае за медиану принимают среднюю арифметическую значений
. В этом случае за медиану принимают среднюю арифметическую значений 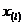 и
и 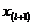 –
– 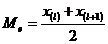 .
.
Для интервального вариационного ряда медиана определяется по формуле:
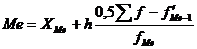 (1.12)
(1.12)
Если в формуле (2.12) числитель и знаменатель входящей в нее дроби разделить на n, то получим другую формулу для расчета 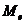 :
:
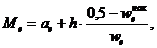 (1.13)
(1.13)
где XMe – нижняя граница медианного интервала;
h – его величина (размах);
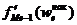 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
– сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
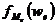 – число наблюдений или объем взвешивающего признака в медианном интервале.
– число наблюдений или объем взвешивающего признака в медианном интервале.
Медианным называется интервал, у которого первый раз накопленная частота (частость) станет равной или более половины всех наблюдений (³ 0,5).
Модой (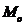 ) называют такое значение признака, которое наблюдалось наибольшее число раз.
) называют такое значение признака, которое наблюдалось наибольшее число раз.
Для дискретного вариационного ряда модой является вариант, которому соответствует наибольшая частота (частость).
В случае интервального вариационного ряда мода вычисляется по следующей формуле:
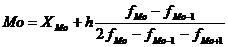 (1.14)
(1.14)
или по тождественной формуле:
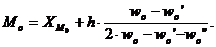 (1.15)
(1.15)
где ХMo – нижнее значение модального интервала, то есть такого, которому соответствует наибольшая частота (частость);
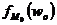 – частота (частость) модального интервала;
– частота (частость) модального интервала;
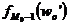 – частота (частость) интервала, предшествующего модальному;
– частота (частость) интервала, предшествующего модальному;