Структурная схема системы с ПИ-регулятором скорости представлена на рис. 23.1. ПИ- регулятор момента с коэффициентом передачи Кп1 и временем изодрома Ти1 представлен на рис.23.1 детализированной структурной схемой. Аналогично представлен ПИ-регулятор скорости с коэффициентом передачи Кп2 и временем изодрома Ти2 Через eps1 и eps2 обозначены ошибки соответственно на входах контуров регулирования момента и скорости. Выходное напряжение uзад(м) регулятора скорости является задающим для подчиненного контура регулирования момента.
 |
Математическая модель системы содержит 5 уравнений состояния
Tпр dw0/dt= - w0 +Kпр uу
Tэ 
= bw0 - M- bw1,
JS 
= M- Mc
= eps1
= eps2,
где к известным переменным состояния, характеризующим энергети-ческую подсистему ЭМС, добавлены выходы интеграторов ПИ-регу-ляторов yp1 и yp2, , характеризующие состояние информационной подсистемы.
Статические и динамические характеристики контура с такими настройками относительно задающего (управляющего) воздействия соответствуют характеристикам стандартной системы, настроенной на симметричный оптимум. Передаточная функция замкнутого контура по управлению имеет вид
,
или
.
При этом
а) Контур не имеет статической и скоростной ошибки, относительно сигнала задания (система обладает астатизмом второго порядка по управлению). В литературе часто такую систему называют двукратно-интегрирующей.
б) Время переходного процесса по управлению составляет величину
tп @ 12Тm2 @ 24Тm1 @ 24Тпр,
однозначно определяется величиной постоянной времени управляемого электрического преобразователя и в 4 раза превышает время переходного процесса в контуре регулирования момента.
|
|
в) Перерегулирование при отработке скачка задания контуром, настроенным на симметричный оптимум, составляет, как известно, величину 43%. Для уменьшения его до величины 8.3% на входе контура, в канале формирования сигнала задания устанавливается фильтр в виде апериодического звена с передаточной функцией
Wф(p)=uзад (p)/ uвх(p)= 1/ (Тфp +1),
причем постоянная времени фильтра выбирается из условия компенсации числителя передаточной функции замкнутой системы, т.е.
Тф= 4 Тm2 @ 8Тm1 @ 8Тпр.
Для учета такого фильтра математическую модель системы следует дополнить еще одним уравнением
Рассмотрим далее характеристики контура относительно возму-щающего воздействия (момента нагрузки Мс)
Преобразуя схему известным образом, получим
w1
Передаточная функция системы по возмущению
Wв(p)= 
или с учетом выражения для коэффициента передачи ПИ-регулятора оптимизированного контура
Кп2 = КмТм b/ Кw4Тпр
Wв(p)= 
Найдем операторное изображение ошибки контура Dw(p) в виде изменения скорости, обусловленного скачкообразным приложением момента статической нагрузки при нулевом задании по скорости и нулевых начальных условиях
Dw(p) = 
Находя установившееся значение ошибки в системе как
,
установим, что эта ошибка равна нулю при любом моменте нагрузки Мс, и следовательно, в пределах зоны пропорциональности УПП механические характеристики определяются выражением
w1=wзад
и по форме не отличаются от аналогичных характеристик одноконтурной системы регулирования скорости с ПИ-регулятором.
|
|
Для оценки характера процесса парирования скачкообразного возмущения определим переходную характеристику системы по возмущению, используя операторное изображение ошибки
Dw(t) = 
Корни полинома знаменателя выражения, заключенного в фигурные скобки, известны:
p1= -1/ 2Tm2=-1/4Tпр;
p2,3= -1/ 4Tm2 ±jÖ3/ 4Tm2=-1/ 8Tпр ±jÖ3/ 8Tпр
Используя формулу разложения, находим
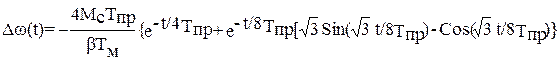(23.1)
График полученной зависимости представлен на рис. 23. 4.
|
Анализ ее показывает, что время парирования возмущения равно времени переходного процесса по управлению, т.е. tп @24 Тпр и вдвое превышает время парирования возмущения в ранее рассмотренной системе с П-регулятором и настройкой на технический оптимум
Для приближенной оценки максимального значения динамического отклонения скорости Dwмакс заметим, что оно имеет место в момент времени t*@6 Тпр. Подставляя значение t* в формулу 23.1, получим
Dwмакс@ Dw(t*)@ 3.54 (Мс/J) Тпр
Настройка контура регулирования скорости на симметричный оптимум широко используется на практике в связи с простотой технической реализации и наличием астатизма первого порядка по возмущению. Однако, как было установлено, перерегулирование при реакции на скачок управляющего воздействия в 10 раз больше, чем в системе, с контуром скорости, настроенным на технический оптимум. Снижение величины перерегулирования без использования входного сглаживающего фильтра и при сохранении астатизма по моменту нагрузки. свойственного двукратноинтегрирующей системе, возможно в трехконтурной системе регулирования скорости.
|
|