Содержание
Введение........................................................................................................... 3
Глава 1. Основные понятия теории полуколец............................................. 4
1.1. Определение полукольца. Примеры.................................................. 4
1.2. Дистрибутивные решетки.................................................................... 5
1.3. Идеалы полуколец............................................................................... 6
Глава 2 Положительные и ограниченные полукольца.................................. 7
2.1. Определение и примеры положительных и ограниченных полуколец 7
2.2. Основные свойства положительных и ограниченных полуколец..... 7
Библиографический список........................................................................... 16
Введение
Теория полуколец – это раздел современной алгебры, обобщающий как кольца, так и дистрибутивные решетки. Понятие полукольца возникло в 30-х годах прошлого столетия. Как самостоятельная теория полукольца начали изучаться в 50-е годы. Особенно интенсивно теория полуколец развивается последние 20 лет, что вызвано не только теоретическим интересом, но и многочисленными ее приложениями.
Целью данной работы является изучение классов положительных и ограниченных полуколец, рассмотрение основных свойств данных алгебраических объектов, часть из которых доказывается автором работы самостоятельно; приведены примеры полуколец.
Работа состоит из 2 глав. В первую главу вошли основные определения и факты, на которые опирается эта работа. Вторая – основная часть всей работы, в ней рассмотрены определения и свойства положительных и ограниченных полуколец, приведены примеры, доказаны некоторые теоремы.
Глава I. «Основные понятия теории полуколец».
Определение полукольца. Примеры.
Определение полукольца: Непустое множество S с бинарными операциями + и · называется полукольцом, если выполняются следующие аксиомы:
1. (S,+) – коммутативная полугруппа с нейтральным элементом 0;
· Ассоциативность: 
;
· Коммутативность: 
;
· Существование нейтрального элемента: 
.
2. (S,·) – полугруппа:
· Ассоциативность: 
;
3. Умножение дистрибутивно относительно сложения:
· левая дистрибутивность: 
а(в+с)=ав+ас;
· правая дистрибутивность: (а+в)с=ас+вс.
4. Мультипликативное свойство0:
· 
.
Эта аксиоматика появилась в 1934 году и ее автором является Вандовер.
Полукольцо S называется коммутативным, если операция 
в нем коммутативна: 
.
Полукольцо S называется полукольцом с единицей, если в нем существует нейтральный элемент по умножению, который называется единицей (1): 
Примеры полуколец:
1. <N,+,·>, где N – множество неотрицательных целых чисел с обычными операциями + и ·;
2. <{0},+,·> - тривиальное полукольцо;
3. Двухэлементные полукольца:< Z2,+,·>, <В,+,·> (в В 1+1=1);
4. Множество матриц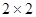 
с элементами из полукольца N и операциями + и ;
5. Множества N, Z, Q+, Q, R+, R и введенных на них различных комбинаций операций: обычные сложение и умножение, максимум 
и минимум 
двух чисел, НОД и НОК, когда они определены.
Полукольцо с импликацией 
называется мультипликативно (аддитивно) сократимым.
Полукольцо, в котором выполняется равенство 
, называется мультипликативно (аддитивно) идемпотентным.
1.2. Дистрибутивные решетки.
Пусть L – произвольное множество. Введем на L отношение 
положив,
.
Отношением порядка называется рефлексивное, транзитивное, антисимметричное бинарное отношение на множестве L, при этом множество L назовем частично упорядоченным множеством.
Отношение на множестве L является отношением порядка.
Пусть M – непустое подмножество частично упорядоченного множества L. Нижней гранью множества M называется такой элемент 
, что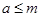 
для любого 
. Нижняя грань m множества M называется точной нижней гранью, если 
, где n – произвольная нижняя грань множества M. Двойственным образом определяется точная верхняя грань.
Частично упорядоченное множество L называется решеткой, если любые два элемента имеют точную верхнюю и точную нижнюю грани; решетка называется дистрибутивной, если в ней выполняются дистрибутивные законы:
Кроме этого определения существует еще одно определение дистрибутивной решетки. Алгебраическая система L с двумя бинарными операциями сложения + и умножения ∙ называется решеткой, если (L, +) и (L,∙) являются идемпотентными коммутативными полугруппами и операции связаны законами поглощения
, 
;
Решетка называется дистрибутивной, если для любых 
, ограниченной, если она имеет 0 и 1.
Идеалы полуколец.
Непустое подмножество I полукольца S называется левым (правым) идеалом полукольца S, если для любых элементов a, b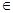 
I, s 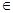S элементы a+b и sa (as) принадлежат I.
Непустое подмножество, являющееся одновременно левым и правым идеалом, называется двусторонним идеалом или просто идеалом полукольца. Идеал, отличный от полукольца S называется собственным. Наименьший из всех (левых) идеалов, содержащий элемент a 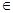S, называется главным (главным левым) идеалом, порожденным элементом a. Обозначается (a) или SaS, односторонние Sa и aS – левый и правый соответственно. Множество всех элементов принадлежащих главному идеалу можно записать так 
.
Собственный идеал M полукольца S называется максимальным (максимальным правым) идеалом, если 
влечет M=A или A=S для каждого идеала A.
Примерами идеалов могут служить следующие подмножества:
1. {0} – нулевой идеал;
2. S – идеал, совпадающий со всем полукольцом;
3. Идеал на полукольце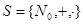 
: 
;
4. Главный идеал ограниченной дистрибутивной решетки L, порожденный элементом a: 
.