Глава 8. Уравнения и неравенства с модулем.
А.
№У8.1) Записать выражение без знака модуля: 
.
№С8.2) Записать выражение без знака модуля: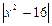 
.
№У8.3) Решить уравнение 
.
№У8.4) Решить уравнение 
.
№У8.5) Найдите сумму корней уравнения 
.
№У8.6) Найти наименьшее целое значение 
, удовлетворяющее неравенству 
.
Ответы к главе 8. №8.1) 
при 
, 
при 
; №8.2) 
при 
, 
при 
; №8.3) 
; №8.4) х= -5,75; -1; 1; 6; №8.5)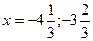 
, сумма = - 8; №8.6) 4.
В.
№У8.7) Найти наибольший целый корень уравнения 
.
№С8.7.1) Решите уравнение: 
.
№У8.7.2) Решить систему неравенств: 
.
№У8.8) Количество целых решений неравенства 
на промежутке 
равно…
№С8.9) Решить неравенство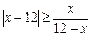 
.
№У8.10) Решить неравенство 
Ответы к главе 8. №8.7) 
, наибольший целый корень =1; №8.7.1) 
; №8.7.2) 
; №8.8) 5; №8.9) 
; №8.10) 
.
Глава 10. Иррациональные уравнения.
А.
№У10.1) Решить уравнение: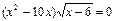 
.
№С10.2) Решить уравнение: 
.
№10.3) Решить уравнение: 
.
№10.4) Решить уравнение: 
.
№У10.5) Решить уравнение 
.
№10.6) Решить уравнение 
.
№С10.7) Решить уравнение 
.
№У10.8) Решить уравнение: 
.
Ответы к главе 10. №10.1) 6; 10; №10.2) 
; 1; №10.3) -6; 0; №10.4) 0; 5; №10.5) -57; №10.6) 55; №10.7) -32; №10.8) 16.
В.
№У10.9) Найти сумму корней уравнения 
.
№С10.10) Найти сумму корней уравнения 
.
№У10.11) Решить уравнение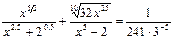 
.
№У10.12) Найдите сумму корней или корень, если он единственный, уравнения 
.
№С10.13) Найдите сумму корней или корень (если он единственный) уравнения: 
.
№У10.14) Решить уравнение 
.
№С10.15) Решить уравнение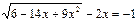 
.
Ответы к главе 10. №10.9) 0,75; №10.10) 
; №10.11) 3; №10.12) 9; №10.13) -2; №10.14) 1; №10.15) 1.
Глава 11. Системы иррациональных уравнений.
В.
№С11.1) Решите систему: 
. В ответ запишите сумму 
, где 
- решение системы.
№У11.2) Решить систему уравнений 
№У11.3) Решить систему уравнений 
№С11.4) Решить систему уравнений 
Ответы к главе 11. №11.1) 97; №11.2) (0; -3,5); (21; 21); №11.3) (3;2); №11.4) (1;2);
|
|
Глава 12. Иррациональные неравенства.
А.
№У12.1) Найдите сумму целых решений неравенства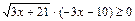 
.
№С12.2) Найти наименьшее целое решение неравенства: 
.
№У12.3) Найти наименьшее целое решение неравенства: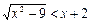 
.
Ответы к главе 12.
№12.1) -22; №12.2) -2; №12.3) 3.
В.
№У12.4) Решить неравенство: 
.
№12.5) Решить неравенство: 
.
№12.6) Решить неравенство: 
.
№12.6.1) Решить неравенство: 
.
№12.7) Решите неравенство 
.
№12.8) Решите неравенство 
.
№У12.9) Решите неравенство 
.
№С12.10) Решите неравенство 
.
№12.11) Решите неравенство 
.
Ответы к главе 12.
№12.4) 
; №12.5)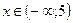 
; №12.6) 
; №12.6.1)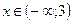 
; №12.7) 
; №12.8) 
; №12.9) 
; №12.10) 
; №12.11) 
.
С.
№У12.12) Решить неравенство: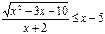 
.
№С12.13) Решить неравенство: 
.
№12.14) Решить неравенство: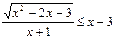 
.
№У12.15) Решить неравенство 
.
Ответы к главе 12.
№12.12) 
; №12.13)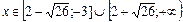 
; №12.14) 
№12.15) 
.
Глава 26. Задачи на движение (по суше, по реке).
В.
№У26.11) Из пункта A в пункт B одновременно вышел пешеход и выехал велосипедист. Пройдя 1/3 пути AB, пешеход сел на мотоцикл и прибыл в пункт B, обогнав велосипедиста на середине пути AB. Если бы пешеход не воспользовался мотоциклом, то до пункта B он добирался бы в два раза дольше. Во сколько раз скорость мотоциклиста больше скорости велосипедиста?
№У26.12) За 80 км до станции назначения поезд был задержан у семафора на 24 минуты. Затем машинист увеличил на 10 км/ч скорость, с которой поезд ехал до остановки, и поэтому поезд прибыл в пункт назначения по расписанию. С какой скоростью ехал поезд после остановки?
№С26.13) Турист на лодке проплыл против течения 10 км и по течению 18 км, затратив на весь путь 4 часа. Скорость течения реки равна 2 км/ч. Определить скорость лодки в стоячей воде (км/ч).
|
|
№С26.14) Лодка в 8.00 вышла из пункта А в пункт В, расположенный в 20км вниз по течению реки. Пробыв в пункте В 30 минут, лодка отправилась назад и вернулась в пункт А в 11.30. Определить в (км/ч) собственную скорость лодки, если скорость течения реки 5км/ч.
№У26.15) Катер прошел 26 км по течению реки и 40 км против течения, затратив на путь по течению на 1 час меньше, чем на путь против течения. Найдите собственную скорость катера, если скорость течения реки 3 км/ч.
Ответы к главе 26. №26.11) в 3 раза; №26.12) 50 км/ч; №26.13) 8 км/ч; №26.14) 15 км/ч; №26.15) 23 км/ч.
С.
№У26.16) Из пунктов А и В выехали одновременно навстречу друг другу велосипедист и мотоциклист. Проехав 1/3 пути между A и B, велосипедист пересел в автомобиль и встретил мотоциклиста на середине пути АВ. Если бы велосипедист пересел в автомобиль, проехав лишь 1/4 часть пути АВ, то он затратил бы времени на путь АВ на 25% меньше, чем мотоциклист из B в A. Во сколько раз скорость автомобиля больше скорости мотоциклиста?
№У26.17) Две автомашины выехали одновременно из пункта A в одном направлении со скоростями 40 км/ч и 50 км/ч. Третья машина выехала из пункта A на полчаса позже и догнала вторую машину через полтора часа после того как обогнала первую машину. Найти скорость третьей машины.
Ответы к главе 26. №26.16) в 
; №26.17) 60км/ч.
Задача недели. №4.20) Найдите сумму квадратов корней уравнения: 
. (НГПУ, 2015, 2016)