Описание решения задач линейного программирования в Excel.
Алгоритмы симплексного метода и метода «branch-and-bound» для решения линейных и целочисленных задач с ограничениями разработаны Джоном Уотсоном (John Watson) и Деном Филстра (Dan Fylstra) из Frontline Systems, Inc.
Средство поиска решения Microsoft Excel использует алгоритм нелинейной оптимизации Generalized Reduced Gradient (GRG2), разработанный Леоном Ласдоном (Leon Lasdon, University of Texas at Austin) и Аланом Уореном (Allan Waren, Cleveland State University).
Поиск решений является частью блока задач, который иногда называют анализ "что - если". Процедура поиска решения позволяет найти оптимальное значение формулы содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках. Чтобы сузить множество значений, используемых в модели, применяются ограничения. Эти ограничения могут ссылаться на другие влияющие ячейки.
Процедуру поиска решения можно использовать для определения значения влияющей ячейки, которое соответствует экстремуму зависимой ячейки — например можно изменить объем планируемого бюджета рекламы и увидеть, как это повлияет на проектируемую сумму расходов.
Решение линейной оптимизационной задачи.
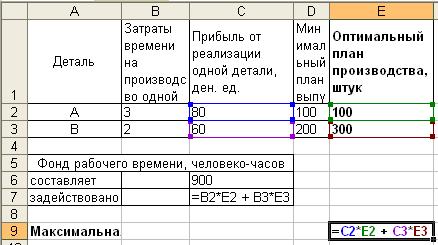
Цех выпускает детали А и В. На производство детали А рабочий тратит 3 часа, на производство детали В - 2 часа. От реализации детали А предприятие получает прибыль 80 ден. ед., В - 60 ден. ед. Цех должен выпустить не менее 100 штук деталей А и не менее 200 штук деталей В. Сколько деталей каждого вида надо выпустить для получения наибольшей прибыли, если фонд рабочего времени составляет 900 человеко-часов.
|
|
Математическая модель задачи.
Обозначим за x1 и x2 количество изделий А и В в оптимальном плане производства.

Решение задачи в MS Excel.
В качестве переменных х1 и х2 будем использовать ячейки E2 и E3 соответственно. Для значения целевой функции будем использовать ячейку E9:
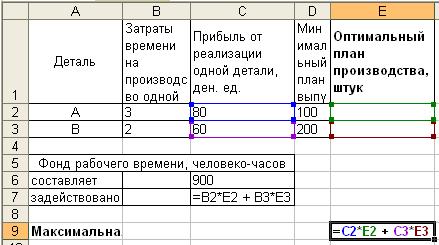
Далее выбираем пункт меню Сервис/Поиск решения:
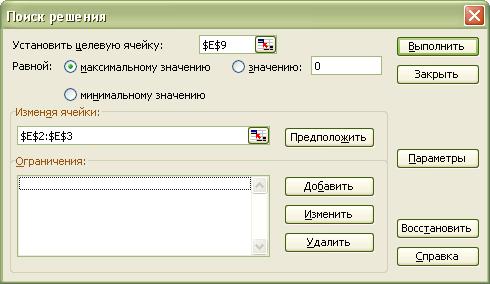
Перед нами открывается диалоговое окно Поиск решения. В нём указываем, что нам необходимо установить ячейку $E$9 максимальному значению, изменяя ячейки $E$2:$E$3. Далее нажимаем кнопку Добавить для добавления ограничений. И добавляем следующие ограничения:
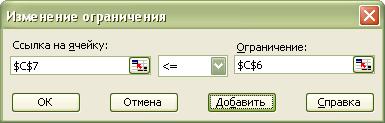
ограничения по фонду рабочего времени
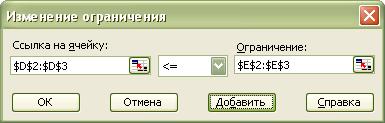
ограничения по минимальному плану производства
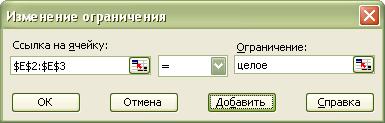
количество изделий должно быть целым числом
После ввода каждого ограничения нажимаем кнопку Добавить. После ввода последнего ограничения нажимаем кнопку OK. И диалоговое окно Поиск решения принимает следующий вид:
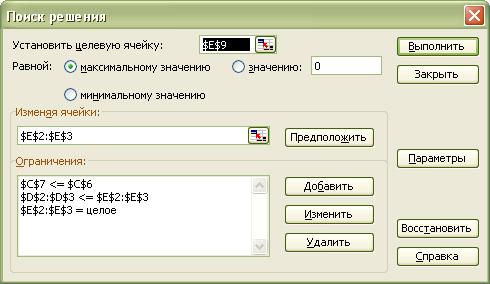
Нажимаем кнопку Выполнить. И перед нами открывается диалоговое окно Результаты поиска решения:
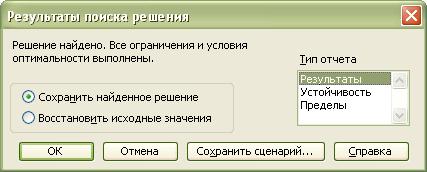
Выбираем создание отчёта по результатам. Отчеты по устойчивости и пределам не создаются при использовании целочисленных ограничений на переменные. После нажатия кнопки OK в рабочей книге появляется новый лист с названием Отчет по результатам 1 содержащий отчёт по результатам, и получаем следующие результаты:
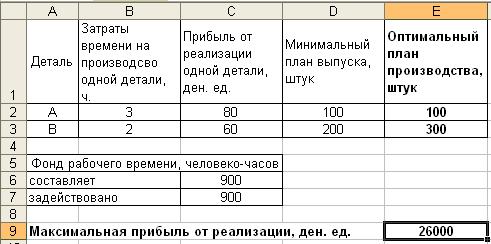
| Деталь | Затраты времени на производсво одной детали, ч. | Прибыль от реализации одной детали, ден. ед. | Минимальный план выпуска, штук | Оптимальный план производства, штук | |||
| А | |||||||
| В | |||||||
| Фонд рабочего времени, человеко-часов | |||||||
| составляет | |||||||
| задействовано | |||||||
| Максимальная прибыль от реализации, ден. ед. | |||||||
|
|
Отчёт по результатам.
| Целевая ячейка (Максимум) | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| $E$9 | Максимальная прибыль от реализации, ден. ед. Оптимальный план производства, штук | |||||
| Изменяемые ячейки | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| $E$2 | А Оптимальный план производства, штук | |||||
| $E$3 | В Оптимальный план производства, штук | |||||
| Ограничения | ||||||
| Ячейка | Имя | Значение | Формула | Статус | Разница | |
| $C$7 | задействовано Прибыль от реализации одной детали, ден. ед. | $C$7<=$C$6 | связанное | |||
| $D$2 | А Минимальный план выпуска, штук | $D$2<=$E$2 | связанное | |||
| $D$3 | В Минимальный план выпуска, штук | $D$3<=$E$3 | не связан. | |||
| $E$2 | А Оптимальный план производства, штук | $E$2=целое | связанное | |||
| $E$3 | В Оптимальный план производства, штук | $E$3=целое | связанное |
Анализ отчета показывает, что фонд рабочего времени задействован на 100%.
|
|
3.2.4. Электронная таблица в режиме формул.
3.2.5. Электронная таблица в режиме значений.