В настоящее время традиционный взгляд на содержание обучения математике, её роль и место в общем образовании пересматривается и уточняется. Для продуктивной деятельности в современном мире требуется достаточно прочная базовая математическая подготовка.
Факультативные занятия по математике призваны углублять математические знания школьников, уже определивших основной круг своих учебных интересов.
Главной целью факультативных занятий по математике является углубление и расширение знаний, развитие интереса учащихся к предмету, развитие их математических способностей, привитие школьникам интереса и вкуса к самостоятельным занятиям математикой, воспитание инициативы и творчества.
Для того, чтобы факультативные занятия по математике были эффективными, необходимо организовать там, где есть:
1) высококвалифицированные учителя или другие специалисты, способные вести занятия на высоком научно – методическом уровне;
2) не менее 15 учащихся, желающих изучать данный факультативный курс. [12]
Факультативы – занятия, основанные на принципе добровольного участия и призванные решать три основные задачи:
1) повышение уровня математического мышления, углубление теоретических знаний и развитие практических навыков учащихся, выявления математических способностей;
2) организация досуга учащихся в свободное от учёбы время.
Данный факультатив предназначен для учеников 11 классов.
Для проведения факультатива выделяется 1 час в неделю, всего 16 часов, разработан на первое полугодие. [18]
По существу, факультативные занятия являются наиболее динамичной разновидностью дифференциации обучения.
6. Тематическое планирование факультатива
| История изучения плоских кривых | 1 ч | |
| Способы образования кривых | 3 ч | |
| Классификация плоских кривых | 4 ч | |
| Алгебраические кривые | 1 ч | |
| Род алгебраических кривых | 2 ч | |
| Трансцендентные кривые | 1 ч | |
| Кривые, изучаемые в школьном курсе математики | 6 ч | |
| Эллипс | 1 ч | |
| Гипербола | 1 ч | |
| Парабола | 2 ч | |
| Итоговое занятие. Выпуск математической газеты | 2 ч |
Занятие №1
Тема: История изучения плоских кривых
Цели: 1) познакомить с историей изучения плоских кривых;
2) развить интерес у учащихся к знаниям, повысить интерес к учению;
3) углубить знания, полученные на уроках математики.
Ход занятия
I. Организационный момент
II. Основная часть
1) Лекция об истории изучения плоских кривых [см. гл. I § 1]
2) Задание
Ребята, разгадаем с вами кроссворд:
ПАС К АЛЬ
ПАПИ Р УС
АПОЛЛОН И Й
РОБЕР В АЛЬ
А РХИМЕД
ГЕОМЕТРИ Я
По горизонтали
1. Учёный, считавший, что дуга спирали Архимеда равна дуге параболы
2. Египтяне за 17–20 веков до нашей эры занимались квадратурой круга. Как назывался документ?
3. Кто написал трактат о конических сечениях? (3–2 в. до н.э.)
4. Какой учёный показал, что задача спрямления спирали идентична задаче спрямления параболы?
5. Учёный, решивший задачу о квадратуре сегмента параболы.
6. Как называлась книга Р. Декарта, изданная в 1637 году?
По вертикали
1. Название линии, прошедшей большой исторический период.
III. Итог занятия
1) Домашнее задание
Написать реферат на тему «История изучения плоских кривых».
Занятие №2–3
Тема: Эллипс
В декартовой системе координат, как хорошо известно, окружность радиуса R c центром C (a; b) задаётся уравнением (x 2 – a 2) + (y 2 – b 2) = R 2. Если сжать окружность с центром в начале координат к вертикальному диаметру с коэффициентом k > 0, то получится линия с уравнением k 2 x 2 + y 2 = R 2 (1), которая называется эллипсом. При этом ясно, что если k > 1, то это действительно сжатие в привычном смысле этого слова (рис. 16, а), а если 0 < k < 1, то это растяжение (рис. 16, б). Но договоримся использовать один общий термин – сжатие.
Преобразуем уравнение (1). Разделим его обе части на R 2:
всегда.
Сделаем замену 
и 
, тогда получим уравнение эллипса в общем виде; 
(2).
Рис. 16
Уравнение (2) называется каноническим уравнением эллипса. В школьном курсе изучается уравнение окружности с центром в начале координат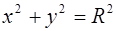 
(3).
Посмотрим, как связаны окружность и эллипс.
В уравнении (3) сделаем замену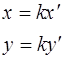 
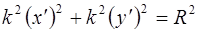Разделим на R 2:
. Пусть , тогда 
.
Итак, мы видим, что окружность – частный случай эллипса, когда а = b.
Отметим ещё, возвращаясь к уравнению (1), что окружность – это эллипс, где k = 1.
Из уравнений видно, что эллипс – линия, симметричная относительно обеих осей координат, а значит, и центрально-симметричная. Геометрически, он полностью характеризуется одним из поперечных размеров (они называются осями эллипса) и их отношением.
Вокруг эллипса естественным образом описывается прямоугольник со сторонами, равными осям эллипса и параллельными координатным прямым, который является результатом сжатия квадрата, описанного вокруг исходной окружности. Называется он осевым прямоугольником эллипса. Если научиться его строить по уравнению эллипса, то довольно легко после этого изобразить и сам эллипс.
1) Например, дано уравнение а) 3 х 2 + у 2 = 7. Изобразить эллипс двумя способами. [16]
I способ
Запишем его в виде 
. Устанавливаем, что 
, строим осевой прямоугольник со сторонами 2 R, l и изображаем сам эллипс (рис. 17). Отметим, что в правой части уравнения должно быть положительное число, а в левой – сумма квадрата абсциссы, взятого с положительным коэффициентом, и квадрата ординаты.
Рис. 17
II способ
Приведём уравнение к каноническому виду.
Разделим обе его части на 7.
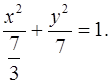
Получим, что 
Строим осевой прямоугольник со сторонами а и 2 b, а затем изображаем эллипс.
Отметим, что, например, уравнение 3 х 2 + 5 у 2 = 7 следует сначала преобразовать к виду х 2 + у 2 = 
или 
а затем находить R, k и a, b соответственно.
Если центр эллипса находится не в начале координат, но его оси параллельны координатным осям, то он задаётся уравнением 
(4),
где С (а; b) – центр эллипса. Это легко следует из формул параллельного переноса, или каноническим уравнением
(5) – С (х; у) – центр эллипса.
Данного материала достаточно для построения эллипса в том случае, если он задан уравнением, содержащем как квадраты, так и первые степени переменных.
б) 
I способ
Преобразуем к виду (4): 
Это уравнение эллипса с центром в точке С (5; – 4), где k = 
(рис. 18)
Рис. 18
II способ
Преобразуем к виду (5):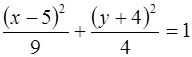 
. Получили уравнение эллипса с центром в точке С (5; – 4), где а = 3, b = 2.
Строим сам эллипс.
2. Найти длины полуосей и координаты фокусов следующих эллипсов:
а) 
Приводим уравнение к каноническому виду 
, а = 3, b = 2.
Фокусы F 1 и F 2 имеют координаты F 1(с; 0) и F 2(– с; 0).
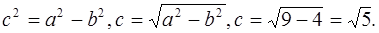
Итак, F 1(
; 0) и F 2(
; 0) а = 3, b = 2.
б) 
Решаем аналогично а). 
, а = 3, b = 1.
F 1(с; 0), F 2(– с; 0). 
Итак, F 1(
; 0) и F 2(
; 0) а = 3, b = 1.
в) 
, а = 
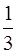, b = 
.
F 1(с; 0), F 2(– с; 0): 
Итак, а = 
, b = 
, F 1(
; 0), F 2(- 
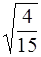; 0).
3. Найти координаты точек М, принадлежащих эллипсу 
и равноудалённых от фокусов.
Пусть М (х; у), тогда МF 1 = МF 2 (по условию). Т. к. F 1(с; 0), F 2(– с; 0): 
то 
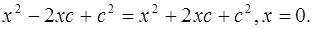
Если х = 0, то, подставляя его в исходное уравнение, получим: 
, 
Следовательно, 
и 
.
4. Взяв на плоскости прямоугольную декартову систему координат, изобразить области, определяемые следующими системами неравенств.
а) 
Построим множество точек, определяемых 1-м, 2-м, 3-м неравенством.
Найдём пересечение этих множеств.
I. Построим эллипс 
но т. к. неравенство строгое, то точки эллипса не принадлежат искомой области, т.е. неравенство (2) задаёт внутренние точки эллипса.
Устанавливаем, что R = 3,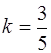 
(0< k <1), 
Cтроим осевой прямоугольник со сторонами 
и изображаем эллипс.
II. Строим множество точек, заданных вторым неравенством. Для этого строим прямую 
и штрихуем определяемую область.
III. Аналогичные рассуждения для построения области, заданной неравенством у + 2 > 0.
Построение.
б) 
Построим множество точек, определяемых 1-м, 2-м, и 3-м неравенствами.
Найдём пересечение этих множеств.
I. 
– эллипс, точки которого не принадлежат искомой области (неравенство строгое), т.е. неравенство задаёт внешние точки эллипса. Приведём уравнение к каноническому виду
Строим осевой прямоугольник со сторонами a и b, изображаем эллипс.
II. Строим множество точек, заданных неравенством (2). Для этого изображаем прямую у = 3 и штрихуем определяемую область.
III. Рассуждаем аналогично.
Построение.
Занятие №4–5
Тема: Гипербола
Учащиеся хорошо знакомы с гиперболой как с графиком функции 
и с такими понятиями, как её ветви и асимптоты. Гипербола не только является центрально-симметричной линией (как график нечётной функции), но и имеет две оси симметрии – это биссектрисы пар вертикальных координатных углов (рис. 19).
Рассмотрим уравнение x 2 – y 2 = l и покажем, что линия, задаваемая им – это тоже гипербола. Перепишем уравнение в виде (x – y) (x + y) = l. Введём новые переменные: 
тогда в системе (u, v) исходное уравнение примет вид uv = l, и это будет гипербола, расположение ветвей которой полностью определяется знаком числа l.
Для изображения гиперболы выясним, как расположены оси системы координат (u, v) в координатной плоскости (х, у), считая, что u – абсцисса и v – ордината в новой системе координат. Ось абсцисс – это множество точек, для которых v = 0, т.е. 
в исходной системе координат, или в исходной системе координат, или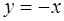 
. Это биссектриса чётных координат углов. Аналогично, 
. Это биссектриса нечётных координатных углов. Для выяснения направлений на осях рассмотрим на оси Ou точку А (рис. 20), которая в системе координат (х, у) имеет координаты (1, -1). Тогда для этой точки u = 1 – (– 1) = 2 > 0, т.е. она лежит на положительной полуоси Оu. Аналогично, рассматривая на оси Ov точку В (1; – 1), получим, что для неё 
, и, значит, она расположена на положительной полуоси Ov.
Это позволяет сделать вывод о том, что преобразование переводит систему координат (х, у) в систему (u, v), оси которой повёрнуты пол отношению к исходной на угол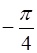 
.
Рис. 19
Рис. 20
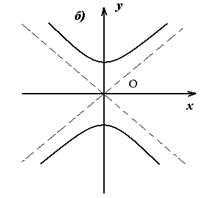
Рис. 21
Уравнение при этом преобразуется в уравнение uv = l, которое равносильно уравнению 
ибо 
равенство означало бы 
, и, значит, 
В зависимости от знака числа l мы можем изобразить ветви гиперболы в соответствующих координатных четвертях системы 
, тем самым будет получено изображение гиперболы, задаваемой уравнением 
в системе координат 
.
При этом, подставляя в исходное уравнение 
или 
в зависимости от знака l, мы получим точки пересечения гиперболы с той или иной координатной осью. Эти точки называются вершинами гиперболы (рис. 21).
Если к гиперболе 
провести касательные в её вершинах (Теорема. Касательная к гиперболе в произвольной её точке является биссектрисой внутреннего угла М 0 треугольника F 1 M 0 F 2, имеющего своими вершинами фокусы гиперболы и данную точку М 0, см. рис. 27), то они пересекут асимптоты гиперболы в точках, которые будут вершинами квадрата (это следует из соображений симметрии). Удобно этот квадрат назвать осевым квадратом гиперболы (рис. 23). Центр этого квадрата совпадает с центром симметрии гиперболы, её диагонали – это её асимптоты, а сторона равна 
.
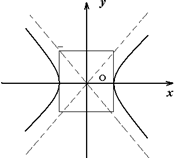
Рис. 22, 23
Если произвести сжатие к оси Ох с коэффициентом k > 0, k ¹ 1, то гипербола преобразуется в линию, также называемую гиперболой, но о такой гиперболе говорят, что она неравнобокая. Исходную же гиперболу называют равнобокой. Прн сжатии осевой квадрат преобразуется в осевой прямоугольник, а диагонали квадрата – в диагонали прямоугольника (они будут асимптотами для получающейся неравнобокой гиперболы). Уравнение неравнобокой гиперболы имеет вид: 
, где k 2 ¹ 1.
Рис. 24
Таким образом, уравнение 
(k ¹ 0, l ¹ 0) всегда задаёт гиперболу. Она равнобокая, если k = 1 и неравнобокая, если k = -1. Её вершины лежат на оси Ох, если l > 0, и на оси Оу, если l < 0. Для её изображения нужно сначала построить осевой прямоугольник, его диагонали и вершины гиперболы (рис. 24).
Преобразуем уравнение 
. Разделим обе его части на l:
(1)
Если l > 0, то уравнение примет вид (1), а если
l < 0 –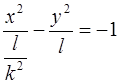 
(2).
Сделаем замену 
, 
, тогда получим уравнение гиперболы в общем виде
(3) 
(4).
Уравнения (3) и (4) называются каноническими уравнениями, а гиперболы, заданные этими уравнениями, называются сопряжёнными, а и b – стороны осевого прямоугольника. Если a = b – осевого квадрата.
Для закрепления решим несколько задач. [17]
1) Построить графики.
а) 
I способ.
Это уравнение равносильно уравнению 
. Поскольку l < 0, то вершины гиперболы расположены на оси Оу. Гипербола неравнобокая, т. к. 
. Строим осевой прямоугольник со сторонами 
и 
, где 
, 
. Чертим график гиперболы.
II. способ
Приведём уравнение к каноническому виду
, 
, следовательно, 
Строим осевой прямоугольник, а затем изображаем гиперболу.
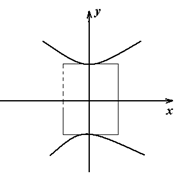
Параллельный перенос гиперболы преобразует уравнение к виду:
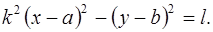(5) (или 
(6)).
Рассмотрим способ построения гиперболы по уравнению данного вида.
б) 
. Преобразуем его к виду (5) 
и далее: 
Это уравнение гиперболы, где 
Осевой прямоугольник со сторонами 
смещён на две единицы вверх и вправо. Строим его и изображаем гиперболу.
II способ.
Приводим уравнение к каноническому виду:
, следовательно, 
Центр осевого прямоугольника – точка (2; 2).
Строим его и изображаем гиперболу.
2) Найти длины полуосей и координаты фокусов следующих гипербол:
а) 
.
Привели к каноническому виду, а следовательно а = 2, b = 3.
F 1 и F 2 имеют координаты: F 1(– с; 0), F 2(с; 0).
Таким образом, F 1(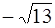
; 0), F 1(
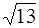; 0).
Ответ: а = 2, b = 3, F 1(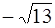; 0), F 1(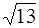; 0).
б) 
Используя каноническое уравнение, получим:
.
Мы знаем, что F 1(– с; 0), F 2(с; 0),
Итак, 
, F 1(
; 0), F 1(
; 0).
в) 
, 
F 1(– с; 0), F 2(с; 0):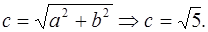 
Ответ: 
F 1(
; 0), F 1(
; 0).
3) Составить каноническое уравнение гиперболы, если расстояние между вершинами равно 8, а расстояние между фокусами равно 10;
Итак, нам дано, что 
Находим, что 
.
Каноническое уравнение гиперболы имеет вид 
Т. к. 
, то уравнение можно записать следующим образом: 
4) Взяв на плоскости прямоугольную декартову систему координат, построить области, определяемые следующими системами неравенств:
а) 
построим множество точек, определяемых 1-м и 2-м неравенствами. Найдём пересечение этих множеств.
I. Построим гиперболу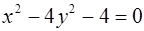 
. После преобразования получаем каноническое уравнение 
с полуосями а = 2 и b = 1. Точки гиперболы не принадлежат искомой области, т. к. неравенство строгое. Это неравенство определяет внутренние точки гиперболы. Строим осевой прямоугольник, гиперболу и изображаем искомую область.
II. Строим множество точек. Заданных вторым неравенством. Для этого изображаем прямую 
и штрихуем определяемую область.
Построение.
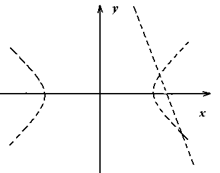
б)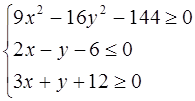 
Построим множество точек, определяемых 1-м, 2-м. 3-м неравенствами. Найдём пересечение этих множеств.
I. построим гиперболу 
. Её точки принадлежат искомой области, т. к. неравенство не строгое. Т. о. Неравенство определяет внешние точки гиперболы. Преобразуем уравнение. 
это уравнение гиперболы, где 
, точки которой не принадлежат искомой области (неравенство строгое), 
строим осевой прямоугольник со сторонами 
и изображаем гиперболу.
II. Строим множество точек, заданных вторым неравенством. Для этого изображаем прямую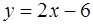 
и штрихуем определяемую область.
III. Рассуждаем аналогично. строим прямую 
и штрихуем определяемую область.
Построение.
Эксперимент
Некоторые практические материалы. Предложенные в гл. II проверены экспериментально в 10–11 классах ГОУ СОШ с. Новкус-Артезиан.
Тема эксперимента: «Различные уравнения эллипса, гиперболы, параболы и их графики».
Эксперимент проводился в два этапа.
I этап эксперимента.
До изложения теории о линиях второго порядка (до Темы 1) предлагались задания на проверку уровня знаний учащихся о знакомых им линиях второго порядка.
Учащимся было предложено ответить на вопросы и выполнить задания:
1. Какие из перечисленных ниже графиков представлены на чертеже:
а) окружность;
б) эллипс;
в) гипербола;
г) парабола?
2. Каким из перечисленных выше уравнений задаётся каждый из них:
а) 
,
б)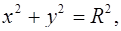 
в)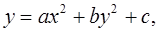 
г) 
3. Какие методы построения графиков функции вы знаете?
4. Приведите примеры распространения линий второго порядка в жизни, природе, технике.
5. Какие вы знаете свойства эллипса, гиперболы, параболы, окружности?
II этап поискового эксперимента проводился после проведения факультативных занятий.
Подбирались задачи, аналогичные тем, которые рассматривались на кружковых занятиях. Задания достаточно стандартные, аналогичные тем, которые были проведены на первом этапе эксперимента и задания по нестандартному решению задач.
Учащимся были предложены следующие задания:
1. Нарисовать схематически графики данных уравнений:
а)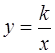 
,
б) 
в)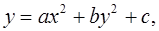 
г) 
.
2. По заданным уравнениям определите название линии второго порядка:
а) 
б)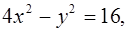 
в) 
г) 
.
3. Построить график функции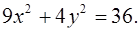 
4. Решить уравнения: а) 
б)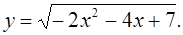 
После проведения эксперимента можно сделать следующий вывод: у учащихся экспериментальной группы значительно поднимается уровень логического мышления и развивается математическая интуиция, они чётко аргументируют ответы, приводят доказательства и хорошо ориентируются в изученном материале, применяя его на уроках.
Результаты эксперимента
| Количество учащихся | I этап | II этап |
| 28% | 75% |
Заключение
В квалификационной работе разработана теория плоских кривых и замечательных кривых, предложена разработка факультатива для учащихся 9–11 классов на тему «Плоские кривые».
После изучения научной и методической литературы материал отобран с учётом психологических и физиологических особенностей учащихся старших классов и систематизирован для целостного изложения.
Выдвинутая гипотеза, на наш взгляд подтверждается на основе наблюдений и частичного эксперимента в период педагогической практики.
Содержание всех занятий позволяет углубить представление учащихся об эллипсе, гиперболе. Параболе и ознакомить их с некоторыми, наиболее часто встречающимися замечательными кривыми, приблизить их к пониманию некоторых важных идей современной математики.
Литература
1. Савелов А.А. Плоские кривые. – М.: ГИФ-МЛ, 1960
2. Гильберт Д., Кон-Фостен С. Наглядная геометрия. – М.: Наука, 1981.
3. Моденов П.С. Аналитическая геометрия М.: Наука, 1969
4. Атанасян Л.С., Базылев В.Т. Геометрия. – учебное пособие для студентов физ. – мат. факультетов пед. институтов. – М.: Просвещение, 1987
5. Александров П.С. Лекции по аналитической геометрии, пополненные необходимыми сведениями из алгебры с приложениями собрания задач, снабжённых решениями, составленные А.С. Пархоменко. – М.: Наука, 1968
6. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1979
7. Энциклопедический словарь юного математика. М.: Педагогика, 1989
8. Математический энциклопедический словарь. М.: Советская энциклопедия, 1988
9. Маркушевич А.И. Замечательные кривые. – М.: – наука, 1978
10. Водинчар М.И., Лайкова Г.А., Калинова Т.Ю. Линии второго порядка и графики иррациональных функций // Математика в школе, 1999, №3.
11. Дубровин В.А., Новиков С.П., Фоменко А.Г. Современная геометрия. Методы и приложения. – М. Наука, 1986
12. Методика преподавания математики в средней школе. – М.: Просвещение, 1980
13. Кузнецова Г.Б. Алгебра точек параболы // Математика в школе, 1974, №2
14. Ткаченко А.А. Об одном свойстве гиперболы // Математика в школе, 1976, №2
15. Лабораторные и практические работы по методике преподавания математики: учебное пособие для физ. – мат. Специальностей пед. институтов \ под редакцией Лященко Е.И. – М., 1988
16. Шарыгин И.Ф. Факультативный курс по математике: решение задач. Уч. пособие для 10 кл. средней школы. – М., 1989
17. Абрамов А.Щ., Ивлев Б.М. и др. Задачи повышенной трудности по алгебре и началам анализа: уч. пособие для 10–11 кл. средней школы. – М., 1993
18. Программа общеобразовательных учреждений. Математика. – М. «Просвещение», 2002