Основные понятия.
1.1.1. Определение. Рациональной дробью (или дробно - рациональнойфункцией) называется функция, равная отношению двух многочленов: ¦ (x)= 
, где Pm (x) - многочлен степени n, Qm (x) - многочлен степени m. При этом Pn (x) называется числителем дроби, а Qm (x) - её знаменателем.
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, то есть m < n; в противном случае (то есть если m ³ n) рациональная дробь называется неправильной.
1.1.2. Теорема. Всякую неправильную дробь можно представить в виде суммы некоторого многочленa ¦ (x) и правильной рациональной дроби 
:
= ¦ (x)+
1.1.2. Правило: Для того, чтобы представить неправильную дроб ь в виде суммы многочлена и правильной дроби, достаточно разделить числитель Pm (x) на знаменатель Qn (x) с остатком: Pm (x)= ¦ (x) Qm (x)+ Rk (x) Тогда (неполное) частное от деления является многочленом ¦ (x), а остаток Rk (x) - числителем правильной дроби .
1.1.3. Упражнение. Представить в виде суммы многочлена и правильной дроби дробь:
a) 
б) 
;
в) 
.
Решение. a) Разделим с остатком числитель 3 x 4-2 x 3+ x 2- x -1 на знаменатель x 2-3: 3 x 4-2 x 3+ x 2- x -1=(x 2-3)(3 x 2-2 х +10)+(-7 х +29) (см. 1.2.2 предыдущего параграфа). Поэтому =3 x 2-2 х +10+ 
.
Ответ: а) =3 x 2-2 х +10+ .
1.1.4. Определение. Правильные рациональные дроби вида 
,, 
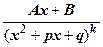, где p 2-4 q <0, A, B, a, p, q - действительные числа, называются простейшими рациональными дробями.
1.1.5. Теорема. Всякую правильную рациональную дробь , знаменатель которой разложен на множители
можно представить единственным образом в виде суммы простейших дробей:
= 
+ 
+…+ 
+ 
+ 
+…+ 
+…+
+ 
+ 
+…+ 
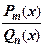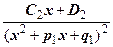+…+ (1.1.1)
+ 
+ 
+…+ 
.
где А 1, А 2, …, B 1, B 2, …, C 1, C 2, …, D 1, D 2, …, M 1, M 2, …, N 1, N 2, …, - некоторые действительные числа.
Например
= 
+ 
+ 
,
= 
+ 
+ 
+ 
,
= 
+ 
+
+ 
+ 
+ 
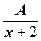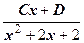Здесь действительные коэффициенты A, B, C, D, E, F, G, H требуют вычислений.
Для нахождения неопределённых коэффициентов А 1, А 2, …, B 1, B 2, …, C 1, C 2, …, D 1, D 2, …, M 1, M 2, …, N 1, N 2, …, в равенстве (1.1.1) можно применить, например, метод неопределённых коэффициентов, который заключается в следующем:
1. Правую часть равенства (1.1.1) приведём к общему знаменателю Qn (x); в результате получим тождество 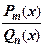º 
, где S (x) - многочлен неопределёнными коэффициентами.
2. Так как в полученном равенстве (тождестве) знаменатели равны, то равны (тождественно) и числители, то есть равны многочлены, стоящие в числителях дробей равенства: Pm (x)= S (x).
3. Так как многочлены равны тогда и только тогда, когда равны соответствующие коэффициенты (см. 1.1.4), то, приравняв коэффициенты при одинаковых степенях в обеих частях равенства Pm (x)= S (x), получим систему линейных уравнений, из которой определяются искомые коэффициенты А 1, А 2, …, B 1, B 2, …, C 1, C 2, …, D 1, D 2, …, M 1, M 2, …, N 1, N 2, …,.
1.1.6. Упражнение. Представить дробь в виде суммы простейших:
a) ; б) ;
в) ; в) 
;
Решение. а) Имеем = 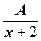+ + . Правую часть этого равенства приведём к общему знаменателю:
= 
=
= 
=
= 
.
Так как в полученном равенстве (тождестве) знаменатели равны, то равны (тождественно) и числители, то есть равны многочлены, стоящие в числителях дробей равенства: х -1=(A + C) x 2+(3 A + B +4 C) x +(2 A + B +4 C). Так как многочлены равны тогда и только тогда, когда равны соответствующие коэффициенты, то, приравняв коэффициенты при одинаковых степенях в обеих частях полученного равенства, получим систему линейных уравнений:
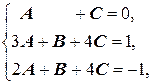
решая которую, например, методом Гаусса, определяем искомые коэффициенты А, В, С:
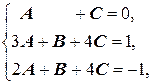Û 
Û Û
Û 
Û 
Таким образом, = 
+ 
- 
.
Ответ: = + - .
1.1.7. Теорема. Всякую рациональную дробь можно представить в виде суммы некоторого многочлена (возможно, нулевого) и простейших дробей.
1.1.8. Упражнение. Представить дробь в виде суммы многочлена и простейших дробей.
a)
б) ;
в) .
Решение. a) Представим сначала дробь в виде суммы некоторого многочлена и правильной рациональной дроби: (см. решение упражнения 1.1.3 а)) =3 x 2-2 х +10+ . Теперь достаточно представить дробь в виде суммы простейших:
= 
= 
+ 
= 
=
= 
;
Û 
Û 
= 
- 
.
Окончательно имеем
=3 x 2-2 х +10+ - .
Ответ: а) =3 x 2-2 х +10+
+ - .